Indexed In
- Genamics JournalSeek
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Publons
- Euro Pub
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Research Article - (2024) Volume 13, Issue 4
Vertical Meaning: Introducing and Exercising Interpersonal Data in Quantum Circuits via Japanese Honorifics
Ryder Dale Walton*Received: 26-Jun-2024, Manuscript No. SIEC-24-26113; Editor assigned: 28-Jun-2024, Pre QC No. SIEC-24-26113 (PQ); Reviewed: 15-Jul-2024, QC No. SIEC-24-26113; Revised: 24-Jul-2024, Manuscript No. SIEC-24-26113 (R); Published: 02-Aug-2024, DOI: 10.35248/2090-4908.24.13.379
Abstract
This paper proposes a novel concept within Quantum Natural Language Processing (QNLP) to encode the interpersonal metafunction of Systemic Functional Linguistics (SFL), particularly tenor, into quantum circuits by treating Japanese honorifics seriously. Because of English language bias in the literature, the incorporation of nuanced aspects of interpersonal communication evident in low-resource languages like Japanese remains underdeveloped and overlooked. This study leverages the quantum computing Python package lambeq to capture grammar and social context specifically, the roles and relationships that define interpersonal interactions in quantum circuits. The newly introduced honorific type h accomplishes this end. This strategy exposes the capability of quantum circuits to model the complex structures of language, moving beyond grammar the horizontal, textual dimension of SFL to embrace the vertical, hierarchical dimension of human communication and social interaction more broadly. Through this lens, the paper underscores the potential of QNLP to transcend traditional linguistic analysis, advocating for a broader and more nuanced understanding of language that includes both the spoken word and the interlocutors’ social persona. An algorithm for parsing Japanese grammar into pre-group diagrams containing the h type is introduced along with a codebase for other researchers to use and to which to contribute. Lastly, a binary classification experiment demonstrates that the circuits generated from these pre-group diagrams are suitable for Quantum Machine Learning (QML) applications.
Keywords
Quantum Natural Language Processing (QNLP); Systemic Functional Linguistics (SFL); Japanese honorifics; Interpersonal metafunction; lambeq; Pre-group grammar; Quantum Machine Learning (QML)
Introduction
What kinds of linguistic information can quantum circuits encode? This preliminary study demonstrates the relevance of that question. The path to an answer begins with Systemic Functional Linguistics (SFL), a theory positing that language operates on multiple levels, including the ideational, textual, and interpersonal [1]. The interpersonal metafunction underscores how language acts as a tool for speakers to negotiate social roles and relationships a language dimension richly encoded in the honorific systems of languages like Japanese [2]. The core of this paper is an endeavor to encode the interpersonal metafunction of SFL into quantum circuits for the first time using the nuanced system of Japanese honorifics. This initiative is motivated by the significant English language bias in current Natural Language Processing (NLP) and Quantum Natural Language Processing (QNLP) literature. This bias obfuscates the rich and implicit interpersonal nuances commonly found in high-context languages like Japanese [3].
This study, then, leverages lambeq to encode the interpersonal metafunction into quantum circuits and utilizes those circuits in a binary classification experiment to show their utility [4,5].
This study is also an invitation to reassess the possibilities of QNLP, urging the field to study language in its entirety. Through an introductory-level and technical examination of Japanese honorifics within a quantum computational framework, this study identifies a path toward a more inclusive, nuanced, and profound understanding of language that examines the interpersonal as much as the textual and informational.
Why take a quantum approach to language?
QNLP aims to leverage the peculiarities of quantum mechanics to unravel the intricate tapestry of human language. It provides a means to encode grammatical and semantic relationships between words or between sentences, depending on the level of granularity, directly into quantum circuits [6,7]. This encoding is made possible by working with variations of monoidal categories, abstractions of vector spaces, the unifying mathematical structure shared by language and quantum mechanics [8]. Then, the reason for taking a quantum approach to language is not strictly about performance, though computing vector spaces is more efficient on quantum hardware [9]. Rather, the quantum advantage provided by QNLP over traditional NLP is the unique ability of the quantum approach to create grammar-aware models using pre-group or CCG (Combinatory Categorical Grammar) grammars [10,11]. Simply put, the QNLP approach specifies grammar as a part of its model, while traditional NLP approaches ignore it. This difference could lead to more consistent and verifiable outputs than contemporary Large Language Models (LLMs).
Contributions and their avenues for further research
This paper provides several novel contributions to further the field and opens the path to further research focused on each contribution as well:
• First, it proposes using the custom atomic type definition functionality of lambeq to encode honorifics as a unique type instead of lumping them in with nouns [12]. Introducing the h type invites further research into other potential types for the more intricate features of Japanese honorifics and particles, as theorized in Walton. [13].
• Second, a binary classification experiment leverages the h type, encouraging future experiments.
• Third, it provides an alternative starting point for other researchers to build their Japanese experiments without relying on the depCCG parser. The source code is available on GitHub [14].
• Fourth, it invites researchers and developers to consider language bias and attempt to mitigate it. Considering overlooked information encoded in quantum circuits is a significant area for further research.
• Lastly, it introduces a simple model based on Japanese honorifics for considering language content across two dimensions: The textual and the interpersonal. Applying more mathematical rigor to this model to present it as a conceptual space a geometric representation of an abstract idea is one avenue for further research. Extending the model to account for the experiential metafunction of SFL is also a worthy endeavor [15].
Background
The nature of QNLP studies is highly interdisciplinary. A brief discussion of work in this field, SFL, and Japanese honorifics sets the context specific to this work.
A brief literature review
This paper situates its contributions within the broader context of ongoing research in QNLP, drawing connections to previous work that has explored the encoding of linguistic structures within quantum circuits to various ends. An in-depth discussion of these findings would be lengthy, so curious readers are encouraged to read the sources and more extensive literature reviews for a more in- depth introduction to the field [16,17]. There has been a great deal of work on diagrammatic reasoning using DisCoCat (Distributional Compositional Categorical), DisCoCirc (Distributional Compositional Circuits) (or “text circuits”), internal wirings, ZX- calculus, and more [18-26]. Diagrammatic reasoning leverages pre- group grammar, category theory, and Frobenius algebras as the mathematical basis of the diagrams as well as the underpinning of the more extensive compositional nature of both discourse and nature [27-34]. This mathematical basis demonstrates a connection between simulating nature and understanding grammar [35-37]. Additionally, researchers have created algorithms and software packages, like lambeq, that support research and experimentation using these ideas [38]. Studies document several different linguistic phenomena in detail, such as hyponymy, entailment, logical and conversational negation, worldly context, representing relative pronouns, and parsing conjunctions [39-43]. Machine learning classification, machine translation, and other intelligence models have also been the subject of ongoing research [44-48]. Lastly, creatives have even applied QNLP in music and computer vision [49,50]. The ideas presented here are indebted to the research cited above.
Inspirations for the h type and for applying QNLP to the Japanese language specifically
First of all, the outstanding work cited here, two papers deserve thanks for inspiring the insights of this study. First, in “Talking Space: Inference from Spatial, Linguistic Meanings”, Wang- Maścianica and Coecke demonstrated that DisCoCat diagrams could encode spatial meaning and arbitrarily defined conceptual spaces. The idea that DisCoCat diagrams can encode more than textual grammar and semantics is the primary inspiration for exploring the h type to encode interpersonal meaning. Second, Liu et al., further developed DisCoCirc, also called text circuits, setting the stage for implementing these circuits in software [51-53]. For the present study, the critical insight from Liu et al., is that text circuit simplification in English strips away the copula “is”. One cannot strip the copula during simplification without truncating interpersonal meaning in a language like Japanese because it carries unique, honorific information. Applying the principles of QNLP to the Japanese language reveals this potential problem. The ideas inspired by those two works taken together are keys to understanding the contributions offered in the present study.
Materials and Methods
Systemic Functional Linguistics (SFL)
The QNLP literature prior to this paper lacks any exploration into SFL. SFL presents language as a multi-faceted model that emphasizes languages as semiotic systems it is a functional tool couched within a social context and relationships that inform the choice network available to interlocutors [54]. SFL relies on the concept of metafunction, which are the foundational aspects of language. Figure 1 provides a graphical representation of SFL, its metafunction, and their components [53].
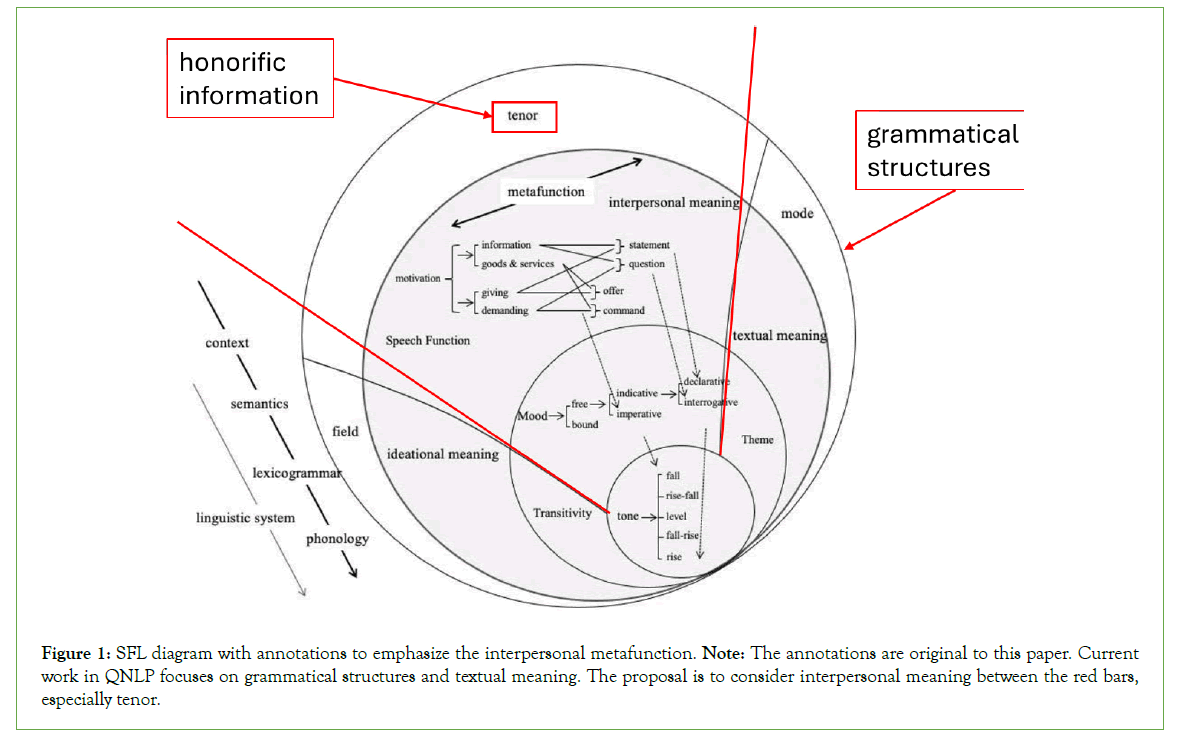
Figure 1: SFL diagram with annotations to emphasize the interpersonal metafunction. Note: The annotations are original to this paper. Current work in QNLP focuses on grammatical structures and textual meaning. The proposal is to consider interpersonal meaning between the red bars, especially tenor.
The three metafunctions are the ideational, textual, and interpersonal. The ideational metafunction is concerned with the representation of reality in language. It includes experiential and logical functions that inform the ideas interlocuters express about the world around them and their inner thoughts. The textual metafunction, on the other hand, is concerned with how words, sentences, and paragraphs are made into meaningful texts as opposed to being long strings of incomprehensible symbols. While these metafunctions are crucial to understanding SFL, the interpersonal metafunction is vital here [54].
The interpersonal metafunction of SFL is broad and covers ideas such as mood, motivation, and the relationship between the interlocutors [55]. The tenor of the discourse conveys the latter idea.
More completely, tenor is concerned with the identity of the interlocutors, their roles, their relationship or intimacy with one another, and their positions within their societal context [56]. The Japanese honorific system, which includes different grammatical forms of language to express varying levels of respect and social hierarchy, falls precisely within the realm of tenor, serving as a clear example of how tenor manifests itself in language [53].
Japanese honorifics
In Japanese, honorifics are expressions, titles, grammatical forms, or phrases that directly embed the broader social context, formality, and hierarchy into the language. This embedding is so deep that mastery of honorifics proves mastery of the language and even the highest levels of social acumen. While it is possible to categorize honorifics into different groups by function, a complete taxonomy and elucidation of honorifics to such a degree is not necessary for this study (for detailed information, see [57]). The essential function here is that of the addressee honorifics, like です (desu) and ます (masu), which imply the social realities between interlocuters [58].
Grammar model overview
This section discusses the Japanese grammar model developed for this study and introduces pre-group grammar, atomic types and complex types, and particulars of the Japanese language.
Pre-group grammar: Atomic types and adjoints
Creating a quantum circuit in lambeq begins with defining the atomic types of a pre-group grammar. Atomic types combine into complex types. Grammatically intricate words receive complex types, while simpler words, like nouns, receive atomic types. The connectivity of the grammar is specified by pairing the atomic types with their left or right adjoints, which is so-called because types are abstractions of matrices. For example, s has a left-adjoint called s.l and a right-adjoint called s.r. The left and right nomenclature refers to the adjoint’s relative position to the noun. The right-adjoint, for example, will always be written to the right of the atomic type- i.e., n.r is always to the right of n. Adjoints can be chained, like s.l.l (the left-adjoint of the left-adjoint of s), which means that the s.l.l is to the left of an s.l that completes the pair. Figure 2 provides an example of these types and adjoints in a diagram. Lastly, the types combine using cups, as shown in Figure 3. The s wire is the only exception in a grammatically correct pre-group diagram.
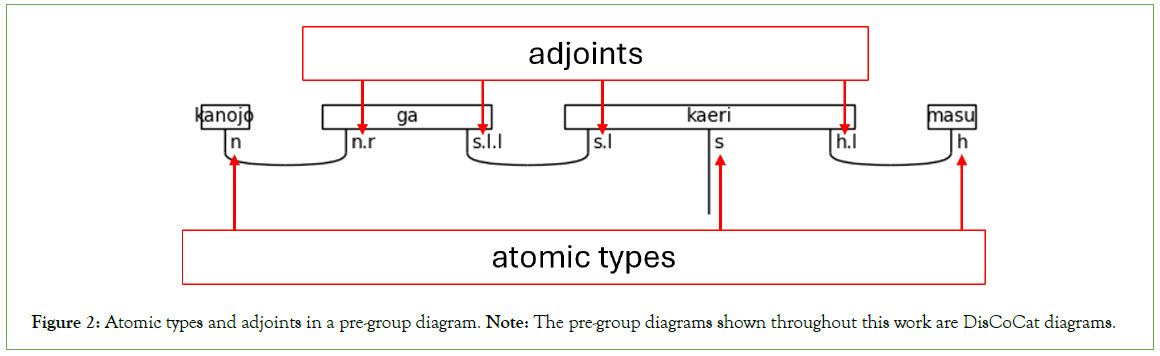
Figure 2: Atomic types and adjoints in a pre-group diagram. Note: The pre-group diagrams shown throughout this work are DisCoCat diagrams.
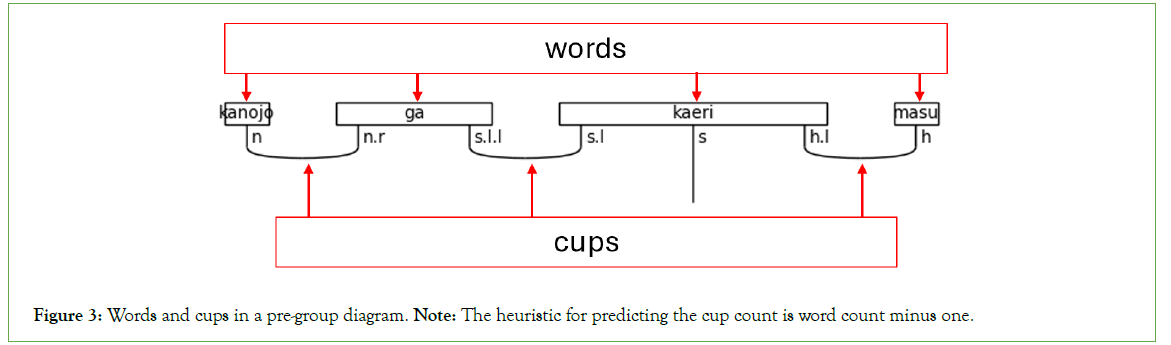
Figure 3: Words and cups in a pre-group diagram. Note: The heuristic for predicting the cup count is word count minus one.
Sentence-enders and meaning-carriers brief literature review
After defining atomic types, they are combined into complex types and assigned to words in a sentence. A Japanese sentence will always end with a verb, an い(i)-adjective, or the copula (述 語 (jyutsugo) is a general term that refers to any of these three parts of speech). Specifically, the final word always carries s in a casual, isolated sentence. When using the polite form, the final word always carries the interpersonal meaning via h, but it does not always contain s. Therefore, the final word does not always carry the textual meaning of the sentence. The grammar model must account for this when considering the predicate at large. In the following discussion, a sentence-ender is any grammatical type that can end a sentence. This term is a hypernym for verbs, the copula, and politeness markers. Whenever the sentence-ender does not carry the textual meaning of the sentence, the word that does so is the meaning-carrier. Again, this is a shorthand to identify the word that will include s in its complex type assignment. Note that the meaning-carrier is the adaptable word in the sentence. While it will always have an s, the number of particles, the presence of adverbs, other verbs, or even the presence of nouns will sometimes alter the meaning-carrier’s type assignment. Figure 4 is an example.
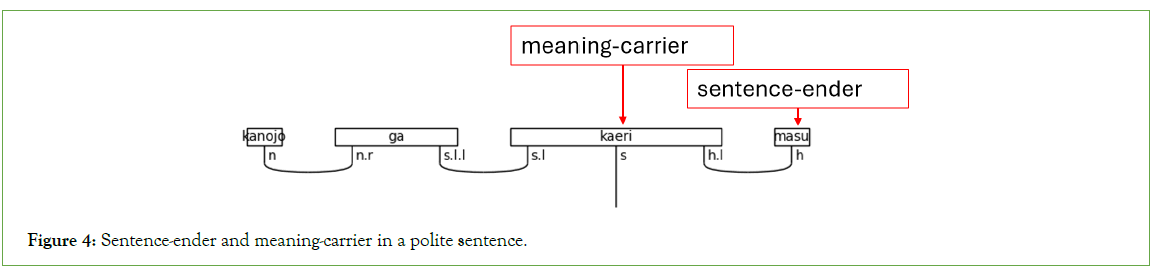
Figure 4: Sentence-ender and meaning-carrier in a polite sentence.
Complex types
This sub-section describes various parts of speech that the grammar model can process. These include particles, casual language, and polite language. Casual and polite language require different pre-group grammar diagrams to describe the behavior of verbs, adjectives, adverbs, the て (te) form verb, the copula, and verbal nouns.
Particles
In general, particles suffix nouns and specify the noun’s relationship to the verb’s action. Particles are words that explicitly define a sentence’s subject, object, and indirect object. They also, therefore, give Japanese flexibility regarding word order (Figure 5).
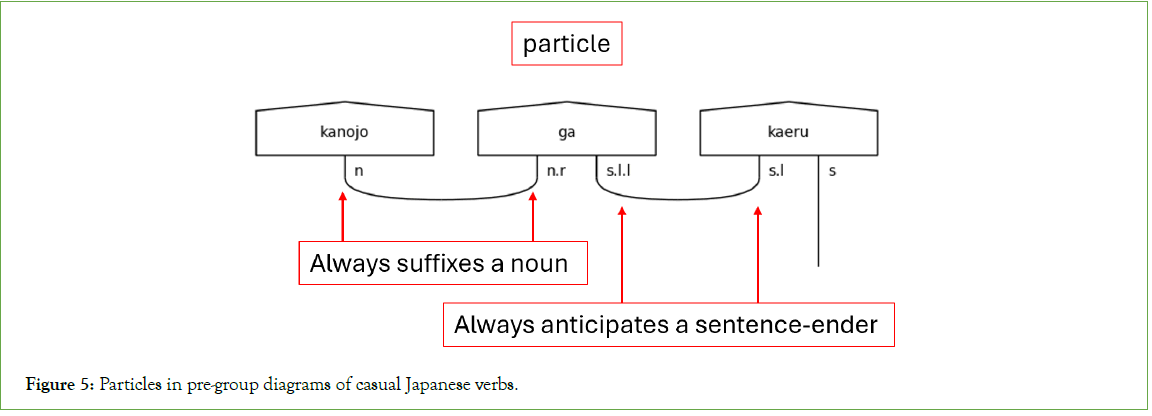
Figure 5: Particles in pre-group diagrams of casual Japanese verbs.
The exception in this model is the possessive, or genitive, particle の (no). の (no) will always link two nouns together, so it expects a noun on its left and right, like in Figure 6. The result is a composite noun that accepts particle suffixes as an independent noun in the sentence. This study excludes other uses of the particle の (no). Handling the different types of の (no) in this model is an avenue of future research (Figure 6).
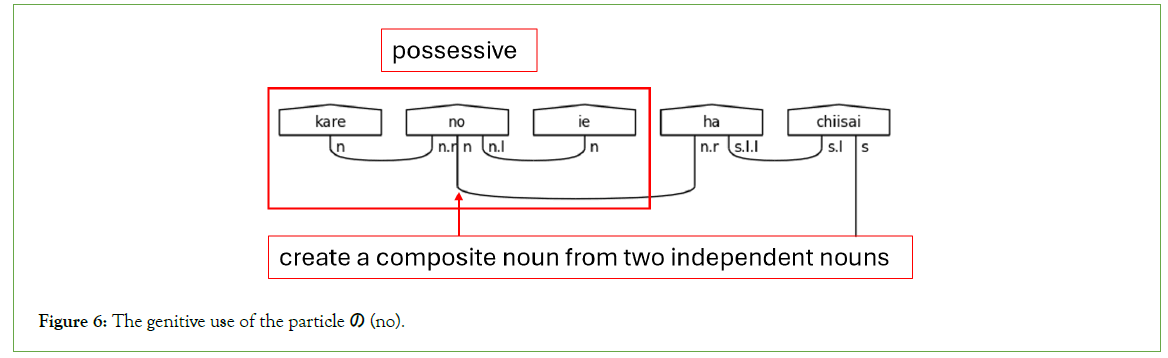
Figure 6: The genitive use of the particle の (no).
Casual language
Casual language has no honorifics, so its type assignments are the simplest. The foundational type is the casual verb because its assignment starts with a solitary s. The presence of particles will cause the type assignment of any sentence-ender to expand with one s.l type for each particle in the sentence, as shown in Figures 7 and 8. It is also worthy of note that the い (i)-adjective type is also s when it is the sentence-ender because い (i)-adjectives function as verbs when concluding sentences, as in Figure 8.
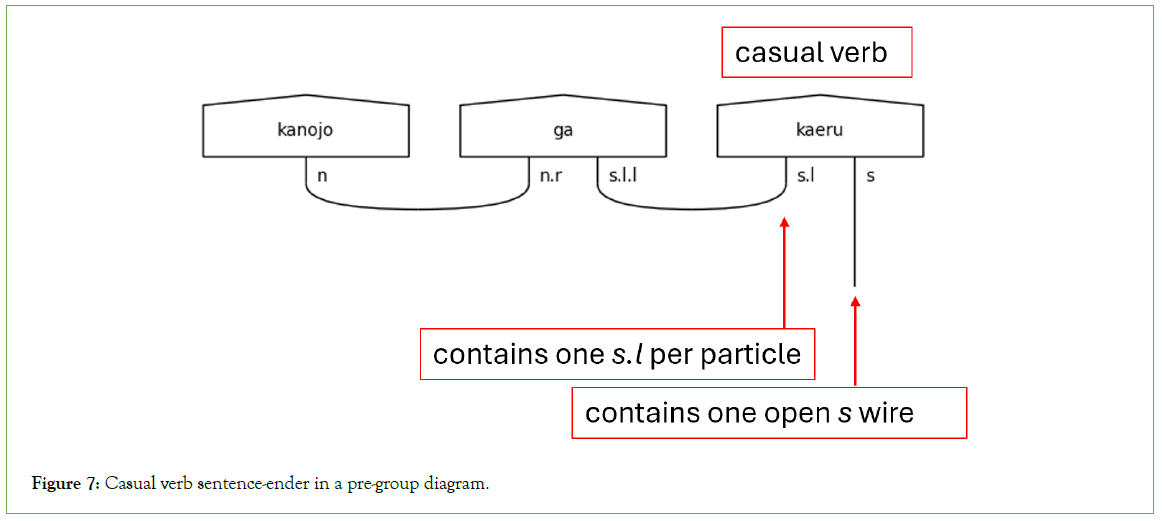
Figure 7: Casual verb sentence-ender in a pre-group diagram.
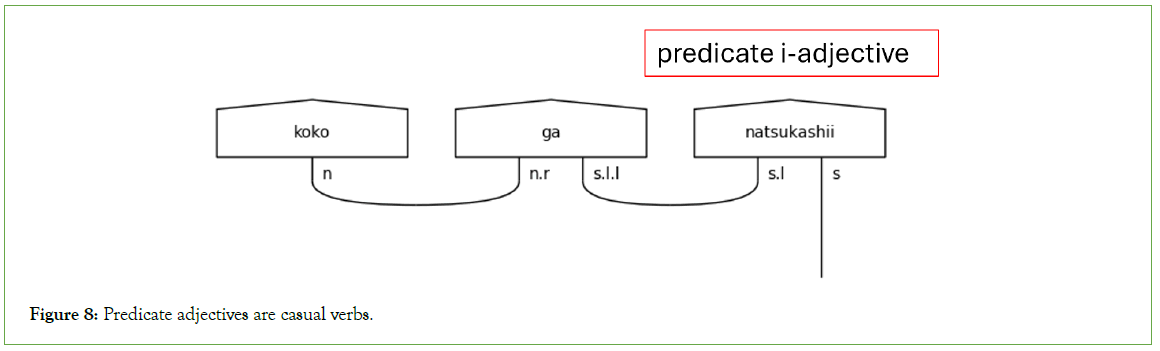
Figure 8: Predicate adjectives are casual verbs.
Japanese adverbs come primarily in two forms. The first is the な (na)-adjective, a noun suffixed with the に (ni) particle. This study parses these adjectives as nouns with a particle suffix. The second derives from い(i)-adjectives by changing the い(i) ending to く(ku), as in Figure 9. This derivation is a regular part of the language, so finding a “ku” in the predicate means finding an adverb.
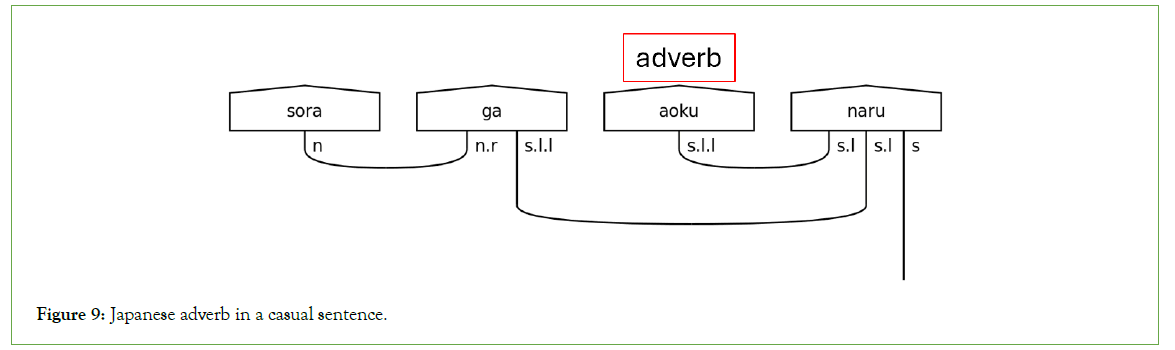
Figure 9: Japanese adverb in a casual sentence.
The て (te)-form is a particular form of a Japanese verb that modifies another subsequent verb. It, in effect, allows an entire verbal clause to modify another verb. When this occurs, the sentence’s particle links, the s.l types, join to the て (te)-form verb instead of the verb carrying the s type. Figure 10 demonstrates.
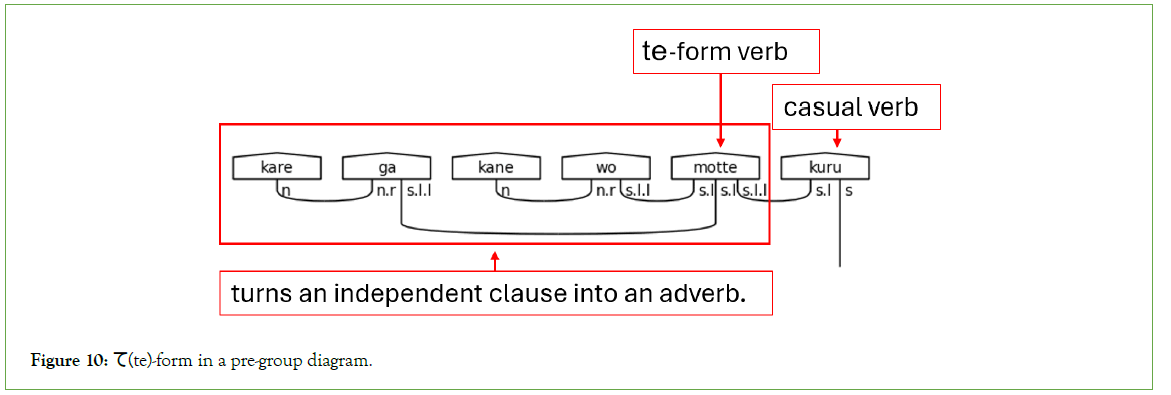
Figure 10: て(te)-form in a pre-group diagram.
Next, the copula だ (da) is unique in that it must suffix a noun like a particle, hence the n.r type on the left side of the copula’s complex type in Figure 11. Otherwise, だ (da) functions like a verb.
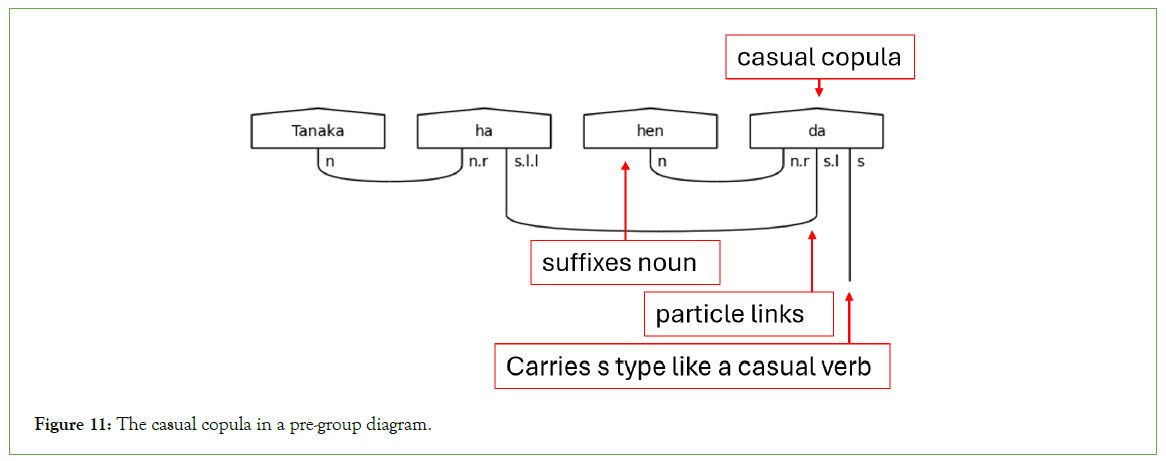
Figure 11: The casual copula in a pre-group diagram.
With casual sentences, there is a simple pattern. The connections flow from the left to the right. In the casual sentence-ender, noun terms, as in the case of だ (da), are defined on the leftmost side of the assignment. The particle links follow next, and the final term will always be the s term. This order always holds.
Polite language
With pre-groups, everything about casual language is also true for polite language, with two notable exceptions caused by including the h type. The first exception is the inclusion of h.l on the left side of s types in the polite-form verb. The second is the inclusion of the h type in the polite copula です (desu) on the left side of the n.r type. First, regarding the use of h.l, verbs in the polite form anticipate the helper verb ます (masu). ます (Masu) always has the type h. This rule is the archetypal example of a sentence-ender that is not a meaning- carrier. When ます (masu) is present, the polite form verb preceding the sentence-ender always carries the meaning. The same is also true of the predicate use of the adjective. There is no difference between the type assignments of polite verbs and predicate い (i)- adjectives paired with です (desu), as shown in Figures 12 and 13.
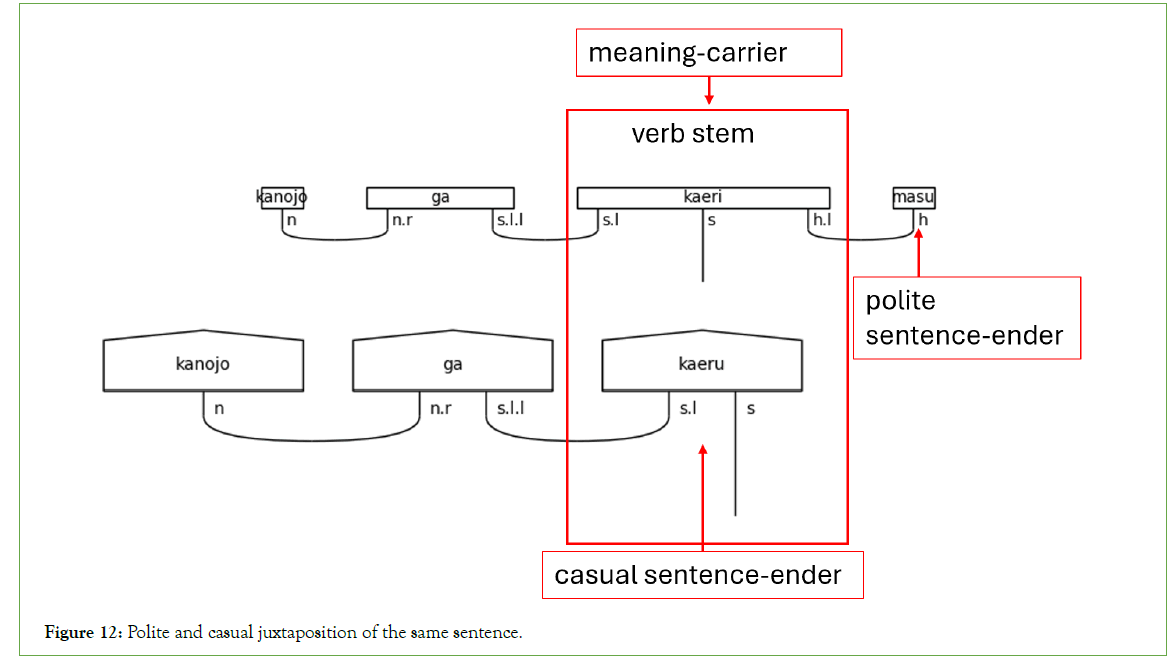
Figure 12: Polite and casual juxtaposition of the same sentence.
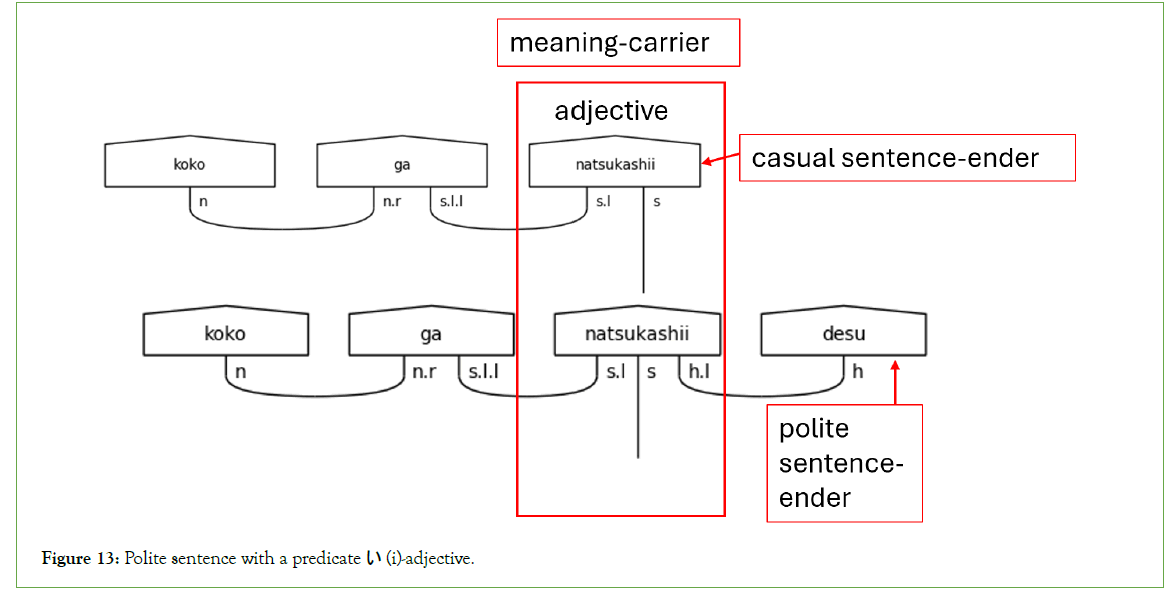
Figure 13: Polite sentence with a predicate い (i)-adjective.
Second, the h on the left side of n.r is a special case that occurs only withです (desu). This h causes the predicate noun preceding です (desu) to expect two cups. This expectation is because です (desu) serves two purposes in the sentence. Its first purpose is that of the copula the textual case of equivalence. The second purpose is to mark the sentence as polite the interpersonal case of honorifics. This dual purpose of a single word perfectly demonstrates the two- dimensional nature of Japanese sentences Figure 14 underscores this.
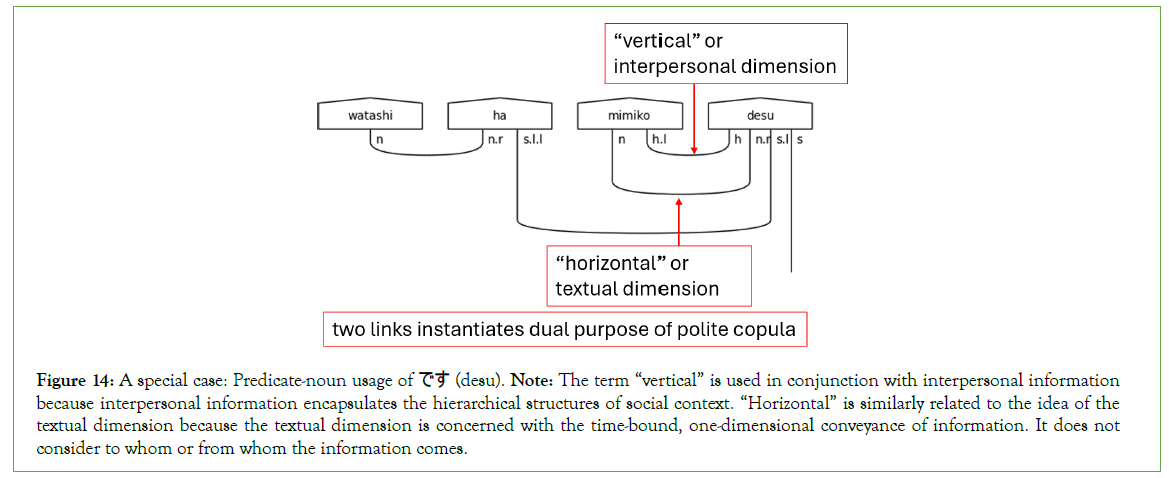
Figure 14: A special case: Predicate-noun usage of です (desu). Note: The term “vertical” is used in conjunction with interpersonal information because interpersonal information encapsulates the hierarchical structures of social context. “Horizontal” is similarly related to the idea of the textual dimension because the textual dimension is concerned with the time-bound, one-dimensional conveyance of information. It does not consider to whom or from whom the information comes.
A verbal noun is a noun with a verb suffixed directly onto it without having a particle as a buffer. In polite Japanese, the most common of these verbs is します (shi-masu), meaning “do” or “will do”. By suffixing します (shi-masu) to a noun, it simply means doing the noun’s action. Verbal nouns require an n.r type in the meaning- carrier since no particle is present to link the noun to the meaning- carrier し (shi). Figure 15 demonstrates a verbal noun’s behavior.
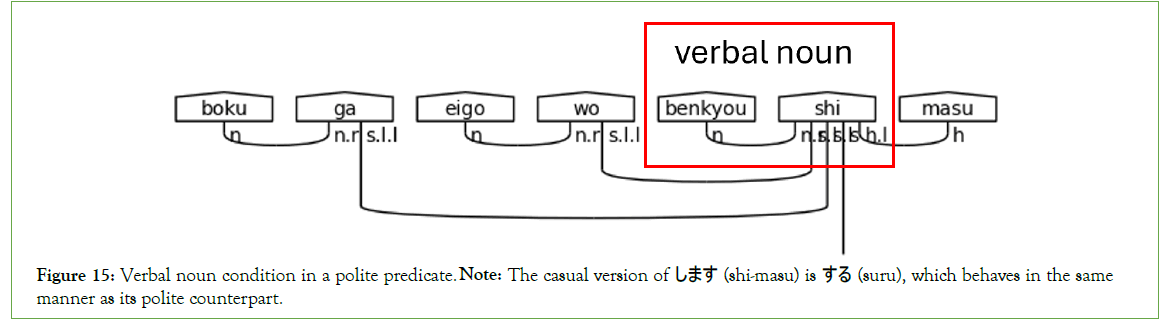
Figure 15: Verbal noun condition in a polite predicate. Note: The casual version of します (shi-masu) is する (suru), which behaves in the same manner as its polite counterpart.
Titles in Japanese are akin to those in English. The use of the most universally recognized title, さん (san), can be translated as “Mr.”, “Mrs.”, “Ms.”, “Miss” or any other related title. It specifies no sex or marital status. Instead, it simply elevates the use of a name in politeness. Since this is its function, it modifies the type of the name it suffixes. While it remains an n, a polite name also bears an h.l to anticipate the following title suffix, as in Figure 16.
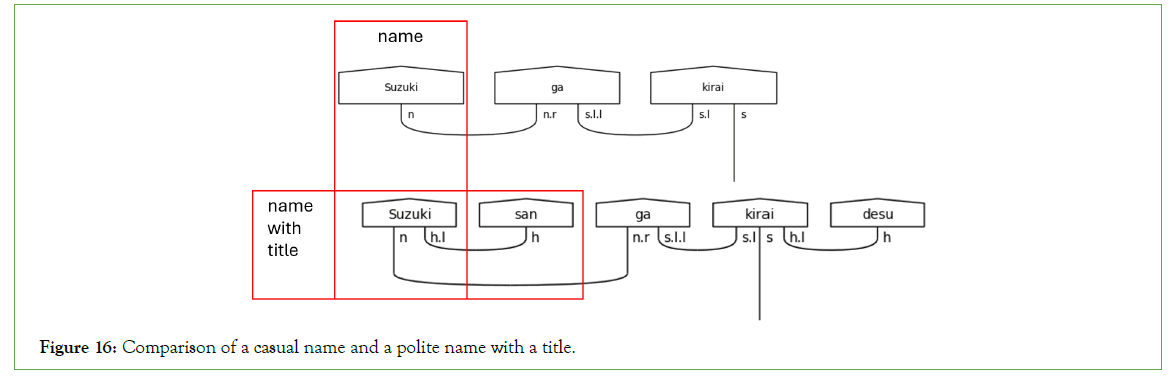
Figure 16: Comparison of a casual name and a polite name with a title.
Software implementation
This section discusses the limitations of software implementation using lambeq before introducing the diagramizer algorithm. The section continues with a discussion on functorially converting diagrams into quantum circuits. It then concludes with a discussion of the content and form of a quantum circuit that encodes the h type.
Limitations
Before discussing software implementation, limitations of contemporary Noisy Intermediate-Scale Quantum (NISQ) devices and the lambeq python package need to be acknowledged. First, deep circuits and complex language models those that feature many disparate atomic types are currently beyond their capabilities until fault tolerance, error correction, or other hardware advances occur [13].
That is a key reason why QNLP experiments have traditionally limited themselves to only the noun type, called n, or noun phrases, NP, and the sentence type, known as s [10,11]. This work pushes beyond that standard to include a third type: The honorific type h. However, incorporating more than three atomic types is beyond the scope of this experiment. This constraint also limits the present study to considering only two levels of honorifics, though the Japanese honorific system is significantly more complex than that. Further work can investigate additional atomic types and honorifics. Additionally, the availability of quantum hardware long queueing, limited vendors, and cost currently limits the design of this experiment.
Second, lambeq itself has some limitations. First, it cannot parse multiple sentences simultaneously. Though researchers are developing the capability to do so, it is not available to the open-source community at this time. The present study focuses on individual sentences rather than attempting to work around this limitation [59]. Further, lambeq has developed a parser, the BobcatParser, which only supports English. The depCCG parser, which does support Japanese, is not included in the lambeq installation, is not actively supported by lambeq, and is plagued by a bug in the depCCG installation process. The bug is a known issue but is not quickly resolved [60,61]. Because of this bug, parsing a non-English sentence into a pre-group diagram requires writing custom code using lambeq’s Application Programming Interface (API) [62]. This code resides on the author’s GitHub page [14].
The diagramizer algorithm
The purpose of the diagramizer algorithm is to parse a simple Japanese sentence into a pre-group diagram so that it can subsequently transform into a quantum circuit. The algorithm consists of eight steps:
1. Receive and validate the input.
2. Locate the indices of special words in the sentence.
3. Count the number of particles to prepare for assigning a complex type to the sentence-ender.
4. Assign the type to the predicate by identifying the sentence- ender and, if necessary, other special words found in the predicate.
5. Assign the type to the rest of the sentence.
6. Create a complete list of atomic types and adjoints.
7. Pair atomic types and adjoints with cups, marking the paired ones so the algorithm will not attempt to pair them again.
8. Draw the resulting diagram.
Step 1-Input validation: The algorithm proceeds as follows:
1. Confirm that the input sentence is not null.
2. Check if the sentence-ender is the copula だ (da).
a. If so, the sentence is valid.
3. Check if the sentence-ender’s final character is “u”.
a. If found, the sentence is valid.
4. Check if the sentence-ender’s final character is “I”.
a. If found, confirm the sentence-ender’s penultimate character is not “e”.
i. If not, the sentence ends in an い(i)-adjective and is valid.
5. If conditions 2, 3 or 4 are unmet, the sentence is invalid.
Input validation ensures essential grammatical rules are met rather than attempting to address every possible edge case. The sentence is valid if the casual copula だ (da) is present. Validation handles this case first because it is unusual. No other valid sentence-enders end with the “a” phoneme in this model. Even if a specific subject is not present, the sentence-ender in Japanese implies the subject so that it will produce a valid utterance even in isolation. The next check is looking for the ending phoneme “u”, which handles the case of です (desu), ます (masu), and non-past casual verbs. The “u” could be preceded by any of the consonantal sounds in Japanese and still yield a valid sentence-ender (i.e., う (u), く (ku), す (su), る (ru)). In this case, romaji makes the validation check easier since checking for “u” catches all valid word endings. The い (i)-adjective case requires a little more processing to ensure that the ending “i” character is not a common な (na)-adjective like 綺麗 (kirei) and 有名 (yuumei) by checking for “ei”. While this is not a perfect solution, as this also does not address common names, it is sufficient to handle every sentence encountered in this study’s corpus. In this case, kanji and kana characters would be more valuable as the い (i)-adjective must end with the hiragana い (i). There is no way to detect this perfectly without using kanji or treating “i” as a separate token. Investigating these approaches is left to future work. See Table 1 for examples of valid and invalid sentence-enders.
| Japanese | Transliteration | Part of Speech | Translation | Valid? |
|---|---|---|---|---|
| 嫌い | kirai | い(i)-adjective | “Dislike”, “hate” | Yes |
| 綺麗 | kirei | Noun or な(na)-adjective | “Beautiful”, “clean” | No |
| ます | masu | Verb | None | Yes |
| (Polite verb ender) | ||||
| 持つ | motsu | Verb | “Hold” | Yes |
| 源治 | Genji | Noun | None | No |
| (Name) | ||||
| だ | da | Copula | “is”, “am”, “are” | Yes |
| (Casual) | ||||
| です | desu | Copula | “is”, “am”, “are” | Yes |
| (Polite) | ||||
| Note: A な(na)-adjective is a noun that modifies another noun using the word な(na). It generally behaves as a noun and is, thus, considered as such here. An い(i)-adjective is a proper adjective in Japanese. The い(i)-adjective and な(na)-adjective monikers are ubiquitous in Japanese educational literature targeting native English speakers. | ||||
Table 1: Sentence-ender candidates and their validity.
Step 2-Index special words: The algorithm proceeds as follows:
1. Define a map where special words are keys and the values are empty lists.
2. For every word in the sentence:
a. If the word is one of the special words (keys) identified in Table 2.
| Japanese | Transliteration | Part of speech | Translation |
|---|---|---|---|
| は | ha | Particle | Topic marker |
| が | ga | Particle | Subject marker |
| に | ni | Particle | Dative marker |
| で | de | Particle | Locative or instrumental marker |
| を | wo | Particle | Accusative marker |
| の | no | Particle | “‘s” or “of” |
| (Genitive) | |||
| さん | san | Title | “Mr.”, “Ms.”, "Mrs." |
| だ | da | Copula | “is”, “am”, “are” |
| (Casual) | |||
| です | desu | Copula | “is”, “am”, “are” |
| (Polite) | |||
| ます | masu | Verb | None |
| (Polite verb ender) | |||
| Note: See cardinal’s master’s thesis for more information on the case markers in the translation column (2002). | |||
Table 2: Special words (keys) and their identification.
i. Append the index of the special word to the corresponding list.
b. If not, take no action.
A map of lists is flexible enough to handle multiple occurrences of the same special word occurring in different sentence positions. For example, it is common for the particle に (ni) to appear two or three times in the same sentence. The map collects the lists to make them accessible through a common data structure. Figure 17 illustrates the logic of step 2.
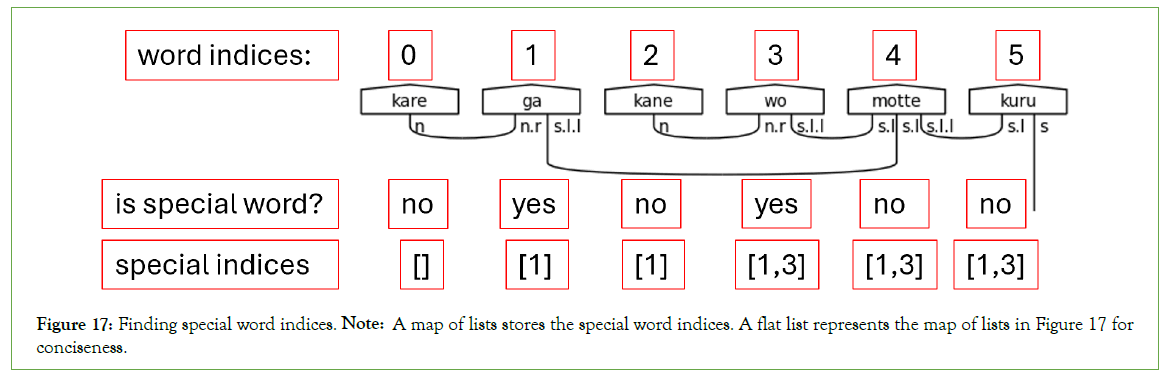
Figure 17: Finding special word indices. Note: A map of lists stores the special word indices. A flat list represents the map of lists in Figure 17 for conciseness.
Step 3- Count particles and build particle links: The algorithm is as follows:.
1. Define a particle count accumulator variable.
2. For each special word map key that represents a particle:
a. Determine the length of the value-the list of indices.
b. Add this length to the particle count accumulator.
3. Initialize a particle_links variable with the atomic type identity Ty.
4. For each counted particle, matrix multiply (@operator) the particle_links variable by s.l.
Because the number of particles can vary significantly, it is only possible to adequately type the predicate by first counting the number of particles in the sentence. Given the map of special words and lists of indices, particle counting proceeds as illustrated in Figure 18.
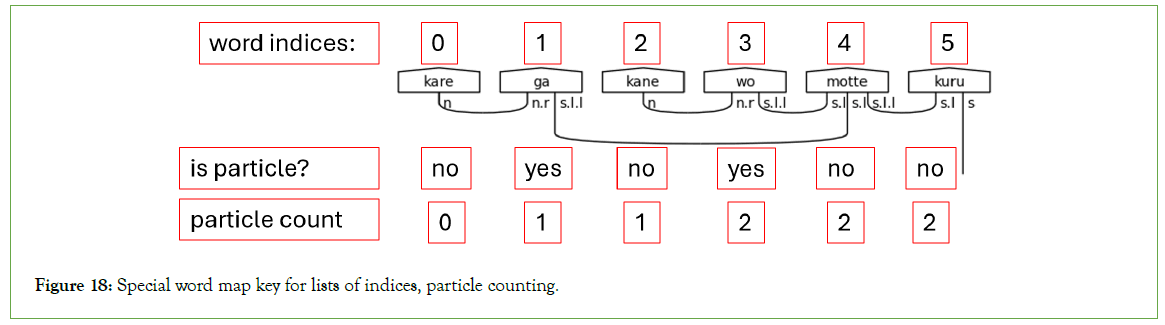
Figure 18: Special word map key for lists of indices, particle counting.
The particle count is then used to build a portion of the complex type needed for the predicate. This portion is called the particle links. The particle count is required because each particle must link to the predicate. The algorithm relies on the fact that an empty Ty the same lambeq class used to define the custom h type returns the atomic type identity value. Thus, by initializing the particle links variable with an empty Ty, the correct complex type can be constructed using iterative matrix multiplications as represented by the “@” operator. This approach allows for a programmatic construction of a particle link list of variable length, as shown in Figure 19.

Figure 19: Building particle links block visualization. Note: The “* n” represents the repetition of the “@ s.l” string in the figure n times.
Step 4-Assign the predictaes types: The algorithm proceeds as follows:
1. If the special word indices map keys だ (da) returns a non- empty list:
a. Assign sentence-ender type as n.r @ particle_links @ s.
2. If the special word indices map keys です (desu) returns a non- empty list:
a. If the word found at です (desu)’s index-1 ends with the final character “i” and its final two characters are not “ei”:
i. Assign the sentence-ender type as h.
ii. Assign the meaning-carrier type as
iii. particle_links @ s @ h.l. It is an い(i)-adjective.
b. Else, the word found at です(desu)’s index-1 is a noun.
i. Assign the sentence-ender type as
ii. h @ n.r @ particle_links @ s.
3. If the special word indices map keys ます (masu) returns a non- empty list:
a. Assign the sentence-ender type as h.
b. If the word found at ます (masu)’s index-3 ends with “ku”, then the predicate contains an adverb.
i. Assign the word found at ます (masu)’s index-3 as s.l.l.
ii. Assign the meaning-carrier as
iii. s.l @ particle_links @ s @ h.l.
c. If the word found at ます (masu)’s index-3 ends with “te”, then the predicate contains a て (te)-form verb.
i. Assign the word found at ます (masu)’s index-3 as
ii. particle_links @ s.l.l.
iii. Assign the meaning-carrier as s.l @ s @ h.l.
d. If the word found at ます (masu)’s index-2 is し (shi), and
the particle を (wo) is not found at ます (masu)’s index-3, then the predicate contains a verbal noun.
i. Assign the word found at ます (masu)’s index-3 as n.
ii. Assign the meaning-carrier as
iii. n.r @ particle_links @ s @ h.l.
e. Else, the word found at ます (masu)’s index-2 is a polite verb.
i. Assign the meaning-carrier as particle_links @ s @ h.l.
4. If the final word in the sentence ends with the character “i” and its final two characters are not “ei”, the word is an い(i)- adjective.
a. Assign the sentence-ender’s type as particle_links @ s.
5. If the final word in the sentence ends with the character “u”, then it is a casual verb.
a. If the penultimate word ends with “ku”, the predicate contains an adverb.
i. Assign the penultimate word as s.l.l.
ii. Assign the sentence-ender as s.l @ particle_links @ s.
b. If the penultimate word ends with “te”, then the predicate contains a て(te)-form verb.
i. Assign the penultimate word as particle_links @ s.l.l.
ii. Assign the sentence-ender as s.l @ s.
c. If the final word is する(suru), and the particle を(wo) is not the penultimate word, then the predicate contains a verbal noun.
i. Assign the penultimate word as n.
ii. Assign the sentence-ender as n.r @ particle_links @ s.
d. Else, the penultimate word does not alter the sentence- ender’s type assignment.
i. Assign the sentence-ender as particle_links @ s.
6. Else, the sentence is invalid.
Typing the predicate involves first determining which word is the sentence-ender. To that end, the algorithm checks the special word keys for だ (da), です (desu), and ます (masu) for a non-empty list. A special word does not end the sentence if all three return empty lists. The standard complex type for a casual verb or an い (i)-adjective is assigned instead. Note that casual sentences do not include a meaning-carrier as the sentence-ender carries the s type. If です(desu) is the sentence-ender, its type assignment will change depending on whether it succeeds an い(i)-adjective or a predicate noun. In the case of an い (i)-adjective, です (desu) functions purely honorifically. It carries only the h type.
The consequence is that the い (i)-adjective becomes the meaning- carrier in the sentence. In the case where the preceding word is a predicate noun, です (desu) will carry both the s type and the h type, requiring two cups between the predicate noun and です (desu), as shown in Figure 20. In this solitary case, it does not hold that the cup count equals word count minus one. This case is the archetypal example of how です(desu) functions simultaneously in the interpersonal (honorific) and textual sense.
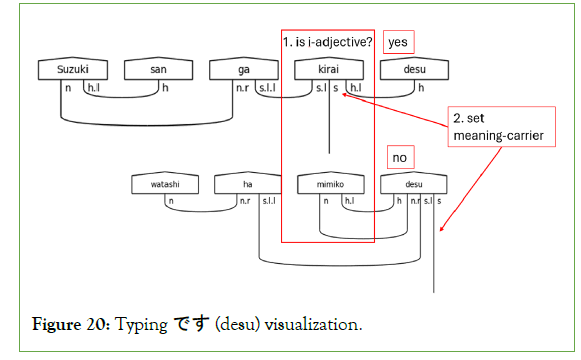
Figure 20: Typing です (desu) visualization.
If ます (masu) is the sentence-ender, then its type assignment is guaranteed to be h. The primary work of the algorithm is to determine the type assignment of the meaning-carrier, which will always be in the penultimate position of the sentence.
Adverbs may modify polite and casual verbs alike, て (te)-form verbs, or verbal nouns, which all alter the type of the meaning- carrier. Figure 21 visualizes this section of the algorithm from the perspective of polite verbs, but the logical flow applies equally to casual verbs.
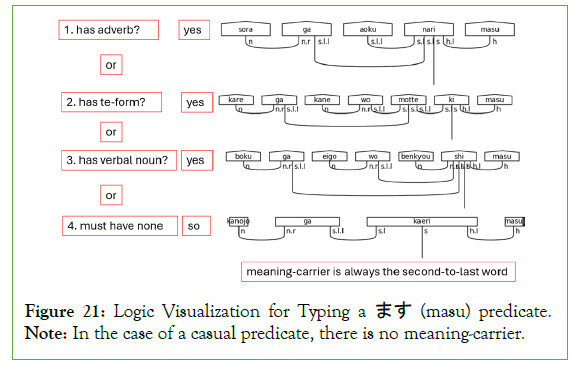
Figure 21: Logic Visualization for Typing a ます (masu) predicate. Note: In the case of a casual predicate, there is no meaning-carrier.
Step 5-Assign remaining types: The fifth step is consists of first assigning types to the indexed special words. It' then proceeds to assign types to the rest of the sentence using offsets from the indexed words as follows:
1. Assign the length of the word list to a variable called word_ count.
2. Initialize a new list, called types, of size word_count, containing the type assignments for the words in the sentence.
3. Assign the complex type of the sentence-ender to types[word_ count-1].
4. If there is a meaning-carrier:
a. Assign the complex type of the meaning-carrier to
b. types[word_count-2].
5. If the sentence-ender’s complex type is h @ n.r @ particle_links @ s:
a. If types[word_count-2] is unassigned:
i. Assign types[word_count-2] as n @ h.l.
6. If the sentence-ender’s complex type is n.r @ particle_links @ s:
a. If types[word_count-2] is unassigned:
i. Assign types[word_count-2] as n.
7. For each title that returns a list from the special word index map that is not empty:
a. Combine the lists into a new list and sort it.
b. For each instance of a title:
i. Assign types[title_index] as h.
c. If title_index ≥ 1 and types[title_index - 1] is unassigned:
i. Assign types[title_index-1] as n @ h.l.
8. If の (no) returns a list from the special word index map that is not empty:
a. For each instance of の (no):
i. Assign types[no_index] as n.r @ n @ n.l.
b. If no_index ≥ 1 and types[no_index-1] is unassigned:
i. Assign types[no_index-1] as n.
c. If no_index < word_count and types[no_index+1] is unassigned:
i. Assign types[no_index+1] as n.
9. For each particle that returns a list from the special word index map that is not empty:
a. Combine the lists into a new list and sort it.
b. For each instance of a particle:
i. Assign types[particle_index] as n.r @ s.l.l.
c. If particle_index ≥ 2 and types[particle_index-2] is unassigned:
i. Assign types[particle_index-2] as n @ n.l.
d. If particle_index ≥ 1 and types[particle_index-1] is unassigned:
i. Assign types[particle_index-1] as n.
10. Define a new list to hold lambeq words.
11. For each word in the word list and each type in the type list:
a. Instantiate a word by passing each word and its corresponding type by index into the word constructor.
b. Append the word to the list of words.
Note that the order of assignment of types in the algorithm is intentional. The assignment of types begins with the sentence- ender. The words directly linked to the sentence-ender the meaning- carrier, if present, or predicate nouns-are typed next. The rest of the predicate follows. The algorithm handles titles and names next, followed by the possessive particle の (no). The final portion handles the particles. This order allows for the appropriate assignment of types since the algorithm relies on indices and offsets.
Step 5 handles the predicate noun usage of です (desu), which requires drawing an additional cup, as in Figure 20. A typical pattern in the algorithm checks that offset words’ types are unassigned. This pattern prevents future type assignments from inadvertently overwriting previous ones. The index of the casual copula, だ (da), is used to type the noun it suffixes in the same manner as step 6.
Titles, の (no), and particles extend the offset checks to include list boundaries because their position in a sentence is not predetermined. Further, because the diagramizer algorithm assigns types from left to right, combined lists, like those for titles and particles, must be sorted into ascending order by index. Failure to do so results in particles with low index values failing to pair with nouns or verbs. Figure 22 illustrates the process.
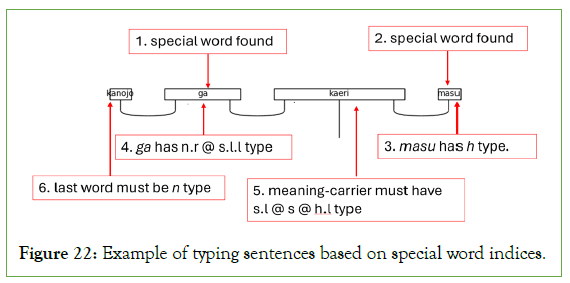
Figure 22: Example of typing sentences based on special word indices.
The algorithm handles particles last because they determine which words are adjectives. It is clear from the complex type of the particle that the preceding word is a noun. The less obvious trick is that any remaining unassigned types in the processing must be adjectives. Therefore, words receive adjective types by decrementing the particle index by two. The model, therefore, can account for adjectivally modified nouns suffixed with a logical particle. Figure 22 illustrates the algorithm up to step 9 and includes the order of operations. Figure 23 shows steps 10 and 11.
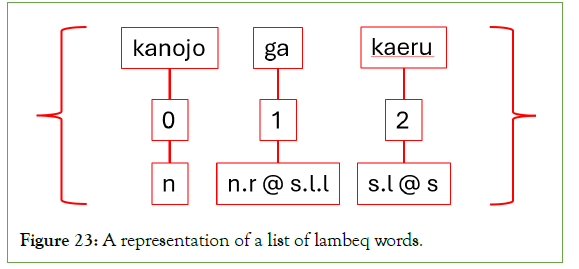
Figure 23: A representation of a list of lambeq words.
Step 6-Create the atomic type list: The algorithm proceeds as follows:
1. Initialize a string variable called atomic_types with “@” (at- sign).
2. For each type in the types list:
a. Cast the type into a string.
b. Concatenate the string onto atomic_types.
3. Split the atomic_types string into a list of sub-strings using “@” as the delimiter.
Based on the assigned types appended to the types list, a new list of atomic types must be created to facilitate the instantiation of lambeq cups. Cups expect atomic type indices, not word indices, as a part of their constructor. Figure 24 shows a graphical representation of the difference between atomic type indices and word indices.
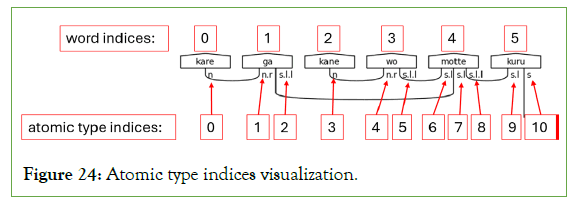
Figure 24: Atomic type indices visualization.
The at-sign is the delimiter because each list item with a complex type assignment includes this symbol as the separator for atomic types. The larger string will have a uniform separator between all atomic types by concatenating with this same symbol. The third and final step is to split the newly built string into a new list of atomic types and adjoints.
Step 7-Pair atomic types with adjoints using cups: The algorithm proceeds as follows:
1. Find the index of the s atomic type. Mark it as paired so that the algorithm ignores it. (The Boolean value true is an example).
2. Define a new list of cups.
3. Initialize a control variable named jump_distance as 1.
4. While the atomic_types list contains more than 1 unique value and the jump_distance is less than the length of the atomic_types list:
a. For each atomic type in the atomic_types list:
i. If atomic_types[i] is h.l and
ii. atomic_types[i+jump_distance] is h:
1. Instantiate a lambeq cup between the two types.
2. Append the cup to the cups list.
3. Mark the two types as paired.
iii. If atomic_types[i] is n.l and
iv. atomic_types[i+jump_distance] is n:
1. Instantiate a lambeq cup between the two types.
2. Append the cup to the cups list.
3. Mark the two types as paired.
v. If atomic_types[i] is h and
vi. atomic_types[i + jump_distance] is n.r :
1. Instantiate a lambeq cup between the two types.
2. Append the cup to the cups list.
3. Mark the two types as paired.
vii. If atomic_types[i] is s.l.l and
viii. atomic_types[i+jump_distance] is s.l:
1. Instantiate a lambeq cup between the two types.
2. Append the cup to the cups list.
3. Mark the two types as paired.
a. Increment jump_distance by 1.
Creating cups means connecting atomic types with their adjoints, simplifying them from the larger calculation. Only the s atomic type should remain unpaired, indicating a grammatically correct pre-group diagram. The processing concludes after marking all atomic types and adjoints as paired with a standard number, string, or Boolean. There are four potential match conditions for each item in the atomic_types list. Matches are either left-adjoints that pair with the atomic type (i.e., h.l to h), atomic types that pair with right-adjoints (i.e., n to n.r ), or double left-adjoints that pair with single left-adjoints (s.l.l to s.l). If one of these valid matches exists between the index and the index summed with the current jump distance, then a cup is instantiated. This process continues until no more un-matched candidates remain, running in worst case O(n2 ) time. Figure 25 illustrates the concept of jump distance the offset value used to find a potential match. Figure 26 illustrates the whole process.
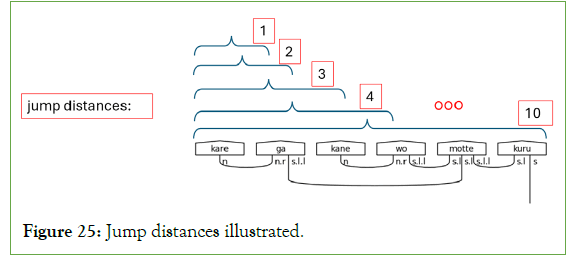
Figure 25: Jump distances illustrated.
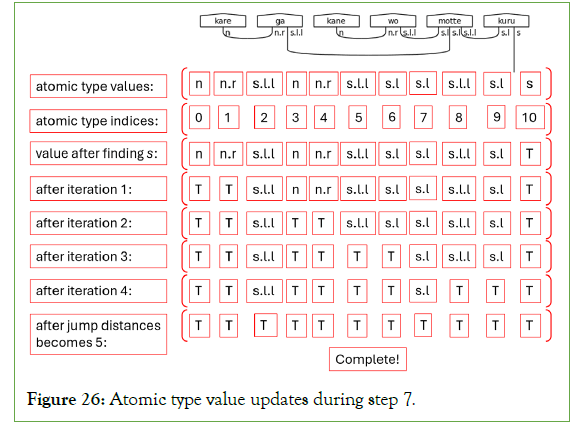
Figure 26: Atomic type value updates during step 7.
Step 8-Draw the pre-group diagram: After instantiating a word list and a cup list, all that remains is to draw the diagram. These two lists pass into the create_pre-group_diagram method of lambeq’s diagram static class. The lambeq library handles everything from there.
From diagram to circuit
Now that pre-group diagrams are constructed, the next step is to transform the pre-group diagrams into quantum circuits functorially. lambeq provides the core functionality. All that is needed is the pre-group diagram and an ansatz. Algorithmically, the process is the following:
• Instantiate a diagram variable using the diagramizer algorithm.
• Instantiate an ansatz.
• Simplify the diagram into its normal form.
• Simplify the diagram further by removing cups.
Ansatz refers to a parameterized quantum circuit used as the starting point of Quantum Machine Learning (QML) model training. Like the initial parameters fed into a neural network, the ansatz adjusts during training [63]. Normalizing a diagram means simplifying its wires into a standardized diagrammatic representation, like in Figure 22. Normalization removes spurious cups, caps, and wires via the snake equations [64,65]. After achieving this form, the remove cups rewriter removes the cups, further simplifying the diagram. Removing the cups reduces the post-selections in the quantum circuit, which yields significant performance improvements during QML experiment circuit evaluation [66,67]. The ansatz receives the simplified diagram, transforming it into a quantum circuit.
The transformation from diagrams to circuits is possible because of the underlying mathematical structures variations of monoidal categories that the two representations share. This transformation leverages a functor, a structure-preserving map in category theory that sends objects and morphisms of one category to another. In this study, the functor is the ansatz, and it sends the structure of the pre-group diagram (a rigid monoidal category) to the structure of the quantum circuit (a dagger-compact closed category) [68-73]. Simply put, functors allow one to translate common structures between different mathematical contexts. Figure 27 provides an example. They also, therefore, reveal common mathematical patterns in diverse disciplines.
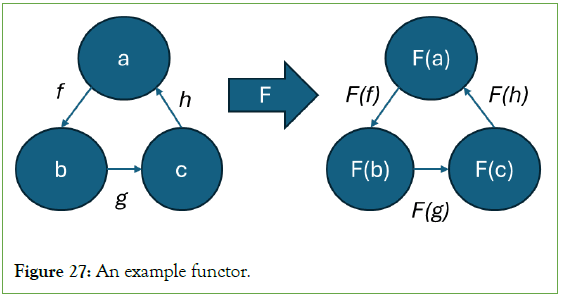
Figure 27: An example functor.
Reading quantum circuits for Japanese
It is now time to examine and discuss the structure of an example circuit that encodes honorific information. Figure 28 contains one such example.
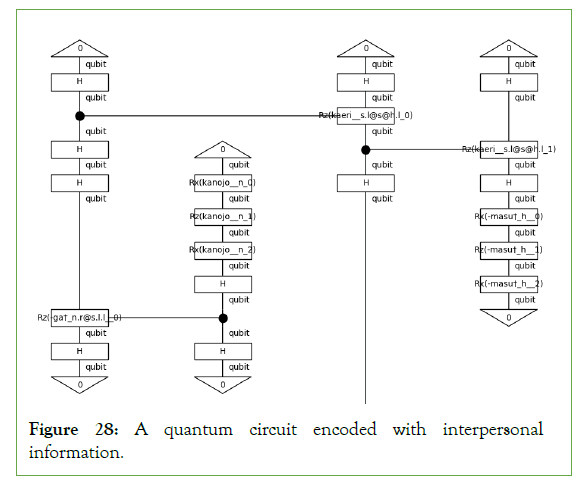
Figure 28: A quantum circuit encoded with interpersonal information.
The ansatz encodes the words in the quantum circuit. The ansatz used in this study is the Instantaneous Quantum Polynomial (IQP) ansatz, which creates layers from Hadamard gates and Controlled Rotation about the z-axis (CRz) gates to implement diagonal unitary matrices. For each word represented with a single qubit, three phase rotations are performed based on the n_single_qubit_params parameter. With an IQP ansatz, Euler decomposition represents the value of a qubit. This representation performs rotations about the x-axis, z-axis, and x-axis to set the qubit’s value.
Figure 28 is read from top to bottom as indicated by the open end of the 帰り (kaeri) wire; however, if one follows the sentence’s word order, the diagram has a spiral structure, as indicated by the outermost arrows in Figure 29. Assuming one is reading left to right, the first word of the sentence appears in the second position. The flow then follows the CRz gates that join the first and second positions together. The first position then controls the third, which controls the fourth. A solid black circle marks the control qubit. If this qubit’s value is |1>, then the Rz operation is performed on the target qubit by some angle θ, represented by the words inside the Rx and Rz gates [74-76].
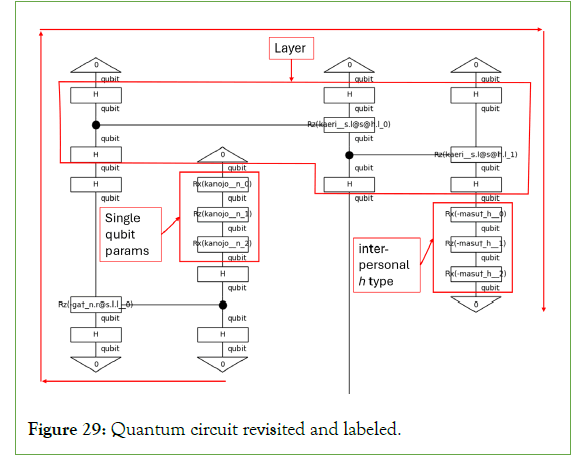
Figure 29: Quantum circuit revisited and labeled.
The fourth position in the diagram represents ます (masu). This position contains the h type of the sentence. This study, then, successfully demonstrated the encoding of a Japanese grammar model with explicit honorifics into a quantum circuit. In this implementation, the CRz gate controls the h type, which undergoes three phase rotations as the noun types do. Further work is needed to determine whether h warrants a specialized encoding. For now, it is enough to have demonstrated that encoding the interpersonal metafunction is possible.
A binary classification experiment
The experiment aims to show that trained parameterized circuits containing the h type can perform a binary classification task on labeled datasets. The datasets for this experiment include a training dataset with 100 sentences, a validation dataset with 80 sentences, and a test dataset with 80 sentences. Each sentence is labeled with a zero if it contains no honorifics or a one if at least one honorific type, h, is present. The circuit, therefore, will be learning to identify whether a sentence is polite or casual in Japanese. The experiment relies on the PennyLane model, which combines the classical and the quantum together into a promising new approach called quantum transfer learning [77,78]. PennyLane allows for simultaneous training of quantum circuits and neural networks and uses classical machine learning libraries, optimizers, and tools with quantum circuits [79].
Methods
The experiment requires the selection of several variables and their values. Table 3 shows these variables and the values selected for the experiment.
| Variable | Value |
|---|---|
| Batch size | 10 |
| Epochs | 15 |
| Learning rate | 0.1 |
| Seed | 42 |
| Optimizer | Adam W |
| Evaluation function | Accuracy |
| Loss | Mean-squared error |
| Ansatz | Types: n,s,h; |
| Qubits per type: 1 | |
| Layers: 2; | |
| Rotations: 3 | |
| Backend | Default. qubit |
| Rewriter | Unified codomain rewriter |
| Trainer | Pytorch trainer |
Table 3: Hyper-parameters and other key variables.
To prepare diagrams for the trainer, they were passed to a Unified Codomain Rewriter to pad them into a uniform tensor shape. The batch size refers to the number of diagrams the trainer processes simultaneously. The epochs are the number of complete passes to take over the training dataset. The learning rate refers to the magnitude of parameter adjustments during training. The trainer will use this value and the optimizer to calculate the gradient and perform gradient descent based on the result, which should improve the model’s performance on subsequent epochs. Next, the seed sets all the random number generators: one for PyTorch, one for the Python random number generator, and one for numpy. The selected optimizer is Adam W, a standard in academia.
The ansatz is the same as in Figure 28, except it uses two layers of Hadamard gates and unitary matrices. Lastly, as a note, this experiment was not run on real hardware due to limited availability and time, though individual circuits were sent to IBM hardware and evaluated to demonstrate that these circuits can run on real hardware (Appendix B for output). Training models on the rea hardware takes many hours or days due to queueing, so PennyLane’s default qubit backend configuration was deemed suitable for the full experiment. The selected evaluation function is accuracy, and the loss function is element-wise Mean Squared Error (MSE).
Results
Table 4 captures the results of the fifteen epochs. Figure 30, which follows, contains a graphical representation of the same data.
| Epoch | Training set loss | Validation set loss | Training set acc. | Validation set acc. |
|---|---|---|---|---|
| 1 | 0.3646 | 0.2893 | 0.475 | 0.55 |
| 2 | 0.2622 | 0.2516 | 0.7 | 0.6 |
| 3 | 0.251 | 0.2591 | 0.6 | 0.55 |
| 4 | 0.1559 | 0.2869 | 0.775 | 0.5125 |
| 5 | 0.1539 | 0.2719 | 0.8625 | 0.6 |
| 6 | 0.0726 | 0.2577 | 0.8875 | 0.5875 |
| 7 | 0.0616 | 0.2731 | 0.875 | 0.575 |
| 8 | 0.052 | 0.256 | 0.9375 | 0.575 |
| 9 | 0.0965 | 0.2755 | 0.9 | 0.575 |
| 10 | 0.0615 | 0.28 | 0.95 | 0.5625 |
| 11 | 0.05 | 0.3003 | 0.925 | 0.5125 |
| 12 | 0.0581 | 0.265 | 0.9125 | 0.6 |
| 13 | 0.0323 | 0.2503 | 0.9375 | 0.5625 |
| 14 | 0.0565 | 0.239 | 0.9375 | 0.6375 |
| 15 | 0.0153 | 0.2631 | 0.9625 | 0.6125 |
| Note: Columns four and five report the accuracy as decimal values. Multiplying them by 100 yields percentages | ||||
Table 4: Results of model fitting to training set and validation set.
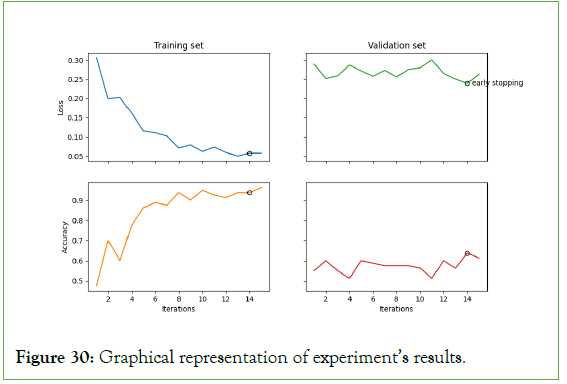
Figure 30: Graphical representation of experiment’s results.
The training set results in columns two and four exhibit strong positive trends. The loss decreases to under 2%, while the accuracy steadily increases to over 96%. This behavior is ideal and expected for the training set. However, these results can be deceptive, so models must always be checked against a validation set for a more accurate measure of performance. Columns three and five contain the results of the fifteen epochs against the validation set. The trend here could be more positive. In fifteen epochs, the validation set’s loss does not improve. It continues to hover between 20% and 30%. The accuracy also vacillates, eventually exceeding 61%. This result reveals that the model is learning its training data very well; however, it also reveals a limitation. It is learning the training set too well and overfitting.
The test set is reserved for after the training is completed and is used to gauge the performance of the model’s first prediction. Since the model has never seen the data in the test set, it is a good test of its performance in a production environment. Upon performing its first prediction on the test set, the model’s accuracy is 70%, confirming that it is not ready for production. That said, 96%, 61%, and 70% scores are better than guessing. Since the purpose of this experiment was to prove that interpersonal data from the Japanese language can be encoded into quantum circuits and used for QML, it is deemed a success. Future work can further this preliminary result with a production quality experiment (Table 5).
| Training result | Validation result | Test result |
|---|---|---|
| 96.25% | 61.25% | 70.00% |
Table 5: Collected results on training, validation, and test subsets as percentages.
Discussion
Summary of contributions
This work contributes the following to the body of QNLP research:
1. Leverages lambeq’s custom type functionality to encode the interpersonal metafunction of SFL by defining the custom type h. A binary classification experiment used circuits encoding the h type. Though overfitting limits the usefulness of the experiment presented in this paper, the experiment is still a preliminary demonstration of the potential value of circuits embedded with the h type.
2. Provides a Japanese grammar model, utilities, and a novel algorithm for parsing Japanese sentences using lambeq. The source code is available on GitHub for other researchers.
3. Encourages exploration into different language models, like SFL, and exploration into non-textual information in further experiments.
4. Introduces the concept of multi-dimensionality in the Japanese language where vertical meaning refers to interpersonal information SFL’s interpersonal metafunction encoded in grammar and horizontal meaning refers to textual information SFL’s textual metafunction.
Summary of avenues for further research
This work recommends the following avenues of future research based on its contributions:
1. Extending lambeq with a standardized h type and the ability to parse Japanese sentences natively.
2. Exploring complex Japanese types that account for the subtle, yet crucial, differences between particles nominative, accusative, ablative, and genitive cases.
3. Modifying source code to improve input validation, the diagramizer algorithm, and to make the grammar model more robust.
4. Considering other languages and linguistic realities, the research community is missing by focusing too much on English and neglecting low-resource languages.
5. Applying more mathematical rigor to the concept of multi- dimensional meaning, extending it to account for all metafunctions of SFL, and presenting it as a conceptual space.
6. Currently, the h type is represented in quantum circuits using the same Euler decomposition as a noun, so it is left to future work to investigate whether h should receive a unique encoding.
7. Create a version of the diagramizer algorithm that processes kanji and kana.
Conclusion
This preliminary study has shown that encoding the interpersonal meaning of language into a quantum circuit is possible and could yield fruitful results in future QML experiments and quantum applications. Additionally, this endeavor encourages the research community to explore new linguistic avenues of research. Language encompasses the full spectrum of human experience. For research to be complete and fair, it must pay attention to every language function and consider the nuances of low-resource languages. QNLP’s ability to encode the grammar directly into the model perfectly leverages quantum hardware’s capability to compute vector spaces. Ultimately, QNLP is a potential path forward toward consistent, verifiable natural language processing that cannot be ignored.
Author contributions
Ryder Dale Walton contributed all the original work to this article.
Funding
This research received no external funding.
Data availability statement
The source code is available on GitHub (Walton, 2024).
Acknowledgments
Special thanks to my wife, Lindsay, our beautiful children, our extended family, and all our friends and co-workers for all their support and prayers. Also, I thank Dimitri Kartsaklis for providing a working code sample of the Unify Codomain Rewriter. Without his help, the experiment would have taken considerably more troubleshooting time. Lastly, thanks to Matthieu Pageau for the inspiration to integrate computer science with theology, philosophy, and metaphysics.
Conflicts of interest
The author declares no conflicts of interest.
References
- Matthiessen CM, Halliday MA. Systemic functional grammar: A first step into the theory. 1997.
- Sekizawa R, Yanaka H. Analyzing syntactic generalization capacity of pre-trained language models on Japanese honorific conversion. arXiv preprint arXiv:2306.03055. 2023.
- Hall ET. Beyond culture. Anchor. 1976.
- Kartsaklis D, Fan I, Yeung R, Pearson A, Lorenz R, Toumi A, et al. lambeq: An efficient high-level python library for quantum NLP. arXiv preprint arXiv:2110.04236. 2021.
- Quantinuum. lambeq: An efficient high-level Python library for quantum NLP. GitHub. 2024.
- Coecke B, de Felice G, Meichanetzidis K, Toumi A. Foundations for near-term quantum natural language processing. arXiv preprint arXiv:2012.03755. 2020.
- Wang-Mascianica V, Liu J, Coecke B. Distilling text into circuits. arXiv preprint arXiv:2301.10595. 2023.
- Coecke B, Felice GD, Meichanetzidis K, Toumi A. How to make qubits speak. 2021.
[Crossref]
- Metawei MA, Taher M, ElDeeb H, Nassar SM. A topic-aware classifier based on a hybrid quantum-classical model. Neural Comput Appl. 2023;35(25):18803-18812.
- Meichanetzidis K, Toumi A, de Felice G, Coecke B. Grammar-aware sentence classification on quantum computers. Quantum Mach Intell. 2023;5(1):10.
- Yeung R, Kartsaklis D. A CCG-based version of the DisCoCat framework. arXiv preprint arXiv:2105.07720. 2021 May 17.
- Zeng W, Coecke B. Quantum algorithms for compositional natural language processing. arXiv preprint arXiv:1608.01406. 2016.
- Walton RD. Self-move and other-move: Quantum categorical foundations of Japanese. arXiv preprint arXiv:2210.04451. 2023.
- Walton RD. Verticle_meaning. GitHub. 2024.
- Wang-Mascianica V, Coecke B. Talking Space: Inference from spatial linguistic meanings. arXiv preprint arXiv:2109.06554. 2021.
- Guarasci R, De Pietro G, Esposito M. Quantum natural language processing: Challenges and opportunities. Appl Sci. 2022;12(11):5651.
- Wu A, Li G, Wang Y, Feng B, Ding Y, Xie Y. Towards efficient ansatz architecture for variational quantum algorithms. arXiv preprint arXiv:2111.13730. 2021.
- Coecke B. Quantum pictorialism. Contem Phys. 2010:59-83.
[Crossref]
- Coecke B. From quantum foundations via natural language meaning to a theory of everything. The Incomputable: Journeys Beyond the Turing Barrier. 2017:63-80.
- Coecke B. The mathematics of text structure. Joachim Lambek: The Interplay of Mathematics, Logic, and Linguistics. 2021:181-217.
- Coecke B, Gogioso S. Quantum in Pictures. 2022.
- Coecke B, Lewis M, Marsden D. Internal wiring of Cartesian verbs and prepositions. arXiv preprint arXiv:1811.05770. 2018.
- Liu J. Jonathan Liu – DisCoCirc. 2023.
- Rizzo I. A tale of deals, no deals, and baked beans. 2019.
- Waseem MH, Liu J, Wang-Maścianica V, Coecke B. Language-independence of DisCoCirc's text circuits: English and Urdu. arXiv preprint arXiv:2208.10281. 2022.
- van de Wetering J. ZX-calculus for the working quantum computer scientist. arXiv preprint arXiv:2012.13966. 2020.
- Lambek J. Type grammar revisited. Springer Berlin Heidelberg. 1997:1-27.
- Cardinal K. An algebraic study of Japanese grammar. 2002.
- Cardinal K. A pre-group analysis of Japanese causatives. Korean Soc Lang Info. 2007:96-104.
- de Felice G. Categorical tools for natural language processing. arXiv preprint arXiv:2212.06636. 2022.
- Coecke B, Paquette EO. Categories for the practising physicist. arXiv:0905.3010. 2009.
- Toumi A. Category theory for quantum natural language processing. arXiv preprint arXiv:2212.06615. 2022.
- Coecke B, Wang V. Grammar equations. 2021.
[Crossref]
- Coecke B, de Felice G, Marsdenm D, Toumi A. Towards compositional distribution discourse analysis. Electron Proc Theor Comput Sci. 2018:1–12.
[Crossref]
- Coecke B, Kissinger A. Picturing quantum processes: A first course on quantum theory and diagrammatic reasoning. Cambridge: Cambridge University Press, Springer International Publishing. 2018:28-31.
- Coecke B, Sadrzadeh M, Clark S. Mathematical foundations for a compositional distributional model of meaning. arXiv preprint arXiv:1003.4394. 2010.
- Feynman RP. Simulating physics with computers. In Feynman and computation. CRC Press. 2018:133-153.
- Kartsaklis D. Compositional distributional semantics with compact closed categories and frobenius algebras. arXiv preprint arXiv:1505.00138. 2015.
- Rodatz B, Shaikh RA, Yeh L. Conversational negation using worldly context in compositional distributional semantics. arXiv preprint arXiv:2105.05748. 2021.
- Shaikh RA, Yeh L, Rodatz B, Coecke B. Composing conversational negation. arXiv preprint arXiv:2107.06820. 2021.
- Lewis M. Modelling hyponymy for DisCo-Cat. InProceedings of the Applied Category Theory Conference, Oxford, UK 2019.
- Lewis M. Towards logical negation for compositional distributional semantics. arXiv preprint arXiv:2005.04929. 2020.
- Duneau T. Parsing conjunctions in DisCoCirc. In Proceedings of the 2021 Workshop on Semantic Spaces at the Intersection of NLP, Physics, and Cognitive Science (SemSpace). 2021:66-75).
- Lorenz R, Pearson A, Meichanetzidis K, Kartsaklis D, Coecke B. QNLP in practice: Running compositional models of meaning on a quantum computer. J Artif Intell Res. 2023;76:1305-1342.
- Abbaszade M, Salari V, Mousavi SS, Zomorodi M, Zhou X. Application of quantum natural language processing for language translation. IEEE Access. 2021;9:130434-130448.
- Abbaszade M, Zomorodi M, Salari V, Kurian P. Toward quantum machine translation of syntactically distinct languages. arXiv preprint arXiv:2307.16576. 2023.
- Vicente Nieto I. Towards machine translation with quantum computers. 2021.
- Peral-García D, Cruz-Benito J, García-Peñalvo FJ. Systematic literature review: Quantum machine learning and its applications. Comput Sci Rev. 2024;51:100619.
- Putz V, Svozil K. Quantum music. arXiv:1503.09045. 2015.
[Crossref]
- Xue C, Chen ZY, Zhuang XN, Wang YJ, Sun TP, Wang JC, et al. End-to-end quantum vision transformer: Towards practical quantum speedup in large-scale models. arXiv preprint arXiv:2402.18940. 2024.
- Liu J. Language as circuits (Doctoral dissertation, MSc Thesis, University of Oxford). 2021.
- Liu J, Shaikh RA, Rodatz B, Yeung R, Coecke B. A pipeline for discourse circuits from CCG. arXiv preprint arXiv:2311.17892. 2023.
- Liu M, Kobayashi I. Construction and validation of a Japanese honorific corpus based on systemic functional linguistics. In Proceedings of the Workshop on Dataset Creation for Lower-Resourced Languages within the 13th Language Resources and Evaluation Conference 2022:19-26.
- Thompson G, Bowcher WL, Fontaine L, Schönthal D, editors. The Cambridge handbook of systemic functional linguistics. Cambridge: Cambridge University Press; 2019.
- Cerban M. The interpersonal metafunction of clauses: Polarity and modality. In Proceedings of the International Conference Challenges in Language, Literature and Arts at the Beginning of the 21st Century”, Germanic Languages.2009
- Leung A. Field, tenor, and mode-a literacy framework for all subjects. 2016.
- Potts C, Kawahara S. Japanese honorifics as emotive definite descriptions. In Semantics and linguistic theory. 2004:253-270.
- Yamada A. The syntax, semantics and pragmatics of Japanese addressee-honorific markers. Georgetown University. 2019.
- Chang DT. Variational quantum classifiers for natural-language text. arXiv preprint arXiv:2303.02469. 2023.
- Quantinuum. depccg support: In lambeq installation. 2024.
- Yoshikawa M. Issue #37: Error while installing. depccg [Issue]. GitHub. 2023.
- de Felice G, Toumi A, Coecke B. DisCoPy: Monoidal categories in python. arXiv preprint arXiv:2005.02975. 2020.
- Wu S, Li J, Zhang P, Zhang Y. Natural language processing meets quantum physics: A survey and categorization. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing 2021:3172-3182.
- Coecke B. Compositionality as we see it, everywhere around us. InThe Quantum-Like Revolution: A Festschrift for Andrei Khrennikov. Cham: Springer International Publishing. 2023:247-267.
- Quantinuum. Rewriting: In lambeq documentation. 2024.
- Quantinuum. Training: Hybrid case, in lambeq documentation. 2024.
- Aaronson S. Quantum computing, postselection, and probabilistic polynomial-time. Proc R Soc A: Math Phys Eng Sci. 2005;461(2063):3473-3482.
- Crooks GE. Quantum Gates. 2024.
- Howard J, Gugger S. Deep learning for coders with Fastai and PyTorch. O'Reilly Media. 2020.
- Loshchilov I, Hutter F. Decoupled weight decay regularization. arXiv preprint arXiv:1711.05101. 2017.
- Matthiessen CM, Halliday MA. Systemic functional grammar: A first step into the theory. 1997.
- Meichanetzidis K, Gogioso S, De Felice G, Chiappori N, Toumi A, Coecke B. Quantum natural language processing on near-term quantum computers. arXiv preprint arXiv:2005.04147. 2020.
- Pizziconi B. Honorifics: The cultural specificity of a universal mechanism in Japanese. Politeness in East Asia. 2011:45-70.
- Quantinuum. BobcatParser, lambeq. 2024.
- Takekuro M. Attunement in interaction: Sequential use of Japanese honorifics. University of California, Berkeley. 2005.
- Yoshikawa M. depccg: A combinatory categorial grammar parser. GitHub. 2023
- O’Riordan LJ, Doyle M, Baruffa F, Kannan V. A hybrid classical-quantum workflow for natural language processing. Mach Learn.: Sci. Technol. 2020;2(1):015011.
- Buonaiuto G, Guarasci R, Minutolo A, De Pietro G, Esposito M. Quantum transfer learning for acceptability judgements. Quantum Mach Intell. 2024;6(1):13.
- Xanadu. Penny lane. 2024.
Citation: Walton RD (2024) Vertical Meaning: Introducing and Exercising Interpersonal Data in Quantum Circuits ,via Japanese Honorifics. Int J Swarm Evol Comput. 13:379.
Copyright: © 2024 Walton RD. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.