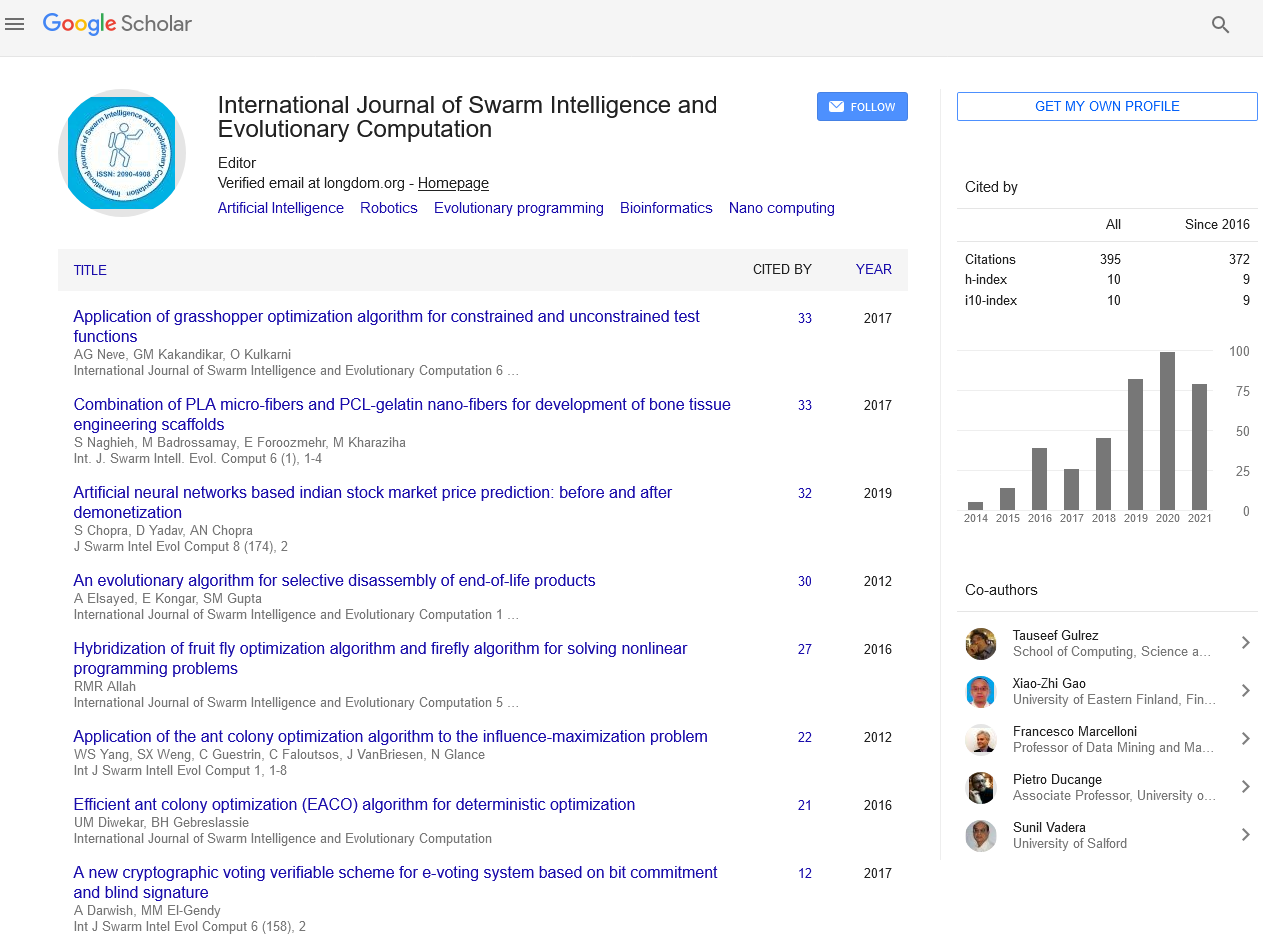
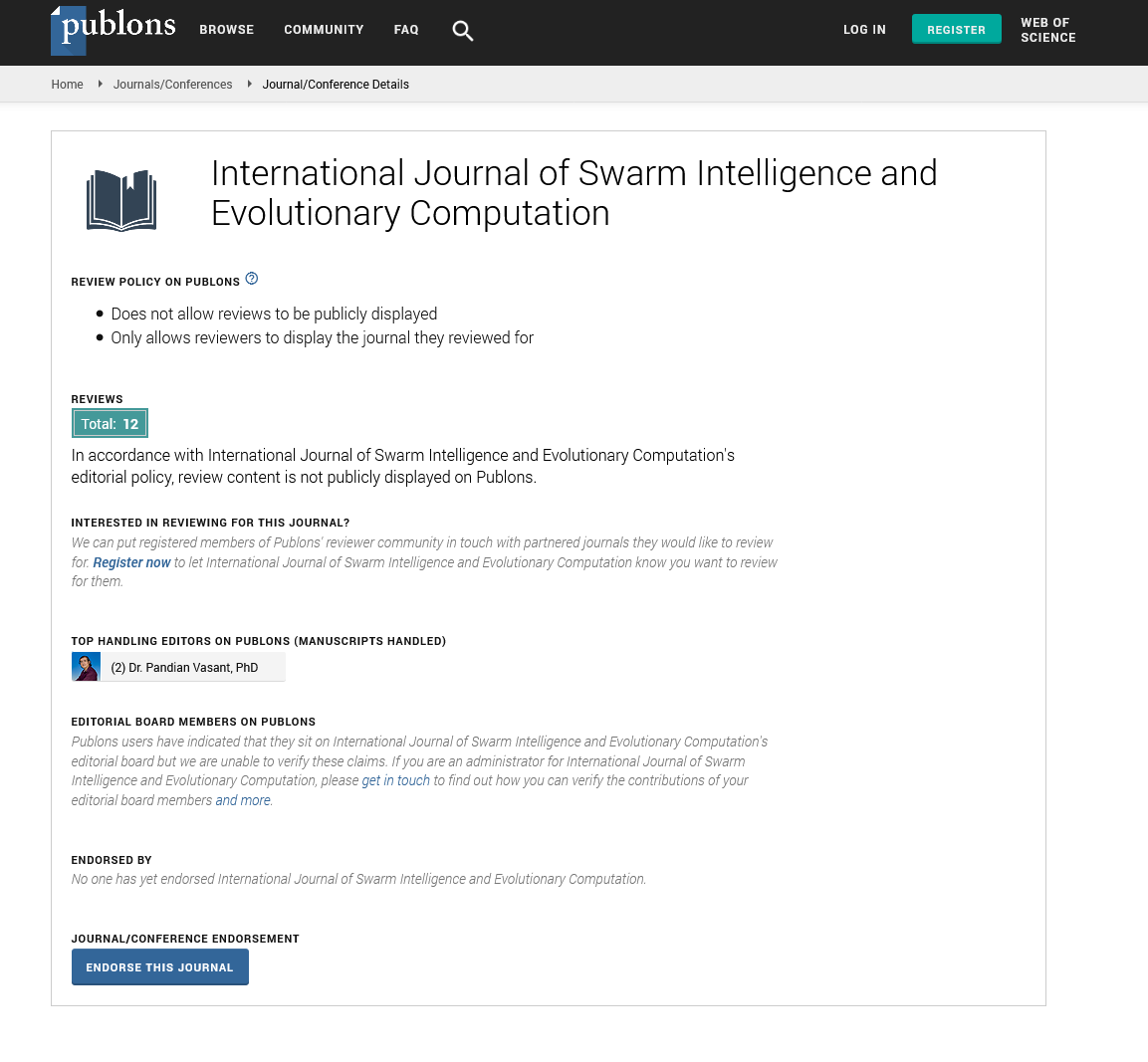
Indexed In
- Genamics JournalSeek
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Publons
- Euro Pub
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Perspective - (2024) Volume 13, Issue 3
Towards Intelligent Decision-Making: Advancing Probabilistic Computing for Real-World Applications
Darcy Williams*Received: 26-Apr-2024, Manuscript No. SIEC-24-25857; Editor assigned: 29-Apr-2024, Pre QC No. SIEC-24-25857 (PQ); Reviewed: 14-May-2024, QC No. SIEC-24-25857; Revised: 21-May-2024, Manuscript No. SIEC-24-25857 (R); Published: 29-May-2024, DOI: 10.35248/2090-4908.24.13.373
Description
Probabilistic computing represents a change of opinion in computational thinking, where uncertainty is not only acknowledged but embraced as a fundamental aspect of decisionmaking. Rooted in probability theory, probabilistic computing offers powerful techniques for modeling uncertainty, reasoning under uncertainty, and making informed decisions in complex and uncertain environments.
Principles of probabilistic computing
At its core, probabilistic computing is founded on the principles of probability theory and Bayesian inference. The key principles include:
Probability distributions: Probabilistic computing models uncertainty using probability distributions, which quantify the likelihood of different outcomes or states of the world.
Bayesian inference: Bayesian inference provides a principled framework for updating beliefs and making decisions in light of new evidence. It enables the incorporation of prior knowledge and uncertainty into the decision-making process.
Probabilistic programming: Probabilistic programming languages allow the specification of probabilistic models using high-level programming constructs. These languages enable the development of complex probabilistic models and facilitate inference and analysis.
Monte carlo methods: Monte Carlo methods, such as Markov Chain Monte Carlo (MCMC) and Variational Inference (VI), are used for approximate inference in probabilistic models. These methods sample from probability distributions to estimate posterior distributions and make predictions.
Methods and techniques in probabilistic computing
Methods and techniques used in probabilistic computing includes:
Bayesian networks: Bayesian networks, also known as probabilistic graphical models, represent probabilistic dependencies among variables using directed acyclic graphs. They enable efficient inference and reasoning under uncertainty in complex systems.
Markov Chain Monte Carlo (MCMC): MCMC methods, such as Metropolis-Hastings and Gibbs sampling, generate samples from the posterior distribution of model parameters. These samples are used to approximate posterior distributions and compute posterior expectations.
Variational Inference (VI): VI approximates the posterior distribution by optimizing a parametric approximation, such as a mean-field variational distribution. VI is computationally efficient and scalable to large datasets and complex models.
Probabilistic programming languages: Probabilistic programming languages, including Pyro, Stan, and Edward, provide a framework for specifying and manipulating probabilistic models. These languages enable flexible model specification, automatic inference, and uncertainty quantification.
Applications of probabilistic computing
Probabilistic computing has wide-ranging applications across various domains, including:
Machine learning: Probabilistic models are used for regression, classification, clustering, and generative modeling tasks. They enable uncertainty estimation, strength to noisy data, and principled integration of prior knowledge.
Decision making: Probabilistic models support decision-making under uncertainty in domains such as healthcare, finance, and robotics. They enable risk assessment, resource allocation, and adaptive decision-making strategies.
Natural Language Processing (NLP): Probabilistic models are used for tasks such as language modeling, machine translation, and speech recognition. They enable uncertainty-aware predictions and probabilistic reasoning over text data.
Sensor fusion: Probabilistic methods are used for sensor fusion in robotics and autonomous systems. They integrate data from multiple sensors and sources to estimate the state of the environment and make informed decisions.
Anomaly detection: Probabilistic models are used for anomaly detection in cybersecurity, fraud detection, and fault diagnosis. They identify deviations from expected behavior and detect abnormal patterns in data.
Challenges and future directions
Despite its advantages, probabilistic computing faces several challenges and opportunities for future research:
Scalability: Developing scalable algorithms and methods for inference and learning in large-scale probabilistic models.
Interpretability: Enhancing the interpretability of probabilistic models and uncertainty estimates to facilitate trust and understanding in decision-making systems.
Integration with deep learning: Integrating probabilistic methods with deep learning techniques to enable uncertainty-aware predictions and model robustness.
Real-world applications: Applying probabilistic computing techniques to real-world problems in domains such as healthcare, finance, and climate science.
Conclusion
Probabilistic computing offers a principled and flexible approach to modeling uncertainty, reasoning under uncertainty, and making informed decisions in complex and uncertain environments. With its foundations in probability theory, Bayesian inference, and probabilistic programming, probabilistic computing provides powerful tools for addressing challenges in artificial intelligence, machine learning, and decision-making. As research in this field continues to advance, probabilistic computing will play an increasingly important role in enabling intelligent systems to understand, reason, and act in uncertain and dynamic environments. Through ongoing innovation and collaboration, probabilistic computing will continue to shape the future of AI and computational intelligence.Citation: Williams D (2024) Towards Intelligent Decision-Making: Advancing Probabilistic Computing for Real-World Applications. Int J Swarm Evol Comput. 13:373.
Copyright: © 2024 Williams D. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.