Indexed In
- Open J Gate
- Genamics JournalSeek
- Academic Keys
- JournalTOCs
- ResearchBible
- China National Knowledge Infrastructure (CNKI)
- Scimago
- Ulrich's Periodicals Directory
- Electronic Journals Library
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- SWB online catalog
- Virtual Library of Biology (vifabio)
- Publons
- MIAR
- Scientific Indexing Services (SIS)
- Euro Pub
- Google Scholar
Useful Links
Share This Page
Journal Flyer
Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Research Article - (2021) Volume 12, Issue 4
Theoretical modeling and experimental validation of Electrical conductivity for highly aligned single-walled carbon nanotube thin films
Maher S. Amer*, Mark J. Foster, Ali M. Al Mafrage and Mohammed K. MohammedReceived: 15-Apr-2021 Published: 29-Apr-2021, DOI: 10.35248/2157-7439.21.9.565
Abstract
A new model capable of accurately predicting the electrical conductivity of highly aligned single-walled carbon nanotube thin films has been developed. The films ranged between 1 and 11 layers thick. The well-established Lamination theory failed to predict the experimentally measured values for the films of different thicknesses. However, this model, based on modified and expanded techniques applied within the realm of the lamination theory, could predict the exact values taking into consideration the inter-layer interaction that is crucial for the properties and performance of nano- films.
Keywords
Single-walled carbon nanotube (SWCNT); Carbon Nanotubes (CNTs); Thin Films; Electrical Conductivity; Langmuir-Blodgett (LB); Nanotubes; Lamination Theory; Modelling; Nanofilms.
Introduction
The excellent conductivity of CNTs attracts the intension for many industries. CNTs can be used to improve the conductivity of the polymer matrix due to its intrinsic electronic structure [1,2]. Composites designed with carbon nanotubes through various methods have displayed the ability to impact the electrical conductivity compared to a pure material [3]. Reinforced graphene materials with carbon nanotube composites are such a composite that has measured an increased ability for electrical conductivity [4,5]. Nanocomposite foams composed of carbon nanotubes had been produced through injection-molding [6]. The foams displayed similar conductivities away from the gate near the injection site. Near the gate, the electrical conductivity was consistently low. The study may display an explanation for this phenomenon. The conductivity has been measured to be dependent on the thickness of thin films [7]. Carbon-fiber laminate materials enhanced with aligned carbon nanotubes improve the electrical conductivity [8]. These studies have displayed the electrical conductivity of a material can be improved and impacted through the utilization of carbon nanotubes.
The electrical conductivity of thin films has been measured to be dependent on the design of the material. In which, multiple layered thin films made of polymer films has been measured to be dependent on the number of layers [9]. Also, this study determined that the electrical conductivity increases with increasing the number of layers through spin-coating multiple thin layers onto the substrate. Further studies display the electrical properties of carbon nanotubes have dependence on temperature [10].
Modeling or simulation of the mechanical properties of single-walled carbon nanotubes has been completed [11]. This model used the stiffness matrix to determine mechanical properties. The electromechanical properties have been modeled through finite element analysis for smart medical devices [12] as well as improving the electrochemical properties of thin-film composites [13].
In this work, the conductive properties will be modeled with the utilization of the experimental data with lamination theory methods. Research has displayed the electrical conductivities at the nanoscale is complicated and is not easy to achieve [14]. However, this study successfully produced a monolayer of well-aligned SWCNTs monolayer, measured the electrical conductivities of highly aligned single-walled carbon nanotubes, and demonstrates a method to determine the electrical conductivities in both theoretical and experimental approaches.
Materials and Methods
Theoretical approach: The electrical conductivity of single-walled carbon nanotubes was analyzed using MATLAB. The arrangement of multilayered single-walled carbon nanotube films with the variation of the layer orientation was analyzed through analogous and expanded techniques from the lamination theory represented in Mechanics of Fibrous Composites for determining mechanical properties of multilayered thin-film composites. Conductive property analysis of thin-film composites depending on the angle orientation of each layer, and the total number of layers can be determined with the analysis within this study.
The material is assumed to be homogenous and orthotropic. The orthotropic assumption allows the material to be defined as having different material properties in different orthogonal directions. The material is assumed to be linear, and any mismatch of other stresses or conductive properties are assumed to not affect the entire composite. Symmetry about the origin is generally assumed for simplicity.
The conductivity of a material can be modeled as a [3 x 3] tensor matrix. Equation 1 is an example of the electrical conductivity tensor, [σ], in x, y, and z directions.
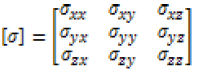 (1)
(1)
Single-walled carbon nanotubes have orthotropic properties; therefore, the conductivity tensor analyzed in the x, y, and z directions can be represented as the conductivities as the axial, transverse, and radial directions. The conductivity tensor for single-walled carbon nanotubes is reduced due to the material being orthotropic. The reduced electrical conductivity tensor is the diagonal tensor equation 2, where the 1, 2, and 3 directions represent the axial, circumferential, and radial directions. Transformation tensors, equations 3-4 [15], are used to determine a film’s properties based on the film being oriented in the direction θ.
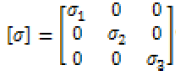 (2)
(2)
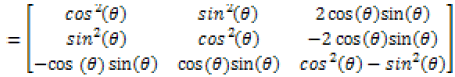 (3)
(3)
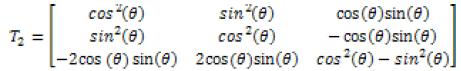 (4)
(4)
Experimental approach
Highly purified Luna ® single-wall carbon nanotubes powder, which contains less than 1 weight percent of metal catalyst remaining in them, is used in our experimental work. To characterize the used CNTs several tests are applied to get the precise details related to their names, structure, Raman spectroscopy, high-resolution transmission electron microscopy, and scanning tunneling microscopy. N, N-dimethylformamide (DMF) (Fisher Scientific, reagent grade) is used as a solvent with Deionized water (ASTM type II) as a subphase during the Langmuir-Blodgett deposition. After producing the CNT’s solution, different sonication times starting from 20 minutes till six and half hour by using a 60 MHZ ultrasonic bath (Fisher Scientific, Model FS20) was applied. A centrifuged (Beckman Coulter, Allegra TM X22R) for 30 minutes at 12000 RPM was used to centrifuge the sonicated solution. The concentration of SWCNTs in pure centrifuged saturated solutions was measured using the gravimetric method and was found to be 0.046 mg/ml based on ten measurements using a balance with 0.1mN sensitivity [14,16]. A SWCNT’s monolayer films were assembled by using a Langmuir-Blodgett (LB) trough (Nima Technology UK, 1222D2) in a class 100 level clean enclose.
After optimizing the sonication time, quantity add to the trough and evaporation time a monolayer of SWCNTs can be produced by using 1000 μl of solution (DMF and SWCNTs) sonicated for 3 hours then centrifuged for 30 minutes, finally left to evaporate the solvent for 30 minutes after spreading the solution on the subphase surface in the trough of 500 cm2 [14].
The produced monolayer was deposited on a glass slide substrate for further investigation of their electrical properties. In addition to that, films of three, five, seven, and eleven layers were also deposited to study their electrical properties. A semiconductor parametric analyzer (Keithley 2401, Keithley Instruments Inc., Cleveland, OH) that can measure current and voltage with a resolution of pA and μV, respectively was used to measure electrical conductivity, with 4-point probe measurements in which the current pass through the outer probes and the voltage drops between the middle probes and the resistance measured automatically by the Keithley device by using the I-V computer software.
Results and Discussion
Because all experimental measurements were conducted in the plane, the electrical conductivity tensor was reduced to the axial and transverse directions, [αr], displayed as equation 5. This is completed due to the orthotropic assumption, and this equation is used to determine individual layer’s conductivity, equation 6, of a multilayer composite [α]i, or the conductivity of the ith layer of a laminate.
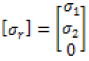 (5)
(5)
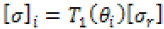 (6)
(6)
The conductivity varies based on the orientation of the individual layer. The least distance to conduct due to the cylindrical profile of single-walled carbon nanotubes is the axial direction and has the greatest conductive properties [15-17]. Figure 1 displays the axial and transverse electrical conductivities of a single layer of highly oriented single-walled carbon nanotube film in two dimensions for all directions. Axial and transverse conductivities are displayed as σy and σx, respectively. The [0] oriented conductivities are calculated as 29,000 & 20,000 S/cm for the axial and transverse directions, respectively. (Figure 1)
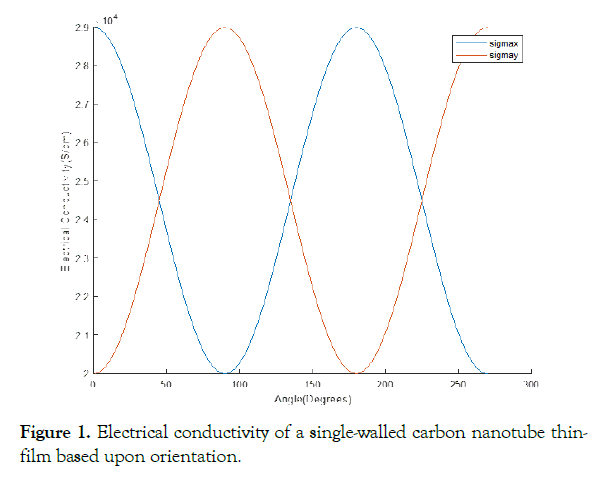
Figure 1. Electrical conductivity of a single-walled carbon nanotube thin-film based upon orientation.
The electrical conductivity of a multilayered thin films was determined by expanding the lamination theory protocol. The subscript “c” will be used to denote conductive calculations based upon the lamination theory. The reduced conductive matrix, Qc, is displayed as equation 7, and the reduced transformed matrix can be determined through equation 8 and the transformation matrices. Equation 9 and 10 formulate each individual layer’s laminate in-plane conductivity and conductivity, respectively, where z is the thickness of each layer. Equations 11 & 12 calculate the film in-plane electrical conductivity and the mid-plane electrical conductivity, respectively.
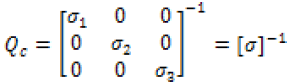 (7)
(7)
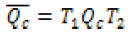 (8)
(8)
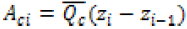 (9)
(9)
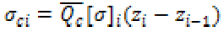 (10)
(10)
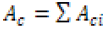 (11)
(11)
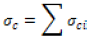 (12)
(12)
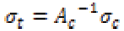 (13)
(13)
Equation 13 calculates the film’s conductivity as a whole.
The conductivities of multilayered films with each individual layer being oriented in the same direction is hypothesized to have the conductivity of the original single-layered thin film. Methods to determine the conductivities of multilayered films were applied for composites oriented in the same direction. The individual layer and a composite composed of 2 layers have overall conductivities that are determined identically through this method.
Calculations of an 11-layer single-walled carbon nanotube thin film with a [0] degree orientation for all layers was conducted. This calculation, through this method, is displayed in Figure 2. The identical result was found for both the two layers and eleven layers and equated to the conductivity of one layer, which is displayed in figure 2 where the two calculations overlap in the figure. This calculation displays that according to the bulk lamination theory, the conductivity does not depend on the number of layers of the film.
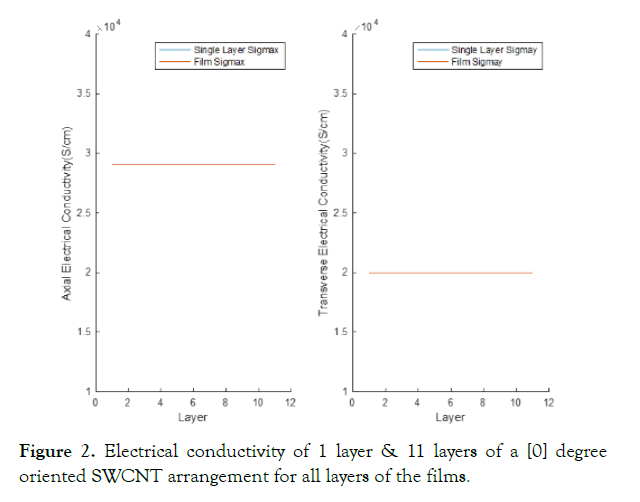
Figure 2. Electrical conductivity of 1 layer & 11 layers of a [0] degree oriented SWCNT arrangement for all layers of the films.
The electrical conductivity of multilayered single-walled carbon nanotubes has been determined through experimental analysis by using the Langmuir-Blodgett technique [14]. This research contradicts results predicted through previous calculations that the conductivity is independent of the number of layers. Therefore, a correction factor must be prepared to determine the true conductivity of a multilayered composite and that the electrical conductivity of single-walled carbon nanotubes has a dependency on the number of layers.
Ali et al. [18] by using the Langmuir-Blodget technique, studied the electrical conductivity of the SWCNT films as a function of number of layers figures 3-5. The electrical conductivity through this data has a clear dependency on the number of layers.Therefore, a different method must be determined and implemented to calculate the true electrical conductivity of such multilayered thin films.
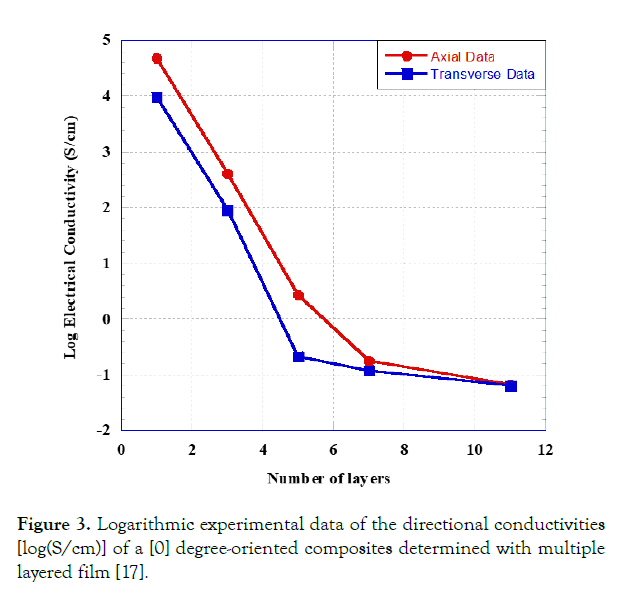
Figure 3. Logarithmic experimental data of the directional conductivities [log(S/cm)] of a [0] degree-oriented composites determined with multiple layered film [17].
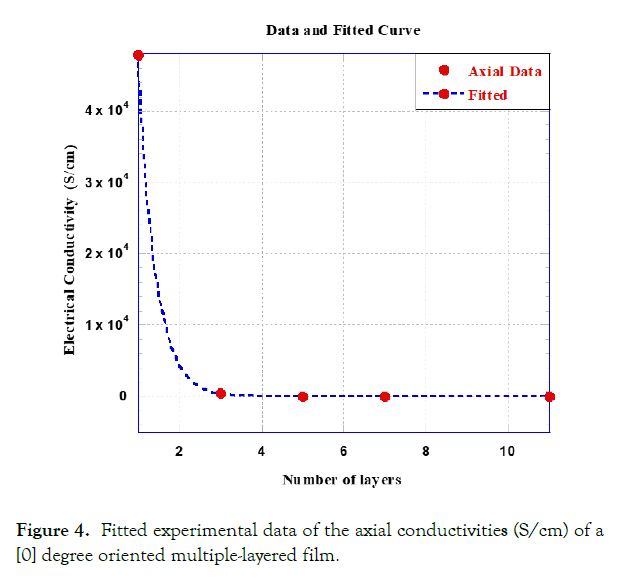
Figure 4. Fitted experimental data of the axial conductivities (S/cm) of a [0] degree oriented multiple-layered film.
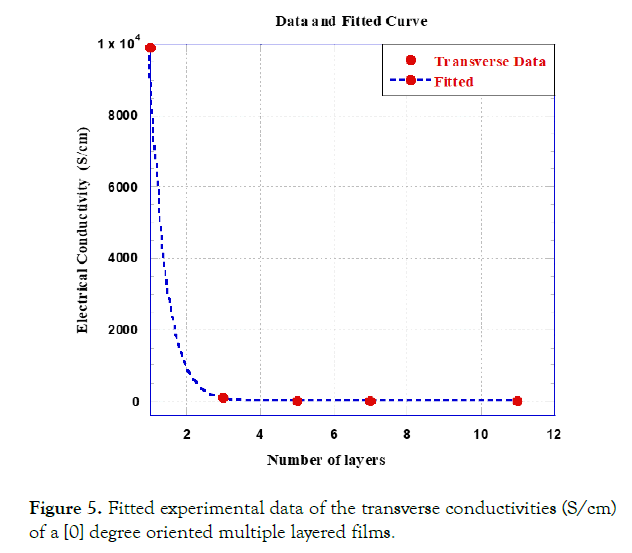
Figure 5. Fitted experimental data of the transverse conductivities (S/cm) of a [0] degree oriented multiple layered films.
The reduced electrical conductivity tensor in the [0] direction based upon the assumption that the material is orthotropic is displayed in equation (14) or [σ][0] where the superscript denotes the angle orientation.The direction conductivities σ1 and σ2 represent the directional electrical conductivities in the axial and transverse directions, respectively, of one single layer of the material-oriented in the [0] direction.
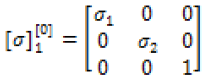 (14)
(14)
The correction factor in tensor form as a function of the number of layers, n, is determined with the data from the experimental study [14] and through computations in MATLAB. Equation 15 calculated the correction factor [cf]n, for highly aligned single walled carbon nanotubes from the experimental data.
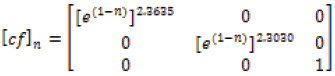 (15)
(15)
Where n is the number of layers of the composite, therefore the true electrical conductivity can be calculated through this method and is a function of the number of layers n, equation (16).
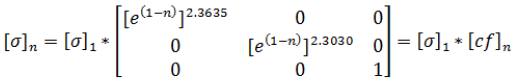 (16)
(16)
Equations (17-21) represent the calculated correction factor tensors for one to five layers of single-walled carbon nanotubes determined to four significant digits determined from formulas stated previously.
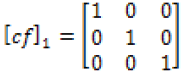 (17)
(17)
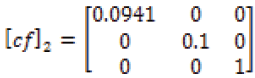 (18)
(18)
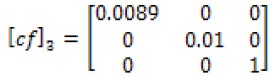 (19)
(19)
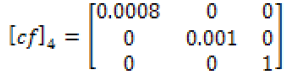 (20)
(20)
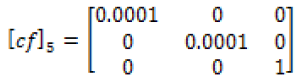 (21)
(21)
It is worth noticing here, the correction factor tensor of one layer is the identity matrix. The subsequent correction factors of greater than 6 layers have significant digits greater than five, and therefore the corrections factor tensors of five layers or less are displayed only. Equations (22-26) are the electrical conductivity equations for single-walled carbon nanotubes with layers 1-5, respectively.
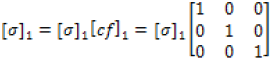 (22)
(22)
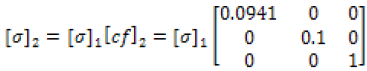 (23)
(23)
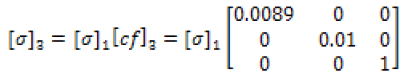 (24)
(24)
 (25)
(25)
 (26)
(26)
Figures 6 and 7 display the electrical conductivities calculated through these methods for different layered single-walled carbon nanotubes compared to the in lab experimental data [14]—The calculated based upon the modeled transverse and axial electrical conductivities and transforming the data with transformation tensors.
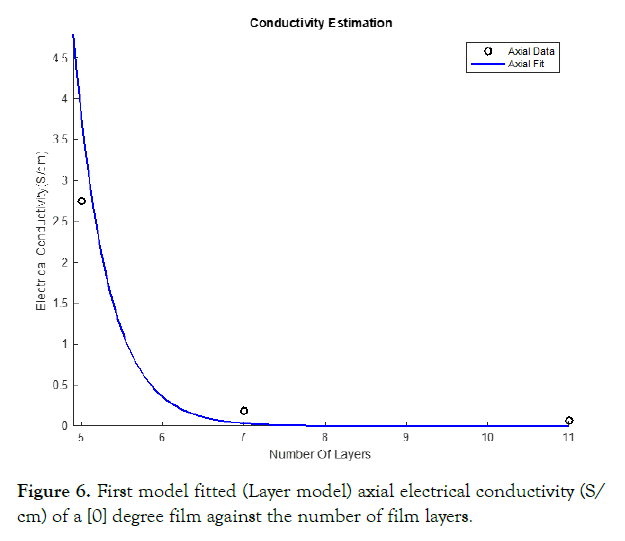
Figure 6. First model fitted (Layer model) axial electrical conductivity (S/ cm) of a [0] degree film against the number of film layers.
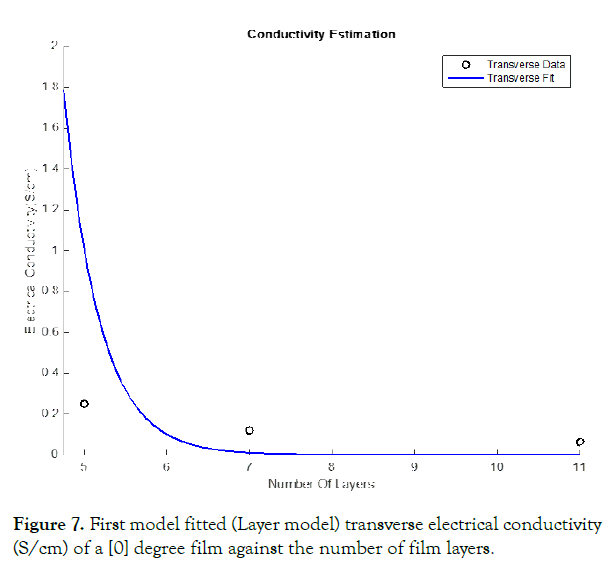
Figure 7. First model fitted (Layer model) transverse electrical conductivity (S/cm) of a [0] degree film against the number of film layers.
This method of estimating the electrical conductivity proves the experimental data does not match exactly with the model as increasing the number of layers of the film. Investigating the data compared to the model more closely visualizes the difference of the model against the experimental data. (Figures 8-12) visualize the differences of the model to the in-lab measurements.
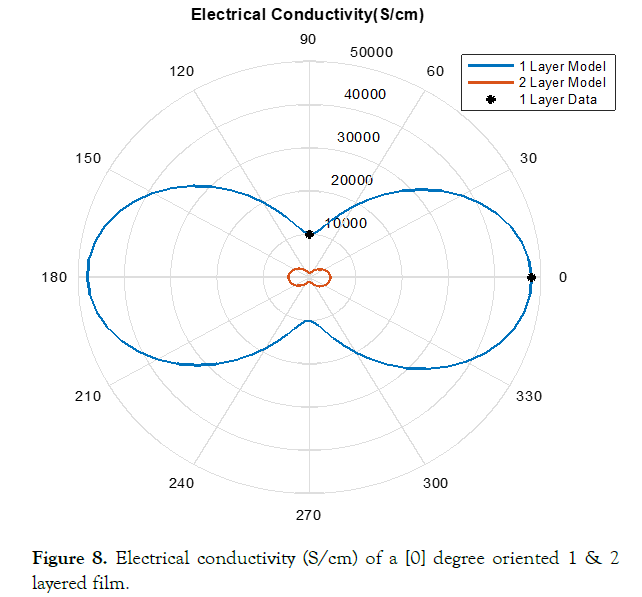
Figure 8. Electrical conductivity (S/cm) of a [0] degree oriented 1 & 2 layered film.
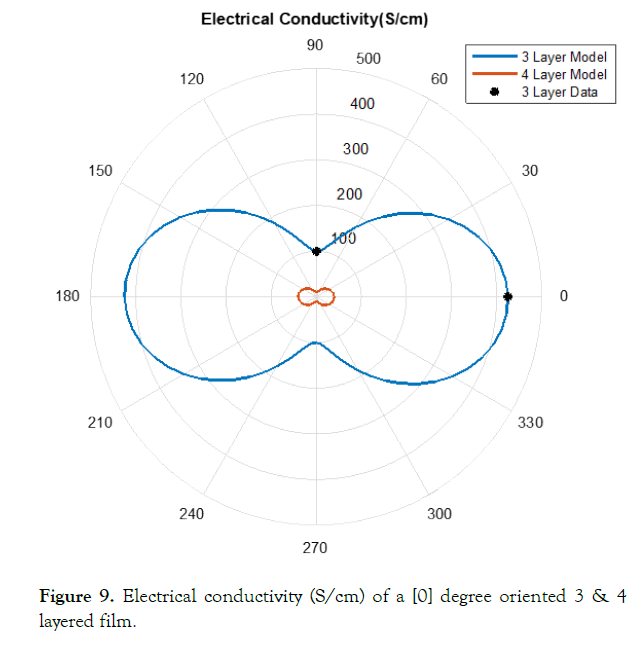
Figure 9. Electrical conductivity (S/cm) of a [0] degree oriented 3 & 4 layered film.
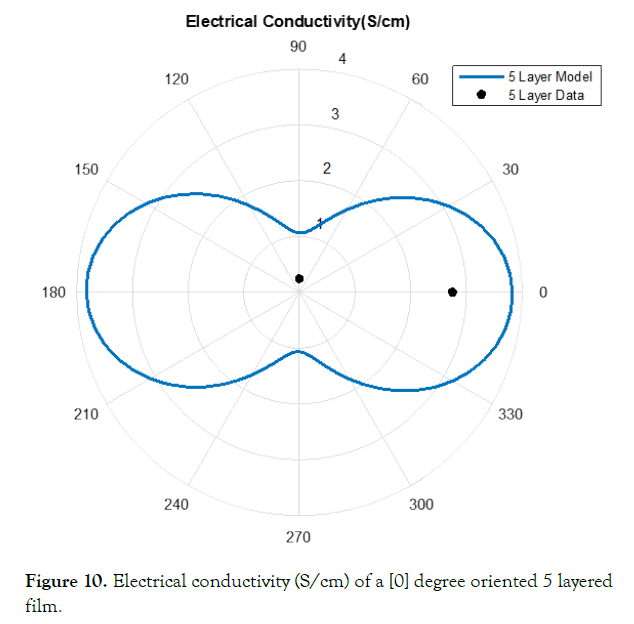
Figure 10. Electrical conductivity (S/cm) of a [0] degree oriented 5 layered film.
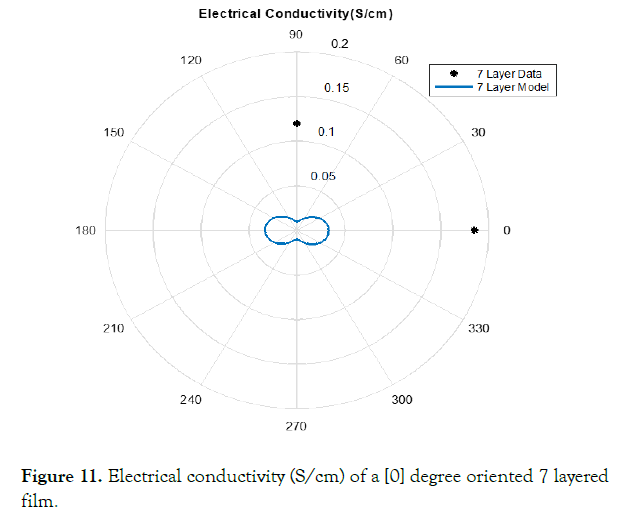
Figure 11. Electrical conductivity (S/cm) of a [0] degree oriented 7 layered film.
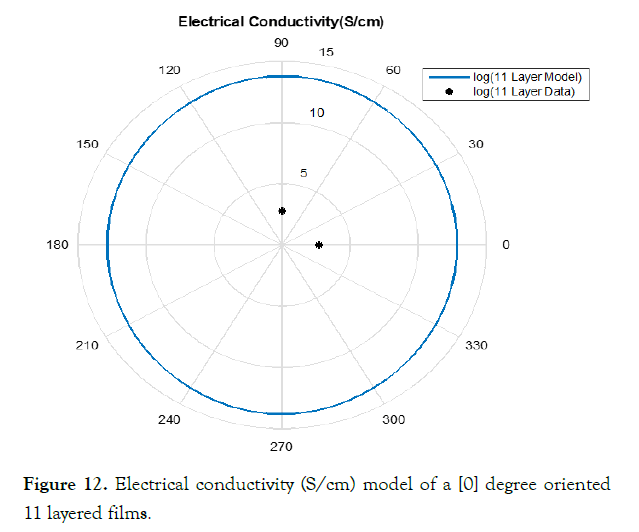
Figure 12. Electrical conductivity (S/cm) model of a [0] degree oriented 11 layered films.
The model designed in equation 16 approaches 0 with the increasing number of layers of the films. This model predicts conductivity on the order of 10-6 S/cm at 11 layers. Due to the increasing error with the increasing of the number of layers, improvement to the model is necessary. The addition of infinite conduction to the model improves the error previously discovered. Equation (27) improves the accuracy of equation (16) where [e] ∞a and [e]∞t are the infinite conductivities in the axial and transverse directions, respectively. For the sake of this model, the experimental data taken for 11 layers will be used as our infinite conduction values for the model. Figures 13 and 14 display the improvement in the electrical conductivities calculated through this model for different layered single-walled carbon nanotubes compared to the in lab experimental data. This model, with the addition of the infinite conduction to correction factor, proves a better fit to the experimentally measured data, especially at 7 layers and greater.
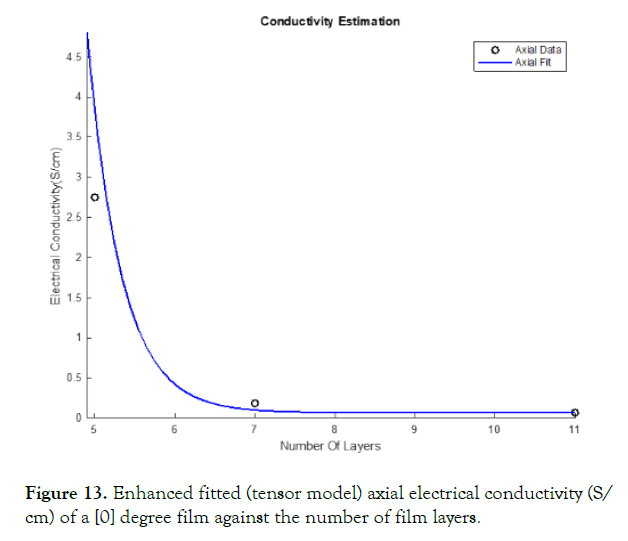
Figure 13. Enhanced fitted (tensor model) axial electrical conductivity (S/ cm) of a [0] degree film against the number of film layers.
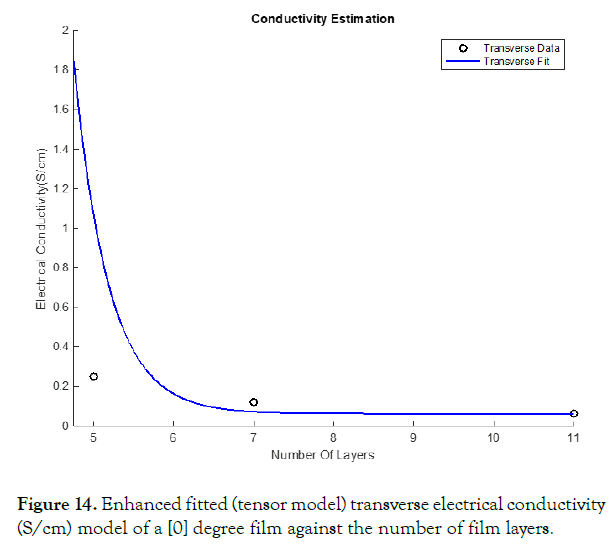
Figure 14. Enhanced fitted (tensor model) transverse electrical conductivity (S/cm) model of a [0] degree film against the number of film layers.
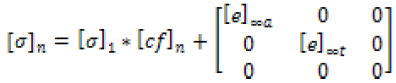 (27)
(27)
The correction factor calculated based upon the data was completed through equations (28-32). Figures 15-19 display this accuracy of these models based upon the in experimental lab data
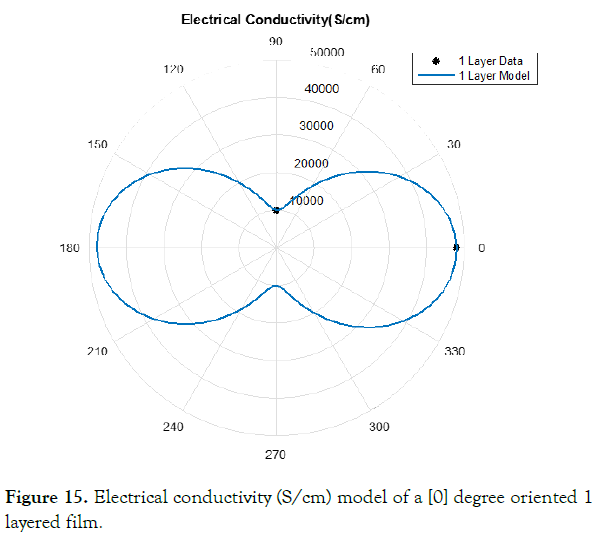
Figure 15. Electrical conductivity (S/cm) model of a [0] degree oriented 1 layered film.
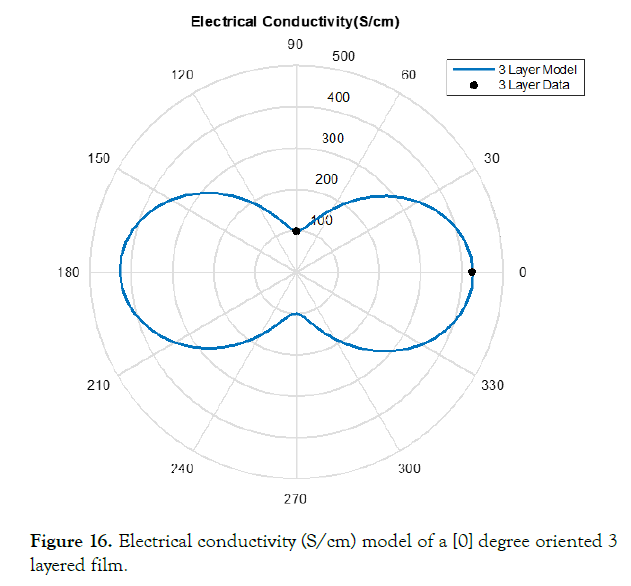
Figure 16. Electrical conductivity (S/cm) model of a [0] degree oriented 3 layered film.
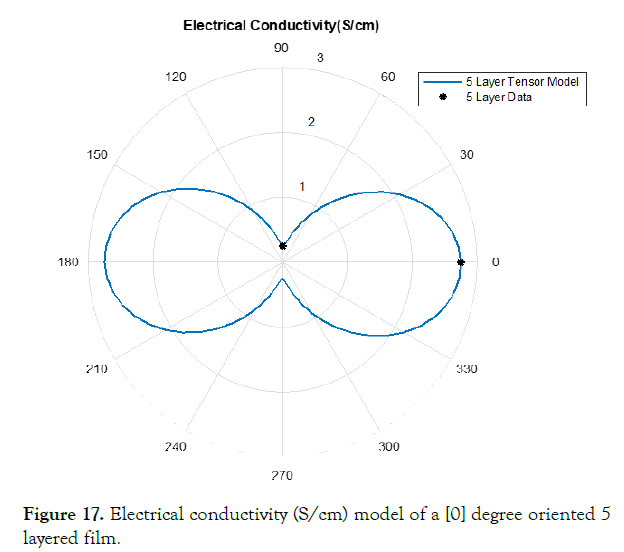
Figure 17. Electrical conductivity (S/cm) model of a [0] degree oriented 5 layered film.
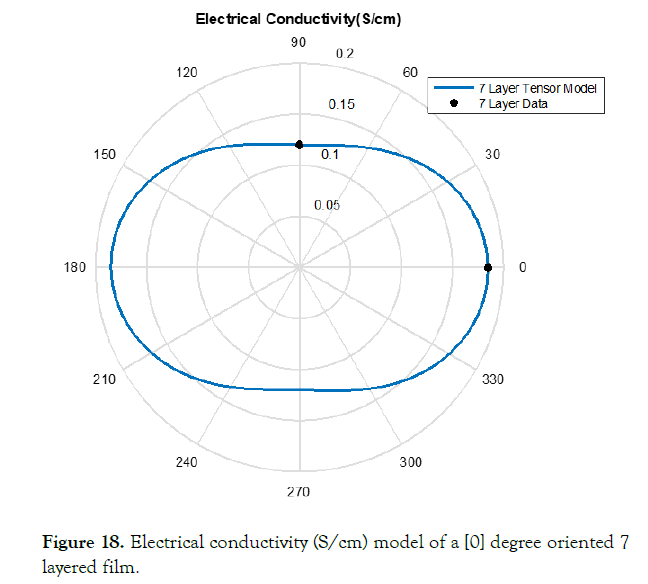
Figure 18. Electrical conductivity (S/cm) model of a [0] degree oriented 7 layered film.
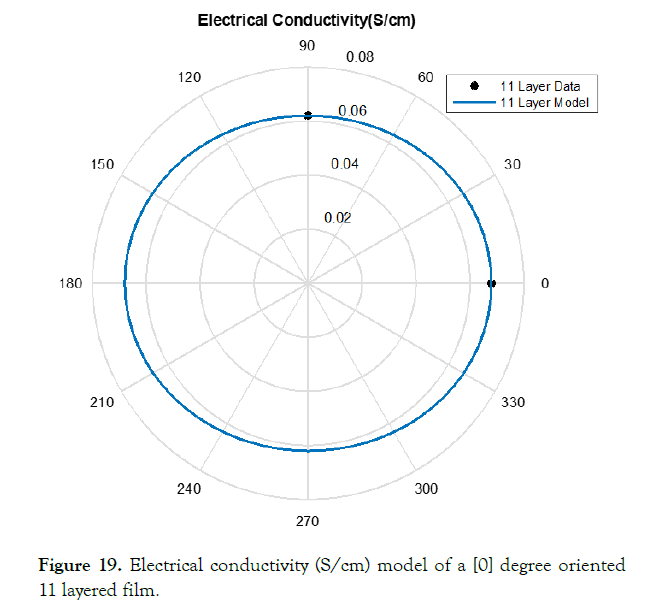
Figure 19. Electrical conductivity (S/cm) model of a [0] degree oriented 11 layered film.
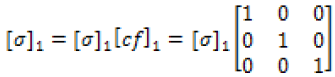 (28)
(28)
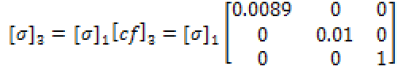 (29)
(29)
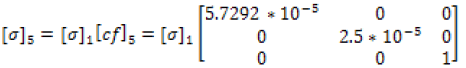 (31)
(31)
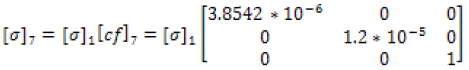 (32)
(32)
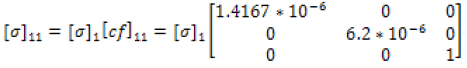 (33)
(33)
Conclusion
The conductivity of multilayered SWCNT films can be determined using methods generated within this study. The properties of a specific material can be determined through this methodology and can be used for a variety of different applications. Singlewalled carbon nanotubes can display properties vastly different to metals, ceramics, and polymers. Composites embedded with single-wall carbon nanotubes could have several applications in the nanotechnology field due to the stimulating physical properties.
These methods of calculating respective conductive properties of can be used for other nanofilms.
Funding
This research received no external funding.
Acknowledgments
This research has no acknowledgment.
Conflicts of Interest
The authors declare no conflict of interest
REFERENCES
- Cai W, Li M, Wang S, Gu Y, Li Q. Strong, flexible and thermal-resistant CNT/polyarylacetylene nanocomposite films. RSC Adv. 2016;(6)4077-4084.
- Tsonos C, Tomara G, Yang B, Soin N, Psarras G. Electromagnetic waveabsorption properties of ternary poly(vinylidene fluoride)/magnetite nanocomposites with carbon nanotubes and graphene. RSC Adv. 2016;(6)1919-1924.
- Wang Y. Mechanical and electrical enhancement of super-aligned carbon nanotube film by organic and inorganic doping. Nanotechnology. 2019;31(7): p. 075601.
- Kwon YJ, Kim Y, Jeon H, Cho S, Lee W. Graphene/carbon nanotube hybrid as a multi-functional interfacial reinforcement for carbon fiber-reinforced composites. Composites Part B:Engineering. 2017;122, 23-30.
- Cui K, Maruyama S. Multifunctional graphene and carbon nanotube films for planar heterojunction solar cells. Progress in Energy and Combustion Science. 2019;70: p. 1- 21.
- Ameli A, Kazemi Y, Wang S, Park CB, Pötschke P. Process-microstructure-electrical conductivity relationships in injection-molded polypropylene/carbon nanotube nanocomposite foams. Composites Part A: Applied Science and Manufacturing. 2017;96,28-36.
- Rajanna P.M, Gilshteyn E.P, Yagafarov T, Aleekseeva A.K, Anisimov A.S et al. Enhanced efficiency of hybrid amorphous silicon solar cells based on single-walled carbon nanotubes and polymer composite thin film. Nanotechnology. 2018;29.
- Russello M, Diamanti EK, Catalanotti G, Ohlsson F, Hawkins SC. Enhancing the electrical conductivity of carbon fibre thin-ply laminates with directly grown aligned carbon nanotubes. Composite Structures. 2018;(206)272-278,
- Andrei V, Bethke K, Madzharova F, Beeg S, Knop-Gericke A. Size Dependence of Electrical Conductivity and Thermoelectric Enhancements in Spin-Coated PEDOT:PSS Single and Multiple Layers. Advanced Electronic Materials 2017;(3).10.1002.
- Ichkitidze LP, Gerasimenko AY, Podgaetsky VM, Selishchev SV, Dudin AA. Electrical Conductivity Of the Nanocomposite Layers For Use In Biomedical Systems. Materials Physicsand Mechanics.2018;(37)140-145.
- El Moumen A, Tarfaoui M, Hassoon O, Lafdi K, Benyahia H. Experimental Study and Numerical Modelling of Low Velocity Impact on Laminated Composite Reinforced with Thin Film Made of Carbon Nanotubes. Applied Composite Materials. 2018;(25)309-320.
- ZhaoY, Schagerl M, Viechtbauer C, Loh KJ. Characterizing the Conductivity and Enhancing the Piezoresistivity of Carbon Nanotube-Polymeric Thin Films. Materials (Basel). 2017;(10)724.
- Dettlaff A, Sawczak M, Klugmann-Radziemska E, Czylkowski D, Miotk R. High-performance method of carbon nanotubes modification by microwave plasma for thin composite films preparation. RSC Adv. 2017;(7)31940-31949.
- Al Mafarage A.M. Processing and Properties of Multifunctional Two-Dimensional Nanocomposite Based on Single Wall Carbon Nanotubes. Wright State University. 2019.
- Herakovich C.T. A Concise Introduction to Elastic Solids. Mechanics of fibrous composites. 1998.
- Amer M.S, Busbee J.D. Self-Assembled Hierarchical Structure of Fullerene Building Blocks Single-Walled Carbon Nanotubes and C60. J Phys Chem C. 2011;(115)10483- 10488.
- Song Y.S, Youn J.R. Evaluation of effective thermal conductivity for carbon nanotube/polymer composites using control volume finite element method. Carbon. 2006;(44)710- 717.
- Amer M, Mafarage A, Mohammed M. Compressive Mechanical Behavior of Highly-Aligned Monolayer Films of Single-Walled Carbon Nanotubes Using Langmuir-Blodgett Technique. J Nanom Nanos Tech. 2019;109.
Citation: Amer MS, Foster MJ, Mafrage AMA, Mohammed MK (2021) Theoretical modeling and experimental validation of Electrical conductivity for highly aligned single-walled carbon nanotube thin films. J Nanomed Nanotech. 12: 565.
Copyright: © 2021 Amer MS, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.