International Journal of Swarm Intelligence and Evolutionary Computation

The Social Significance of Network Structural Optimizations

Haifeng Du^*, Xiaochen He and Yang Wang School of Public Policy and Administration, Center for Administration and Complexity Science of Xi’an, Jiao Tong University, Xi’an, Shanxi Province, 710049, China
^*Correspondence: Haifeng Du, School of Public Policy and Administration, Center for Administration and Complexity Science of Xi’an, Jiao Tong University, Xi’an, Shanxi Province, 710049, China, Email:

Received: 29-Apr-2020 Published: 20-May-2020, DOI: 10.35248/2090-4908.20.9.183

Description

Network structure plays a fundamental role in dynamical processes including spreading phenomena, synchronization, percolation, etc. It is critical to optimize the network topological structure as it is highly related to engineering problems and has substantial societal impacts. Thanks to the development of network science, comprehensive mathematical tools, and artificial intelligence in the last decade, problems related to structural optimization have attracted much research, including minimize the average path length [1], and transforming networks into balanced or small-world ones with the lowest cost [2,3]. What about the network diameter, which often describes the transfer efficiency of a team or a crowd [4] In 2017, we studied the relationship between the network diameter and the number of edges added to the network, finding that there exists a critical point beyond which the average path length decreases linearly and the network diameter changes abruptly from three to two [5]. With the diameter reaches to the critical point, the efficiency of information sharing could be substantially enhanced. As a result, we attributed the network diameter at the critical point as the Critical Diameter [5].

Given the importance of the network diameter to the dynamical processes, the next question is to achieve the Critical Diameter by adding the minimum number of links to the network, which is an NP-hard problem [5] .Brute-force search algorithm often, requires (N^{^2k+3}) where k is the number of edges added to the network, which cannot be generalized to large networks. As a result, we designed a mimetic algorithm that provides among the first solution to this optimization problem [5]. By comparing the mimetic algorithm with two additional algorithms: 1) Connecting links between the highest-degree nodes with all other nodes (denoted by HDN), and 2) Greedy algorithm, we found the mimetic algorithm balances the time complexity and generalizability.

What is the implication? What can we learn from this optimization problem? To provide actionable suggestions, this study is towards an important step to inform policy makers to design optimal network structure or intervene specific events. It provides the following suggestions: In a centralized environment with limited resources, the study suggests that the best way to enhance the transfer efficiency or the information sharing speed is to connect the hub with other nodes. For example, if the aim is to build roads in a remote rural area, connecting hubs with other places is the optimal way. Additionally, connecting opinion leaders with other individuals in social networks is commonly used for managers. For example, the best way to accelerate the diffusion of innovations is to find the opinion leaders who can help spread the information to more consumers [6]. However, in a dense network where resources are abundant; a decentralized operation may have its practical significance. For instance, if we aim to build roads in a developed city, a multicenter strategy may be a good way to improve the transportation efficiency.

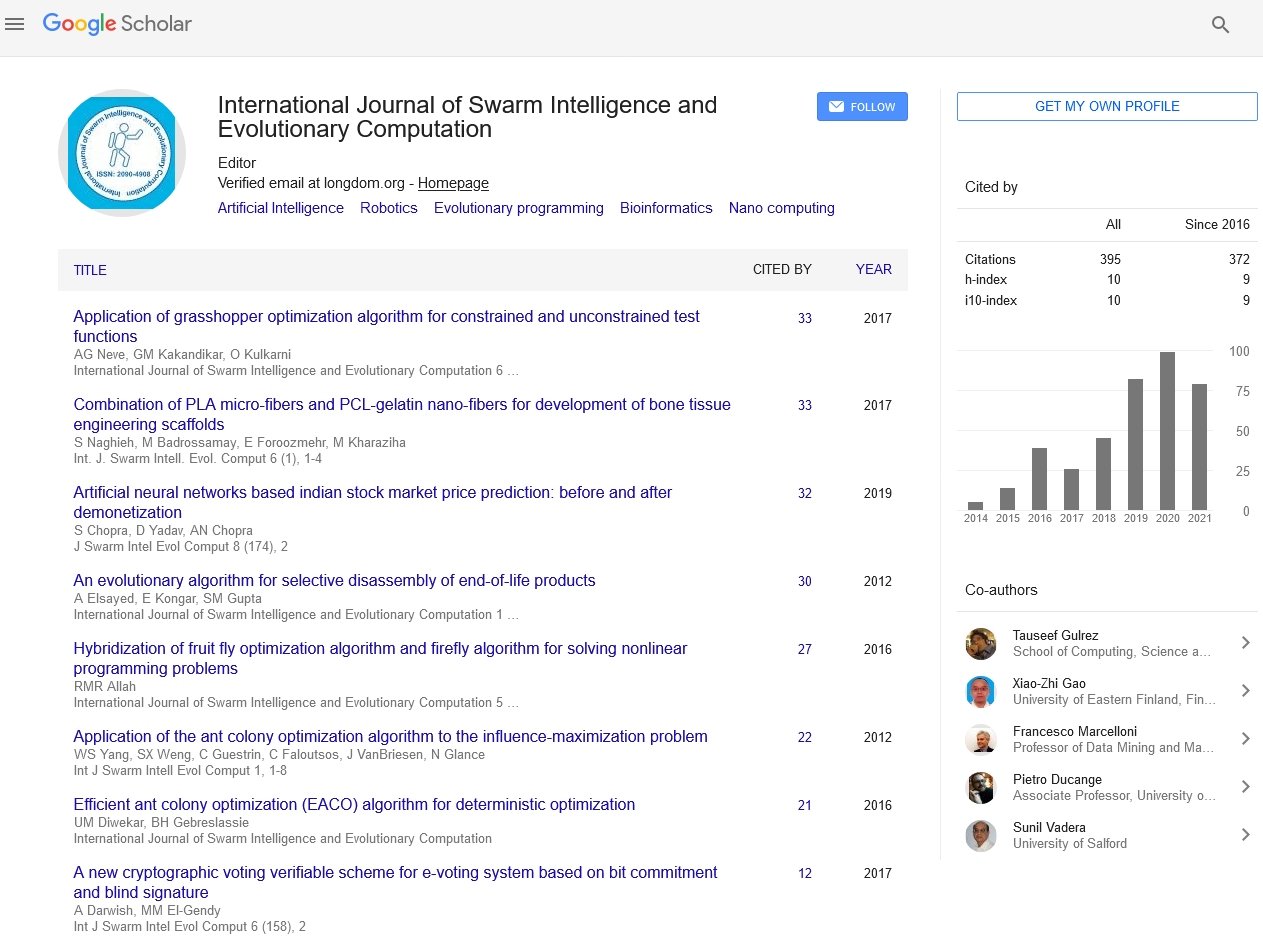
The other application of the optimization problem is the analysis of collective action [7], which has great implications both for individuals and policy makers. Specifically, we apply the optimization algorithm in [8] to an investigated Chinese rural migrant worker’s informal social network (Figure 1) Since the network shows clear community structure (colors represent communities; individuals within communities communicate with each other more frequently than those in different communities), the collective action is likely to be launched within communities, while members in other communities hardly get this information. For example, when node 33 in color blue launches a protest, node 60 does not get the information immediately. As a result, the collective action occurs locally. However, the contagion process significantly accelerates as the network reaches the Critical Diameter. Interestingly, we find that the mimetic algorithm yields the same network structure as the HDN method, which explains the resource mobilization theory [9]. According to the theory, launchers of the collective action are always the opinion leaders who have plenty of resources. When someone in the crowd experiences an inequality, he/she turns to the leader (node 12) for the protest, while the optimized network may enlarge the mobilized resources and make the protest into a bigger scale. Optimizing the critical diameter may be a potential risk for promoting the collective action, but on the other side we can also speculate that the hub node can be also the key person to impede from the collective action’s happening.

Figure 1: Original and optimized topologies of the rural migrant worker’s social network.

The size of nodes represents the node degree. The different nodes’ colors represent the different clusters computed by the modularity. The black lines denote the original network edges, while the red lines denote the added edges. (a) is the original network, while (b) is the optimized network with the critical diameter.

Optimizing network structure is critically for the dynamical processes and has potential policy implications. Developing algorithms that achieve the Critical Diameter by adding the minimum number of links is just one of the many essential steps toward this goal. We explore a possibility for exploring the optimization of critical diameter, but developing scalable algorithms for large social networks is still an open question. As the development of the artificial intelligence, how to incorporate this latest tool? What is more, what can AI guiding us to solve the optimization problem?

Conclusion

Finally, to uncover underlying social mechanisms of the optimization methods, we need to further discuss the relationship between the network density, scale, topological structure and the optimal edging strategies. With the opening of new data sources and tools, the answers to these questions will soon arrive; we hope the application of the optimization of the critical diameter into the social practice come true in the near future.

REFERENCES

1. Xuan Q, Li Y, Wu TJ. Optimal symmetric networks in terms of minimizing average shortest path length and their sub-optimal growth model. Physica A: Statistical Mechanics and its Applications. 2009;388:1257-1267.
2. Wang S, Gong M, Du H, Ma L, Miao Q, Du W. Optimizing dynamical changes of structural balance in signed network based on memetic algorithm. Social Networks. 2016;44: 64-73.
3. Du H, Fan J, He X, Feldman MW. A Genetic Simulated Annealing Algorithm to Optimize the Small-World Network Generating Process. Complexity. 2018.
4. Peng J, Xu G. Average path length for Sierpinski pentagon. arXiv preprint arXiv:1112.4943. 2011.
5. Du H, Wang J, He X, Du W. A memetic algorithm to optimize critical diameter. Swarm Evol Comput. 2019; 47: 56-65.
6. Valente TW, Davis RL. Accelerating the diffusion of innovations using opinion leaders. Ann Am Acad Pol Soc Sci. 1999;566 :55-67.
7. Sutter J. Penrose LS-On the Objective Study of Crowd Behaviour. Population 1953; 8: 174.
8. Göbel C.Social Unrest in China: A bird's eye perspective (Working Paper).2017.
9. McCarthy JD, Zald MN. Resource mobilization and social movements: A partial theory. Am J Soc. 1977; 82: 1212-1241.