Indexed In
- Open J Gate
- Genamics JournalSeek
- Academic Keys
- JournalTOCs
- ResearchBible
- China National Knowledge Infrastructure (CNKI)
- Scimago
- Ulrich's Periodicals Directory
- Electronic Journals Library
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- SWB online catalog
- Virtual Library of Biology (vifabio)
- Publons
- MIAR
- Scientific Indexing Services (SIS)
- Euro Pub
- Google Scholar
Useful Links
Share This Page
Journal Flyer
Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Research Article - (2021) Volume 12, Issue 5
The Flow of a Micropolar Nanofluid Past a Stretched and Shrinking Over Wedge Surface With Absorption
HA El-Dawy1* and Rama Subba Reddy Gorla22Department of Aeronautics and Astronautics, Air Force Institute of Technology, Wright Patterson Air Force Base, Dayton, Ohio, USA
Received: 04-Mar-2021 Published: 25-Mar-2021, DOI: 10.35248/2157-7439.21.12.561
Abstract
This research is examining, a continuous, laminar, flow of a micropolar nanofluid through a Stretched and shrinking in the heat generating or absorbing and magnetcfield over a wedge surface. A number of identical parameters are em ployed to aset of results and graphed by transforming the governing from partial differential equations into ordinary differential equations after solving the governing equations numerically by using the Runge Kutta Gill and shooting methods (fourth order. The steady-state velocity, temperature, and angular velocity profiles are shown graphically displayed. The result showed an effect of a nanoparticle, measure angle of the wedge, suction and material parameter in temperature, velocity, and angular velocity.
Keywords
Nanoparticle; Micro rotation; Thermophysical properties
Introduction
Recently, many studies have fluid flow over multiple surfaces, but in the last Ten years, many works have appeared to study Nanofluid flow over horizontal and vertical surfaces, due to the appearance of the important this study in our lives and more importance for engineering. There are many papers on micropolar fluids and heat transfer and many inquiries. Just, several works have proclaimed the importance of the impact of nanoparticles in many fields; in manufacturing, such as glass, in the military, solar and nuclear reactors. Nanoparticles also have effects in the human body as in the flow of urine in the kidneys and the bladder. The works which can define non-Newtonian fluid properties, many practical applications, such as plastic sheet extrusion, paper production, glass blowing, metal spinning, and plastic film drawing, depend on fluid dynamics on the stretching surface. Because of the wide complexity of non- Newtonian fluid physical construction, there is no particular framework in studies except some recent work in this direction. Micro polar fluids have gained considerable interest from researchers among the various models of non-Newtonian liquids. Since the equation governing the flow of a micro polar fluid involves a micro rotation vector and a gyration parameter in addition to the velocity vector area, the consistency of the final product is determined by the rate of heat transfer at shrinking and stretching surfaces, as well as other cases involving convection free flow. S.R. Mishra. A Mixed Forced H.A El-dawy. Small particles like powder, copper, aluminium, titanium, etc. The opposite force faces the temperature gradient If the temperature gradient is suspended in the gas, which is why it has many practical applications to remove small particles from the gas currents and study The particulate matter deposition on turbine blade.
Throughout this research, we are researching the effect of nanoparticles on over shrinking and stretching wedges throughout fluid flow, heat transfer and micro-rotation velocity. Nevertheless, there is one way to rising entropy generation as provided to find the optimal design for thermal systems with minimal energy loss available by Bejan [2]. This method has been widely applied to the problems of free and forced free pregnancies and has been proven in the literature [3-8,11-14]; the introspection generation has been mostly analyzed in containers filled with conventional fluids (eg water, ethylene glycol, etc.). The study of the flow of thermoplastic nanoparticles between parallel disks has been stimulated with particular attention to the last generation of entropy by Another study to analyze the generation of entropy in trapezoid microchannels of continuous laminar flow of pure water and CuO-water nanofluids. It reduces the entropy in the small channel, the optimal aspect ratio of the channel and the number of Reynolds numbers. Entropy generation was analyzed due to flow and heat movement in three different channels: nanotubes, small channels and the conventional channel with nano-fluid alumina-water as fluid models. Their findings showed whether high-viscosity alumina should be used as a refrigerant in small canals, small canals, and conventional channels or not based on the flow system. It also provides an ideal diameter to reduce the rate of universe generation.
Mathematical analysis
Let us consider a steady laminar, heat transfer by mixed convection flow in front of a stagnation point of stretching and shrinking a wedge sheet. Let the x-axis be taken along the direction of the wedge and y-axis normal to it. The suction or injection of nanofluid is placed on the wedge surface, see Figure. 1. The temperature gradient in the y-direction is much larger than in the x-direction due to boundary layer behaviour, so only the velocity portion normal to the surface is relevant. The governing boundary layer equations of momentum, energy, and micro-rotation are under these conditions.
| Physical properties | Cu | Blood |
|---|---|---|
| CP (j/kg k) | 385 | 5000 |
| ? (kg/m3) | 8933 | 1060 |
| k (w/m k) | 400 | 0.719 |
| ßx10-5 (1/k) | 1.67 | 21 |
Table 1: Thermophysical properties of blood and cupper
p>Where u and v represent velocity components in the x and y directions, and μ_nf 〖,k〗^*_ represent relativity and vortex viscosities, respectively. The microrotation vector and the microinertia part material parameter are N and j, respectively. The acceleration due to gravity is g, and the fluid density is ρ _ f. The density of the nanoparticle is ρ_s, and the relativity density is ρ_nf, The temperatures of the fluid within the thermal boundary layer, the plate temperature, and the fluid temperature in the free stream are expressed by T,T_w and T_∞ respectively. The fluid's thermal conductivity is k _ f, the nanoparticle's thermal conductivity is k_s, and the relativity thermal conductivity is k_nfNumerical solution
The Gill and shooting methods (fourth order) were used with boundary conditions (9) with all variables.
| Case | S | suction | f'' (o) | w' (o) | - θ'(0) |
|---|---|---|---|---|---|
| parameter | |||||
| Stretching | 0.1 | 0.1188 | 0.1007 | 0.7263 | |
| 0.2 | 0.1231 | 0,1229 | 0.6762 | ||
| 0.5 | 0.0826 | 0.3276 | 0.4029 | ||
| Shrinking | 0.1 | 0.3425 | -0.0788 | 0.5270 | |
| 0.2 | 0.3394 | -0.1061 | 0.4790 | ||
| 0.5 | 0.2651 | -0.3768 | 0.3430 | ||
Table 1: Effect of nanoparticle.
| Case | S | suction | f'' (o) | w' (o) | - θ'(0) |
|---|---|---|---|---|---|
| parameter | |||||
| Stretching | 0 | 0.4702 | 0.0995 | 0.4824 | |
| 1 | -0.3517 | 0,1954 | 0.4202 | ||
| 2 | -02.0787 | 0.2971 | 0.1669 | ||
| Shrinking | 0 | 1.6728 | -0.1272 | 0.2879 | |
| 1 | 1.6638 | -0.0392 | 0.3840 | ||
| 2 | 0.8526 | 0.0571 | 0.4946 | ||
Table 2: Effect of suction parameter.
| Case | m | f'' (o) | w' (o) | - θ'(0) |
|---|---|---|---|---|
| Stretching | 0 | 0.2257 | 0.1478 | 1.1236 |
| 0.1 | 0.1927 | 0,1229 | 1.0248 | |
| 0.25 | 0.1874 | 0.1255 | 0.7377 | |
| Shrinking | 0 | 0.6402 | -0.0876 | 0.5898 |
| 0.1 | 0.6239 | -0.1061 | 0.5897 | |
| 0.25 | 0.6211 | -.01000 | 0.5334 |
Table 3: Effect of measure angle of wedge parameter.
Result and Discussion
The governing equations in new form, subject to the boundary conditions have been solved numerically by shooting technique method and (Range-Kutta) method for several values of Pr, m, s, k and M, while the non-dimensional constant A is fixed to be unity. The respective system of ordinary differential equations has been integrated. The effect of nanoparticle on nanofluids, which, passed over a shrinking and stretching wedge in the presence of suction [7-13].
We see the results appear from the Figure were 0 ≤φ≪0.1, suction parameter s=0,1,2 and magnetic field parameter M=0.1, pr =1, m=0,1,2and k=0,2,4.
Figures.(1-5) display the velocity profiles with various of parameters k and M respectively while the other parameters are fixed. Is observed the with boundary layer decreasing with, but increasing with s, m and M were increasing in to decelerate velocity, but the increasing in m, M to accelerate it [14]. Figure 6 display angular velocity decreasing with the increasing measure angle of wedge, but its inverse and increasing with increasing angle at point (Figures 7-10) display the velocity profiles with various of parameters, m, s, k and M respectively while the other parameters are fixed. Is observed the with boundary layer increasing with, but decreasing with s, m and M were increasing in accelerate to velocity, but the increasing in m, s, M to decelerate it [15].
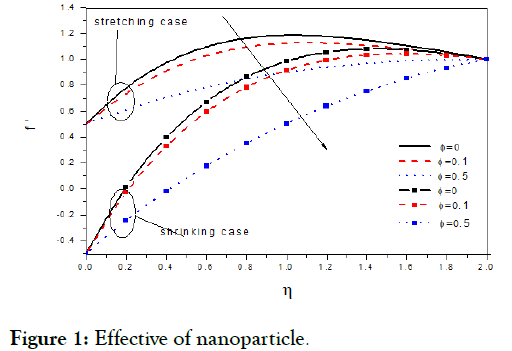
Figure 1: Effective of nanoparticle.
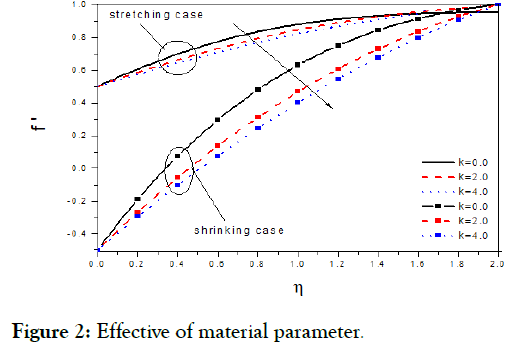
Figure 2: Effective of material parameter.
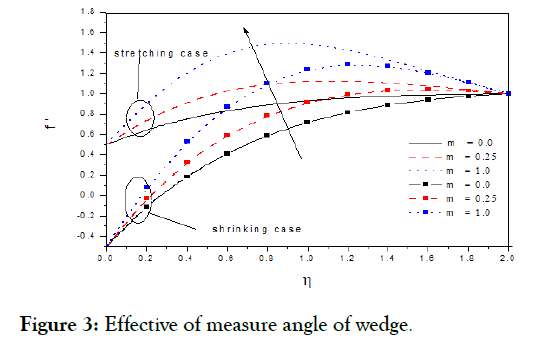
Figure 3: Effective of measure angle of wedge.
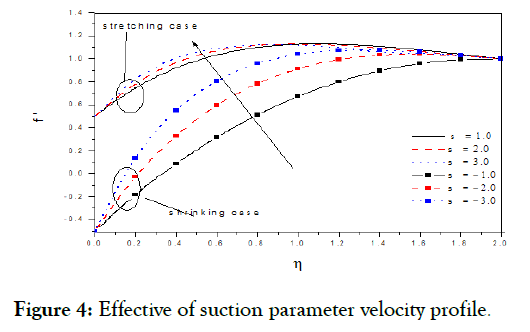
Figure 4: Effective of suction parameter velocity profile.
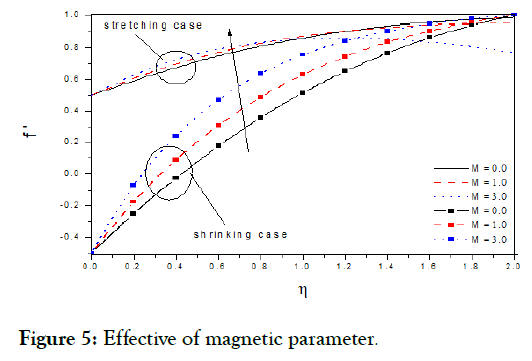
Figure 5: Effective of magnetic parameter.
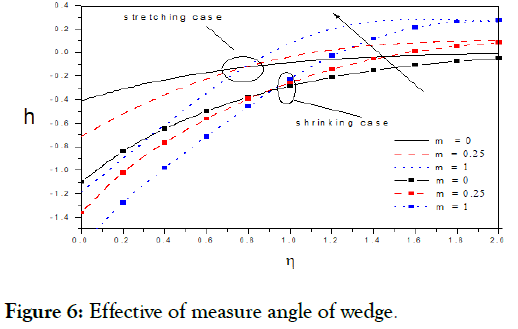
Figure 6: Effective of measure angle of wedge.
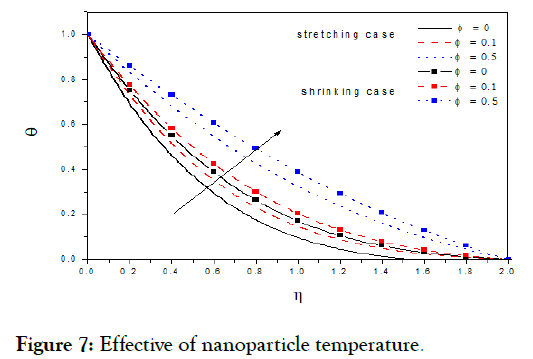
Figure 7: Effective of nanoparticle temperature.
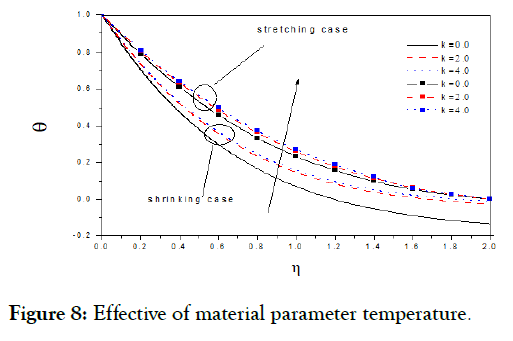
Figure 8: Effective of material parameter temperature.
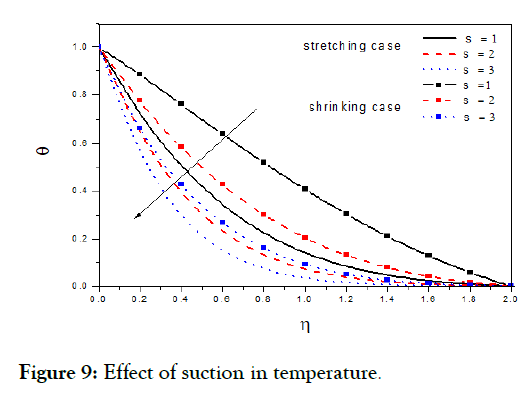
Figure 9: Effect of suction in temperature.
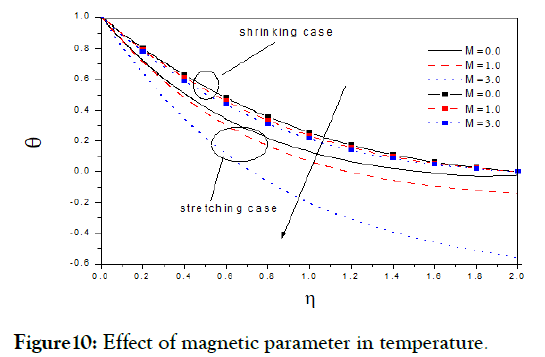
Figure10: Effect of magnetic parameter in temperature.
Conclusion
The effects of nanoparticles on non-Darcy mixed convective heat and heat transfer past a wedge with thermophoresis particle deposition effect were studied using numerical solutions. The final form of the mathematical model has several parameters involved. The problem can be generalized in several ways, the results are graphically presented, and the conclusion is drawn that these parameters have a major effect on the flow field and other physical quantities of interest. This research is expected to prove useful for studying the movement of oil or gas and water through the oil or gas reservoir sector, in the filtration and water purification systems, as well as in the migration of underground water.
REFERENCES
- Ahmadi G. Self-similar solution of incompressible micropolar boundary layer flow over a semi-infinite plate. Int J Engng Sci. 1976;14: 639-4.
- Yilbas BS. Laser short-pluse heating of gold-silver assembly entropy generation due to heat and electricity flows in electron subsystem,Numerical Heat Transfer. Int J Comp Method. 2006;49(9): 873-891.
- Ko TH. Numerical investigation of laminar forced convection and entropy generation in a helical coil with constant wall heat flux, Numerical Heat Transfer. J Comp Method. 2006;49(3): 257-278.
- Ejlali A, Hooman K. Entropy generation for forced convection in a Porous saturated circular tube with uniform wall temperature. Int Comm Heat Mass Trans. 2007;34: 408-419.
- Betchen LJ, Straatman AG. The development of a volume-averaged Entropy generation function for none-equilibrium heat transfer in high-conductivity porous foams, Numerical Heat Transfer. Int J Comp Method. 2008;53(5): 412-436.
- Iman Z. On the importance of thermal boundary conditions in Heat transfer and entropy generation for natural convection inside a porous enclosure. Int J Therm Sci.2008;47: 339-346.
- Yasin V, Hakan FO, Ioan P. Entropy generation due to natural convection in non-uniformly heated porous isosceles triangular enclosures at different positions. Int J Heat Mass Trans. 2009;52: 1193-1205.
- Alipanah M, Darbandi M, Hasannasab P, Hosseinizadeh SF. Entropy generation for compressible natural convection with high gradient temperature in a square cavity. Int Comm Heat Mass Trans. 2010;37: 1388-1395.
- John H, Lienhard V, Prakash NG, Syed MZ. Entropy Generation minimization of combined heat and mass transfer devices. Int J Therm Sci. 2010;49: 2057-2066.
- Basak T, Kaluri RS. Entropy generation minimization versus the Mixing due to natural convection in differentially and discretely heated square cavities Numerical Heat Transfer. Int J Comp Method. 2010;58(6): 475-504.
- Achintya M. Analysis of entropy generation due to natural convection in square enclosures with multiple discrete heat sources. Int Comm Heat Mass Trans. 2010;37: 867-872.
- Feng Yu, Clement Kleinstreuer. Nanofluid convective heat transfer in a parallel disk system. Int J Heat Mass Trans. 2010; 534619-4628.
- Anoop KB, Pawan KS, Sundararajan T, Sarit KD. Entropy generation due to flow and heat transfer in nanofluids. Int J Heat Mass Trans. 2010;53(21–22): 4757-47
- Jie Li, Clement K. Entropy generation analysis for nanofluid flow in microchannels. J Heat Trans. 2010;132: 122401-122408
- El-dawy HA. Mixed convection over Vertical Plate Embedded in a porous medium saturated with a nanofluid. J Nanofluids. 2014;3: 1-11.
Citation: Dawy HA, Gorla RSR (2021) The Flow of a Micropolar NanoFluid past a Stretched and shrinking over wedge surface with Absorption. J Nanomed Nanotechnol. 12: 561.
Copyright: © 2021 Dawy HA, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.