Indexed In
- Genamics JournalSeek
- JournalTOCs
- CiteFactor
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Publons
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
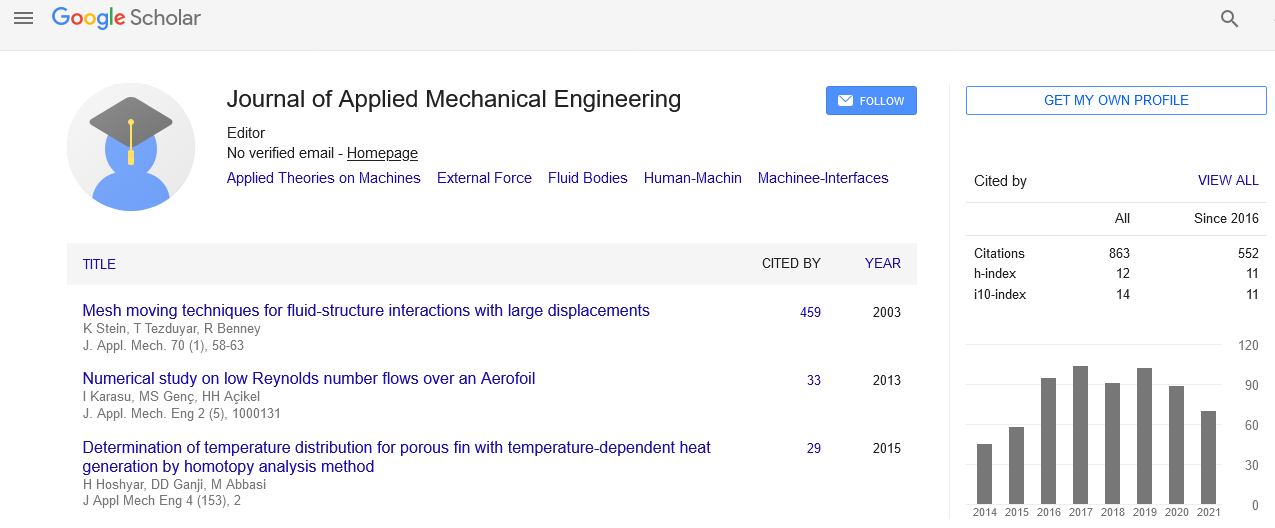
Research - (2019) Volume 8, Issue 1
The Comparison of Newtonian and Non-Newtonian Rheology Cases of the Solution of 2D Hydrodynamic Equations in the Boussinesq Approximation: A Mechanism of Upwelling Convective Flow Transporting Hydrocarbons
Andrey L Kharitonov1* and Sergei V Gavrilov22Schmidt Institute of Physics of the Earth of the RAS, Moscow, Bolshaya Gruzinskaya, Russia
Received: 29-Aug-2018 Published: 04-Jan-2019, DOI: 10.35248/2168-9873.19.8.314
Abstract
Thermo-mechanical model of the mantle wedge between the base of the overlying Scythian lithospheric plate and the upper surface of the Black Sea micro-plate subducting under the Scythian one with a velocity V at an angle β is obtained for the infinite Prandtl number fluid as a solution of non-dimensional 2D hydrodynamic equations in the Boussinesq approximation. For both Newtonian and non-Newtonian rheology cases 2D thermal viscous dissipationdriven convection mechanism in the mantle wedge above the Black Sea micro-plate subducting under the Crimea peninsula is modelled numerically. The effects of 410 km and 660 km phase transitions are taken into account. In the case of Newtonian rheology, the upwelling convective flow transporting heat to the Earth’s surface locates at far greater distance from the trench than they observed 2D heat flux anomaly. In the case of non-Newtonian rheology, the upwelling convective flow transporting heat to the Earth’s surface locates at twice greater distance from the trench than they observed 2D heat flux anomaly, the velocity in the convective vortices being over ∼10 m per year.
Keywords
2D hydrodynamic equations; Boussinesq approximation; Runge-Kutta method; Newtonian; Non-Newtonian rheology cases; Thermal convection; Subduction angle and velocity; Hydrocarbons transport
Introduction
Interaction of the lithospheric plates in the Crimea-Caucasus region leads to thrusting of the Black Sea micro-plate under the Crimea peninsula (under the Scythian plate) [1]. As a consequence, the seismic focal plane is formed along which the Crimea ascends as the result of seismic jerks. The velocities of vertical uplift of the Crimea mountains and sinking of the near-Crimean area of the Black Sea micro-plate equal to ∼4 mm per year and ∼10 mm per year respectively. Mountainous Crimea is a folded fault region being a part of the Alps-Himalaya- Indonesia belt [2-5]. The velocity of subduction of the Black Sea microplate under the Crimea peninsula remains unknown. According to [3-5] two types of dissipation-driven small-scale thermal convection in the mantle wedge are possible, viz. 3D finger-like convective jets, raising to volcanic chain, and 2D transversal Karig vortices, aligned perpendicularly to subduction. These two types of convection are shown to be spatially separated due to the pressure and temperature dependence of mantle effective viscosity, the Karig vortices, if any of them formed, being located behind the volcanic arc [6]. Despite the firmly established localization of both seismic focal plane and the deepsea trench parallel to the southern shore of Crimea there are no definite conclusions concerning the velocity of subduction of the Black Sea micro-plate. It is not completely clear if volcanism played a substantial role in forming Mountainous Crimea or the mountains are of a purely thrust-and-fold origin. Nimelulayeva [1] indicates the contradictory statements on the Crimean volcanism to have been published, however in Figure 1 in Nimelulayeva [1] the volcanic eruption in the Mountainous Crimea is depicted. The abovementioned picture is reproduced here in Figure 1 with the convective vortices drawn additionally. It is worth assuming the two heat flux anomaly maxima observed in the south of the Crimea peninsula [1,7] owe their origin to respectively 3D and 2D upward convective heat transfer from the mantle wedge to the Earth’s surface (Figure 1). The latter 2D maximum located in the rear of the Mountainous Crimea is much greater as compared to the former 3D maximum located in the Mountainous Crimea. The 2D heat flux anomaly maximum obviously is associated with the 2D upward convective flow in the mantle wedge. Numerical modelling of 2D mantle wedge thermal convection occurring in the form of the Karig vortices and presumably transporting heat to the Earth’s surface in the rear of the Mountainous Crimea allows to judge about the mean velocity of subduction of the Black Sea micro-plate under the Crimea peninsula as well as about the rheological mantle parameters. Horizontal extent of the 2D heat flux anomaly in the rear of the Mountainous Crimea is shown to correspond to the mean subduction velocity ∼45 mm per year for the observed subduction angle ~15°. Numerical convection models accounting for the effects of phase transitions as well as the pressure, temperature and viscous stresses viscosity dependence fit in well with the heat flux observation data in the case of non-Newtonian mantle rheology at the mantle wedge water concentration ~3 × 10-1 weight%.
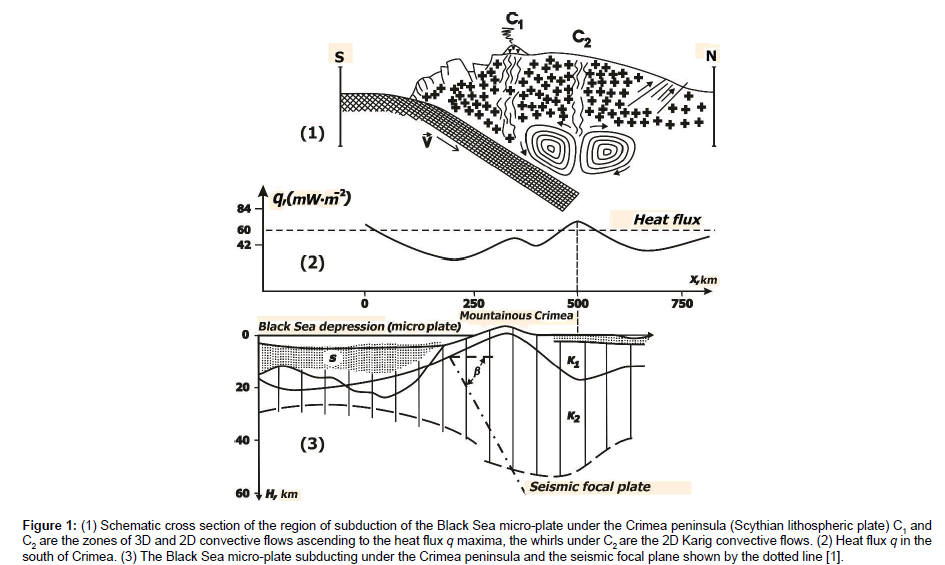
Figure 1: (1) Schematic cross section of the region of subduction of the Black Sea micro-plate under the Crimea peninsula (Scythian lithospheric plate) C1 and C2 are the zones of 3D and 2D convective flows ascending to the heat flux q maxima, the whirls under C2 are the 2D Karig convective flows. (2) Heat flux q in the south of Crimea. (3) The Black Sea micro-plate subducting under the Crimea peninsula and the seismic focal plane shown by the dotted line [1].
Materials and Methods
Thermo-mechanical model of the mantle wedge between the base of the overlying Scythian lithospheric plate and the upper surface of the Black Sea micro-plate subducting under the Scythian one with a velocity V at an angle β is obtained for the infinite Prandtl number fluid as a solution of non-dimensional 2D hydrodynamic equations in the Boussinesq approximation:
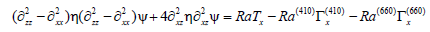 (1)
(1)
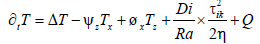 (2)
(2)
For the stream function ψ and temperature T. Here η is non-dimensional dynamic viscosity, ∂ and indices denote partial derivatives with respect to coordinates x (horizontal), z (vertical) and time t, Δ is the Laplace operator, Г(410) and Г(660) are volume ratios of the heavy phase at the 410 km and 660 km phase boundaries, the velocity components Vx and Vz are expressed through ψ as:
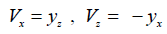 (3)
(3)
and non-dimensional Rayleigh number Ra, phase Ra (410), Ra (660) and dissipative number Di are defined as follows
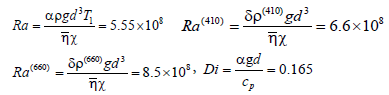 (4)
(4)
Where a =3.10-5 K-1 is thermal expansion coefficient, ρ=3.3 g × cm-3 is
the density, g is gravity acceleration, cp=1.2103 J × kg-1 × K-1 is specific
heat capacity at constant pressure, T1=1950 K is the temperature at
the upper mantle transient zone (MTZ) base at 660 km depth with the
latter being the lower boundary of the modeled domain, Q=6.25.10-4 μ
× W × m-3 is the volumetric radiogenic heat relies power in the crust,
τik is the viscous stress tensor, d=660 km is the vertical dimension of
the modeled domain, 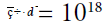 Pa × s is the viscosity scaling factor, χ= 10-2 cm2 × s-1 is thermal diffusivity,δρ(410)=0.07ρ andδρ(660)= 0.09ρ are
the density changes at phase transitions at 410 km и 660 km depths. In
(1), (2) the scaling factors for time t, stresses τik and stream-function Ψ are
Pa × s is the viscosity scaling factor, χ= 10-2 cm2 × s-1 is thermal diffusivity,δρ(410)=0.07ρ andδρ(660)= 0.09ρ are
the density changes at phase transitions at 410 km и 660 km depths. In
(1), (2) the scaling factors for time t, stresses τik and stream-function Ψ are 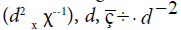 and χ respectively. Assuming rheology be
linear for the diffusion creep deformation mechanism dominating in
the mantle at depths over ~200 km [8], we accept the temperature- and
lithostatic pressure p dependent viscosity as 9. Zharkov [9]
and χ respectively. Assuming rheology be
linear for the diffusion creep deformation mechanism dominating in
the mantle at depths over ~200 km [8], we accept the temperature- and
lithostatic pressure p dependent viscosity as 9. Zharkov [9]
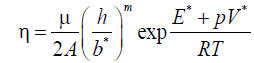 (5)
(5)
Where for “wet” olivine A=5.3 × 1015 s-1, m=2.5, the grain size h=10-1 -10 mm, Burgers vector is b*=5 × 10-8 cm [10], activation energy is E*=240 kJ × mol-1, activation volume V*=5 × 103 mm3 × mol-1 is activation volume, = 300 GPa is normalizing factor of the shear modulus, R is universal gas constant. Under grain size h=1.6 mm, ç = 1018 Pa × s and abovementioned values of constants non-dimensional viscosity also denoted η is:
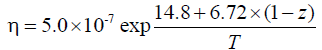 (6)
(6)
Where T is non-dimensional temperature, non-dimensional z normalized by d is pointing upwards from the MTZ base and x is pointing against subduction along the MTZ base. The aspect ratio of the model domain is 1:3.7 thus the subduction angle being β=15° if subduction is assumed to take place along the model domain diagonal. Non-dimensional subduction velocity V=45 mm.yr-1 normalized by (d-1xc) equals V=0.938 × 103, i.e. non-dimensional velocity components of subducting Black Sea micro-plate are Vx= -0.898 × 103 and Vz=-0.268 × 103.
To check as to how the estimate of velocity of subduction of the Black Sea micro-plate is sensitive to the accepted linear rheological law here, we make extra computations for non-Newtonian rheology, in which case the viscosity formulae (5)-(6) are rewritten as
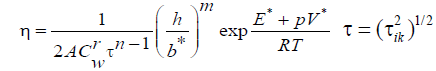 (7)
(7)
Where according to Trubutsyn [11] for “wet” olivine n=3, r=1.2, m=0, E*=480 kJ.mol-1, V*=11 × 103 mm3.mol-1, A=102 с-1 × (MPa)-n, Cw>10-3 for “wet” olivine is the weight water concentration (in%%). It should be noted the constants in equation 7 vary considerably in the papers referred to by Trubutsyn [11] and heretofore we gave averaged values of constants.
At Cw=10-3 on accounting for
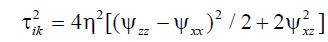 (8)
(8)
non-dimensional viscosity is
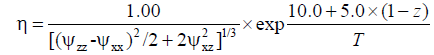 (9)
(9)
Following Trubutsyn [12] we assume the phase functions Г(l) as
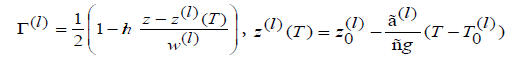 (10)
(10)
Where the signs are changed as z-axis is pointing upwards, z(l)(T) is the depth of the l-th phase transition (l=410, 660), z0(l) and T0(l) are the averaged depth and temperature of the l-th phase transition, (410)=3 MPa×K-1 and γ(660)=-3 MPa×K-1 are the slopes of the phase equilibrium curves, w(l) is the characteristic thickness of the l-th phase transition, T0(410)=1800o K, T0(660)=1950o K are the mean phase transition temperatures. The heats of phase transitions are neglected in equation 2 as insignificant in the case of developed convection as by Trubutsyn [12]. From equation 10 it follows:
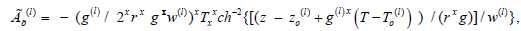 (11)
(11)
Where from it is clear the phase transition with 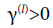 facilitates
convection (at l=410), while the phase transition with γ(l)<0 hinders
convection (at l=660). In non-dimensional form z0(410)=0.38, z0(660)=0,
w(l)=0.05, γ(410)=2.5×109, T0(410)=0.92, T0(660)=1, and in (1):
facilitates
convection (at l=410), while the phase transition with γ(l)<0 hinders
convection (at l=660). In non-dimensional form z0(410)=0.38, z0(660)=0,
w(l)=0.05, γ(410)=2.5×109, T0(410)=0.92, T0(660)=1, and in (1):
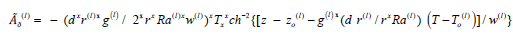 (12)
(12)
Equation 1 and equation 2 are solved for the isothermal horizontal and insolated vertical boundaries regarded no-slip impenetrable ones except for the “windows” for in- and outgoing subducting plate, where the plate velocity is specified. Vertical boundary distant from subduction zone is assumed penetrable at right angle, the latter boundary condition appears not too imposing in the case of very flat subduction. Q in equation 2 is non-zero in the continental and oceanic crust 40 and 7 km thick. Initial vertical boundaries temperature is calculated for the half-space cooling model for 109 yr and 108 yr for Scythian (continental) and Black Sea (oceanic) plates respectively. It is convenient to express dimensionless 2ik in equation 2 through the stream-function Ψ as in equation 8:
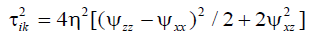
Results and Discussion
Assuming the second (more remote from the trench) heat flux q maximum in Figure 1 appears above the convective flow, ascending to C2 point in Figure 1, and the convection cell dimension is equal to the two adjacent q minima separation (i.e. the q minima are located above the descending convective flows) we can estimate the convection cell dimension as ~250 km. To preliminarily access the mean velocity of subduction of the Black Sea micro-plate the coordinate x dependence of the growth rate γ1(x) of transversal convective rolls for the constant viscosity fluid model can be allowed for. In such the model the average temperature and pressure viscosity dependence is accounted for in an averaged manner, the factor describing the temperature- and pressure viscosity dependence being equal to its mean value [3].
Analytical formulae by Gavrilov [3] yield γ1(x) shown in Figure 2 for the subduction angle β=15° convection cell dimension ~250 km and subduction velocities V given in Figure 2 in mm per year.
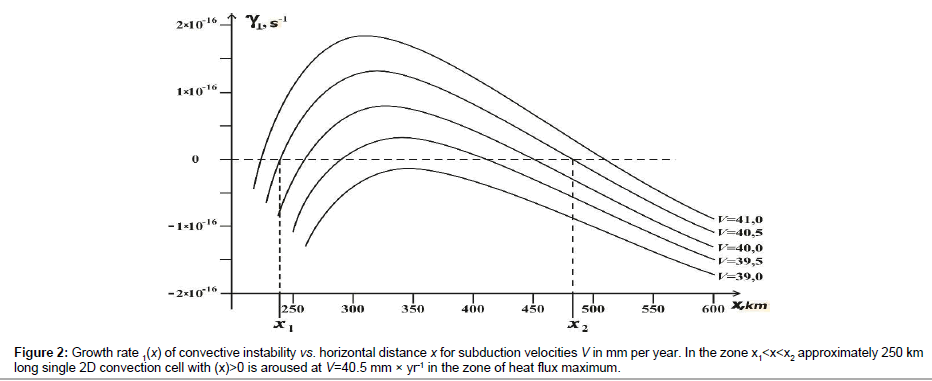
Figure 2: Growth rate 1(x) of convective instability vs. horizontal distance x for subduction velocities V in mm per year. In the zone x1<x<x2 approximately 250 km long single 2D convection cell with (x)>0 is aroused at V=40.5 mm × yr-1 in the zone of heat flux maximum.
It should be noted the growth rates γ1(x) are viscosity independent as convection is driven by viscous heat release (which is directly proportional to viscosity), while, on the other hand, the greater is the viscosity the more difficult is to arouse the convection. Figure 2 clearly demonstrates the convective zone with γ1(x)>0 amounts to (x2 – x1)=250 km (i.e. the single convective cell of ~250 size is actually aroused) at V=40.5 mm per year, the latter value being a preliminary estimate of the mean subduction velocity. The γ1(x) maximum is ~320 km distant from the trench which is very close to the distance from the trench to the observed 2D heat flux anomaly (~400 km, see Figure 1).
To compute more accurate consistent model of small-scale convection in the mantle wedge between the overriding Scythian plate and subducting Black Sea micro-plate it is necessary from the computational point of view first to specify in equation (1)-(2) vanishing non-dimensional numbers Ra→0, Di=0, i.e. to ignore convection and viscous dissipation. This approach is applied as convection with Ra and Di (4) passes through very vigorous stages, and the time steps in integrating equation (1)-(2) become too small thus making it difficult to model the thermal structure of the plates. Solving equation (1)-(2) by the finite element method in space on the grid 104×104 and the 3-rd order Runge-Kutta method in time one obtains for Ra→0, Di=0 and V=45 mm a year non-dimensional quasi steady-state Ψ and T shown in Figure 3, where the streamlines are depicted with the step 0.25 and the isotherms with an interval 0.05. Subducting plate was considered rigid, while the viscosity at the zone of plate’s friction (at temperatures below 1200 K) was reduced by 2 orders of magnitude as compared to equation 5. The latter viscosity reduction at the plates contact zone accounts for lubrication effected by deposits partially entrained by the subducting plate.
Such a lubrication prevents the overriding Scythian plate from gluing to the subducting one [5]. It is worth noting the isotherm T=0.15 in Figures 3a and 3c approximately corresponding to the Earth’s surface is depressed at subduction zone by ~7 km which is of the order of a typical trench depth. Figure 3 shows the results of computation for formulae equation (7)-(9) for non-Newtonian rheology case for the water content Cw=10-3 weight%% (Figures 3a and 3b) and Cw=3 × 10-1 weight%% (Figures 3c and 3d). The velocity V=45 mm per year is chosen as resulting in the best convective zone size fitting in with the observed heat flux (positive and negative) anomaly size at the point C2 in Figure 1, i.e. in the rear of the Mountainous Crimea. The Black Sea micro-plate subducting with a given velocity V is considered rigid and is shown in Figures 3b and 3d by the equidistant diagonal streamlines. The induced mantle wedge flow above the subducting plate is seen to occur in the form of a single vortex at Cw=10-3 weight%% (Figure 3b) and in the form of the 2 vortices (located one above another) at Cw=3 × 10-1 weight%% (Figure 3d), the latter 2 vortices being considerably compressed in the vertical direction and the upper one (with Ψ >0) revolves clockwise while the lower one (with Ψ< 0) revolves counterclockwise (Figures 3b and 3d). Micro-whirls ~102 km great are formed between the counterflows inside the upper induced flow obviously due to the tangential discontinuity instability (Kelvin-Helmholtz instability).
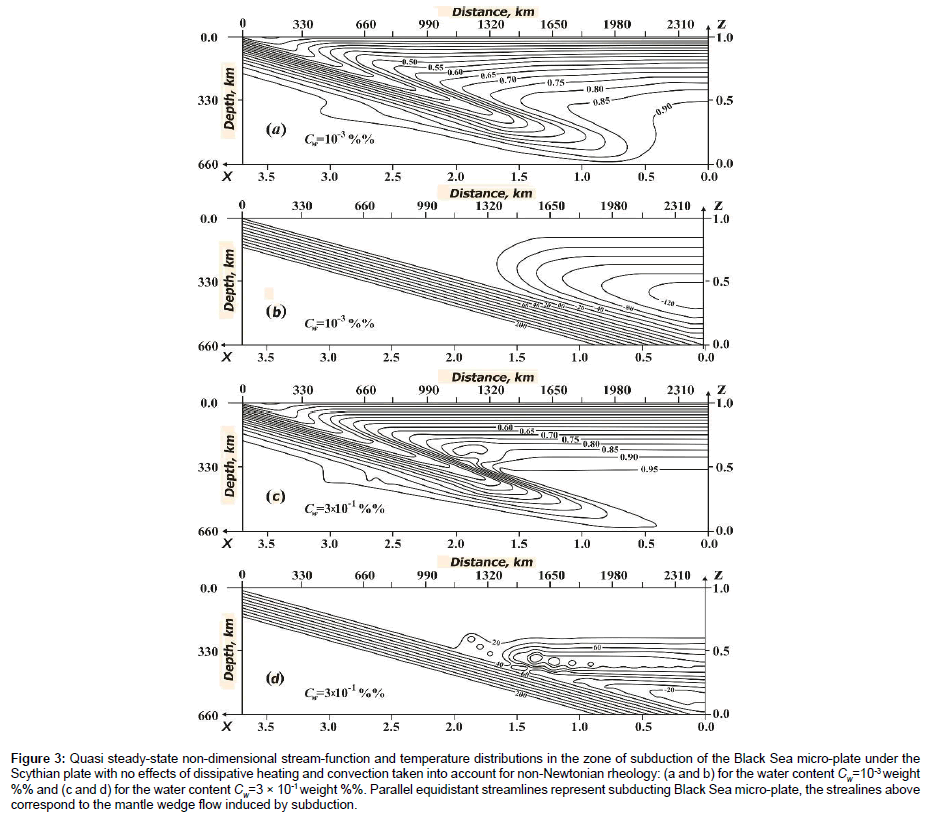
Figure 3: Quasi steady-state non-dimensional stream-function and temperature distributions in the zone of subduction of the Black Sea micro-plate under the Scythian plate with no effects of dissipative heating and convection taken into account for non-Newtonian rheology: (a and b) for the water content Cw=10-3 weight %% and (c and d) for the water content Cw=3 × 10-1 weight %%. Parallel equidistant streamlines represent subducting Black Sea micro-plate, the strealines above correspond to the mantle wedge flow induced by subduction.
Assuming Ra=5.55 × 108 and Di=0.165, i.e. switching dissipation and convection on, and taking into account the effects of phase transitions, from equation 1– equation 2 the convection is found not to arouse in the non-Newtonian rheology case at Cw= 10-3 weight%%. At Cw=3 × 10-1 weight%% the 2 induced mantle flows in the mantle wedge are destroyed during the time interval ~ 0.6 × 10-6 (in dimensional form ~ 0.1 Myr) by the convective vortices shown in Figure 4 with the streamlines depicted with the interval 4 × 104.
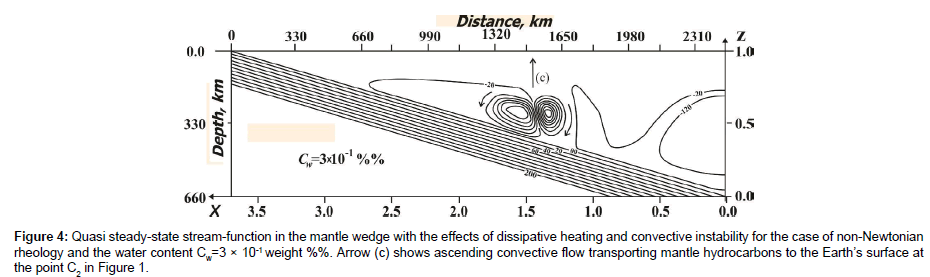
Figure 4: Quasi steady-state stream-function in the mantle wedge with the effects of dissipative heating and convective instability for the case of non-Newtonian rheology and the water content Cw=3 × 10-1 weight %%. Arrow (c) shows ascending convective flow transporting mantle hydrocarbons to the Earth’s surface at the point C2 in Figure 1.
These convective vortices are seen actually to correspond to a single convection cell aroused at subduction velocity V=45 mm per year. The latter convection cell dimension is of the order of ~300 km, i.e. is very close to the observed minima q separation under the C2 point in Figure 1.
Thus the for the non-Newtonian mantle wedge rheology case with the viscosity reduced by 3 orders of magnitude as compared to equation 7–equation 9 the computation shows the convection in the mantle wedge to occur at Cw=3×10-1 weight%% in the form of two micro vortices at V=45 mm per year. Convection of this type can provide abnormal 2D heat flux q observed in the rear of the Mountainous Crimea. Alternatively, the water content can be not that greatly increased but the constant A in equation 7 might have been an order (or so) of magnitude greater. Considerable velocity in convective vortices in Figure 4 is due to the local viscous stresses increase resulting in the drop in viscosity in convective zone. It is worth noting the mantle wedge dissipation-driven convection in the form of transversal rolls as in Figure 4 is characteristic of very small subduction angles the convection of this type being absent already at subduction angle β=30° [13]. At the subduction angle under consideration here, β=15°, the convective transversal rolls do not appear at V<4 cm × yr-1. Arrow (c) above the boundaries of the oppositely revolving convective vortices in Figure 4 indicate possible direction of transport of non-organic mantle hydrocarbons to the Earth’s surface. Computations for Newtonian mantle rheology with the viscosity equation 5-equation 6 shows the transversal rolls to be aroused at far greater distance from the trench than the observed 2D heat flux anomaly. Thus, the model constructed here favors the non-Newtonian mantle wedge rheology as better fitting in with the observed heat flux anomaly localization. It should be noted that numerous thermo-mechanical mantle models in the zones of subduction (see, e.g. [4,5] and the vast number of references there) showed convection in the form of transversal rolls never to occurred as the models with extremely small subduction angle and sufficiently great subduction velocity were not investigated.
Conclusion
The size of the cell of 2D mantle wedge dissipation-driven convection in the case of the realistic non-Newtonian rheology equals ~300 km at the subduction velocity 45 mm×yr-1, in which case a single convection cell is aroused. This explains the formation and horizontal extent of the only 2D heat flux anomaly observed in the rear of the Mountainous Crimea. The water content enough for the 2D convection be aroused is ~3×10-1 weight%%, or, alternatively, it is, say, ~3 × 10-2 weight%%, but the constant A in the rheological law is an or[der of magnitude greater than generally accepted. The non-Newtonian model convection cell locates twice further from the trench than the 2D heat flux anomaly is observed, this discrepancy being even greater in the case of Newtonian rheology. However linear onset of convection model shows the position of 2D convection cell to nearly coincide with the observed 2D heat flux anomaly for constant viscosity fluid model for subduction velocity 40 mm per year. The velocity in convective vortices in the non-Newtonian rheology case is ~10 m per year which may be enough to provide upward transport of mantle wedge hydrocarbons to the Earth’s surface.
Acknowledgements
The authors would like to express sincere thanks to Dr. Joseph Abraham for his help in publishing the paper.
REFERENCES
- Nimelulayeva G. Peculiarities of the influence of natural factors and their bearing on formation of the land-slide processes in Crimea. Culture of the Near Black Sea People. 2006;83:110-113.
- Yudin VV. Crimea geology on the geodynamical basis, Simpheropol. 2001;2:1.
- Gavrilov SV. Investigation of the mechanism of island arc formation mechanism and the back-arc lithosphere spreading of the lithosphere. Geophysical Researches. 2014;5:35-43.
- Gerya TV, Connolly JAD, Yuen DA, Gorczyk W, Capel P. Seismic implications of mantle wedge plumes. Phys Earth Planet Inter. 2006;156:59-74.
- Gerya T. Future directions in subduction modeling. J Geodyn. 2011;52:344-378.
- Gavrilov SV, Kharitonov AL. Subduction velocity of the Russian plate under the Siberian one at Paleozoic: A constraint based on the mantle wedge convection model and the oil and gasbearing zones distribution in Western Siberia. Modern Science. 2016;16:155-160.
- Smirnov-Ya B. The map of heat flux at the territory of the USSR and adjacent regions. 1980.
- Billen M, Hirth G. Newtonian versus non-Newtonian upper mantle viscosity: Implications for subduction initiation. Geophys Res Lett. 2005;p:32.
- Zharkov VN. Physics of the Earth’s Interiors. Moscow, Science and Education. 2012.
- Zharkov VN. Geophysical researches of the planets and satellites. Moscow, Joint Institute of Physics of the Earth RAS. 2013;p:102.
- Trubutsyn VP. Rheology of the mantle and tectonics of oceanic lithosphere plates. Izv Phys Solid Earth. 2012;6:3-22.
- Trubutsyn VP. Trubitsyn AP Numerical model of formation of the set of lithospheric plates and their penetration through the 660 km boundary. Izv Phys Solid Earth. 2014;6:138-147.
- Gavrilov SV, Abbott DH. Thermo-mechanical model of heat and masstransfer in the vicinity of subduction zone. Izv Phys Solid Earth. 1999;35:967-976.
Citation: Kharitonov AL, Gavrilov SV (2019) The Comparison of Newtonian and Non-Newtonian Rheology Cases of the Solution of 2D Hydrodynamic Equations in the Boussinesq Approximation: A Mechanism of Upwelling Convective Flow Transporting Hydrocarbons. J Appl Mech Eng 7: 314. doi: 10.35248/2168-9873.19.8.314
Copyright: © 2019 Kharitonov AL, et al. This is an open access article distributed under the term of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.