International Journal of Swarm Intelligence and Evolutionary Computation

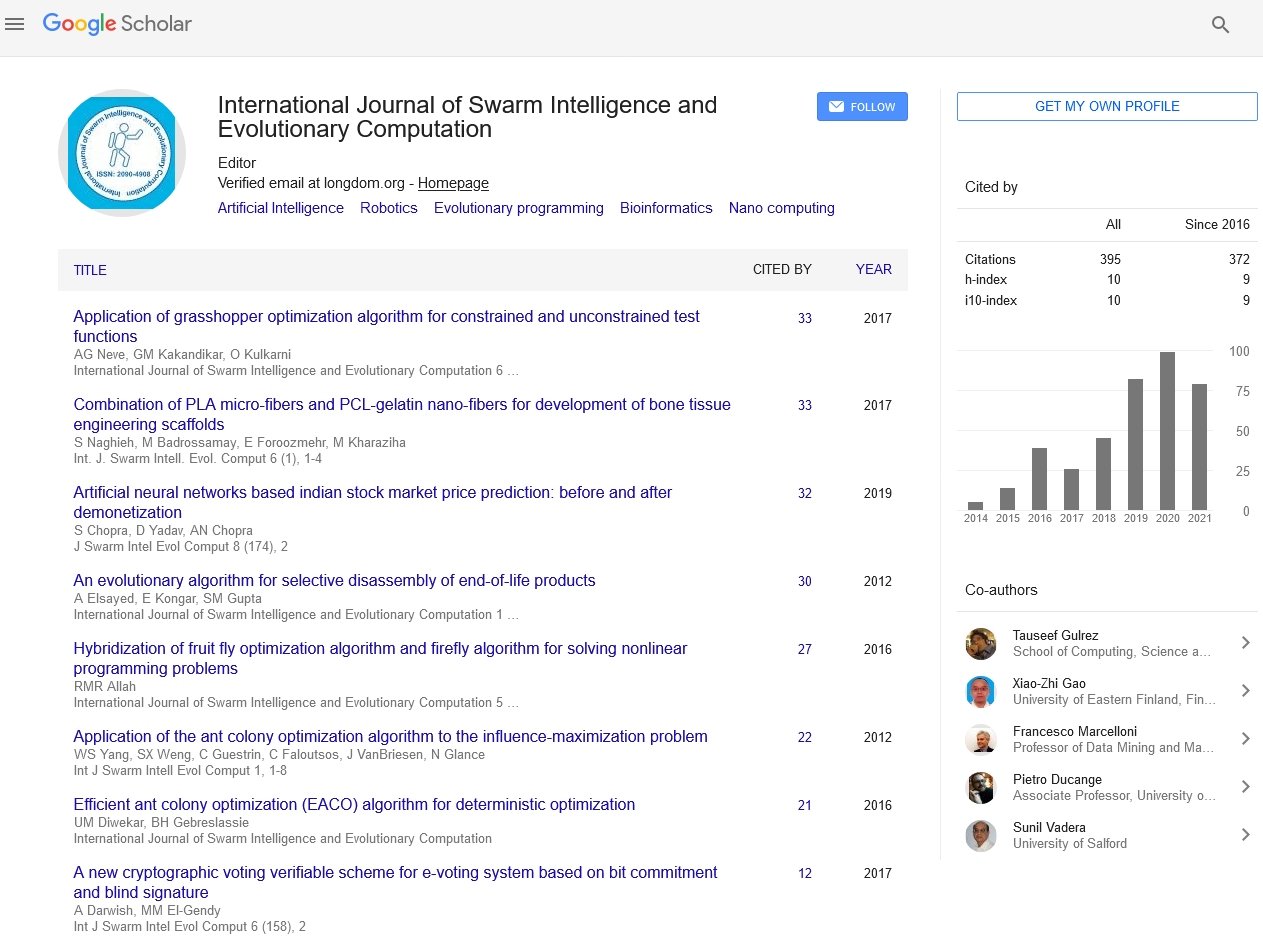
Significance of Meta-heuristics in Swarm Intelligence

Feign Chein^* Department of Communication Sciences, University of Texas, Austin, USA
^*Correspondence: Feign Chein, Department of Communication Sciences, University of Texas, Austin, USA, Email:

Received: 01-Sep-2022, Manuscript No. SIEC-22-18842; Editor assigned: 05-Sep-2022, Pre QC No. SIEC-22-18842 (PQ); Reviewed: 19-Sep-2022, QC No. SIEC-22-18842; Revised: 26-Sep-2022, Manuscript No. SIEC-22-18842 (R); Published: 03-Oct-2022, DOI: 10.35248/2090-4908.22.11.278

Description

A meta-heuristic algorithm is a search procedure designed to find a good solution to a complex and difficult to solve optimization problem. In this world of limited resources, it is critical to find a near-optimal solution based on imperfect or incomplete information. One of the most notable achievements in operations research over the last two decades has been the development of meta-heuristics for solving such optimization problems.

Meta-heuristic optimization is the application of meta-heuristic algorithms to optimization problems. Optimization is used in almost every aspect of life, from engineering design to economics, and from vacation planning to Internet routing. Because money, resources, and time are always limited, making the best use of these resources is critical. The majority of realworld optimizations are highly nonlinear and multimodal, with a variety of complex constraints. Different goals are frequently at odds. Even for a single goal, optimal solutions may not exist at all times. Finding an optimal or even sub-optimal solution is not an easy task in general. This article will cover the fundamentals of meta-heuristic optimization as well as some well-known metaheuristic algorithms.

There are challenges that require attention in order to develop better solutions than the existing traditional approaches. Authors describe various meta-heuristic algorithms that are applicable to a wide range of non-linear non-convex optimization problems. Specific NP-hard problems are impossible to solve in combinatorial optimization. As a result, meta-heuristics can frequently find good solutions while requiring less computational effort than optimization algorithms, iterative methods, and simple greedy heuristics. There are numerous problems that are impractical to solve using an optimization algorithm to achieve global optimality. When there are stochastic random variables in the objective or constraints, for example, an optimization problem becomes complex. As a result, solving large-scale stochastic programmes using stochastic programming or robust optimization techniques is difficult.

Meta-heuristics can be useful in a variety of domains. Many optimization problems are, in essence, multi-objective functions with non-linear constraints. For example, most engineering optimization problems are highly non-linear and necessitate solutions to multi-objective problems. Artificial intelligence and machine learning problems, on the other hand, rely heavily on large datasets, and it is difficult to formulate the optimization problem to solve for optimality. As a result, meta-heuristics are important in solving practical problems that are difficult to solve using traditional optimization methods.

Conclusion

Nature-inspired vs non-nature-inspired meta-heuristic algorithms, population-based vs. single point search, dynamic vs static objective functions, one vs various neighborhood structures, memory usage vs memory-less methods are examples of meta-heuristic algorithms. This article is not intended to compare search and optimization techniques. Nonetheless, it is critical to question whether traditional search methods meet the requirements for robustness. Meta-heuristics are appropriate for both solution space exploitation and exploration.

Intensification and diversification, or exploitation and exploration, are two major components of any meta-heuristic algorithm. Diversification means generating diverse solutions in order to explore the search space on a global scale, whereas intensification means focusing the search in a local region where a current good solution is found. To improve the rate of algorithm convergence, a good balance between intensification and diversification should be found during the selection of the best solutions. The best solutions are chosen to ensure that they will converge to the optimum, whereas diversification via randomization allows the search to espace from local optima while also increasing the diversity of solutions. Usually, a good combination of these two major components will ensure that global optimality is achievable.