Indexed In
- Open J Gate
- Genamics JournalSeek
- Academic Keys
- JournalTOCs
- ResearchBible
- Electronic Journals Library
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Proquest Summons
- SWB online catalog
- Virtual Library of Biology (vifabio)
- Publons
- MIAR
- Euro Pub
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Research Article - (2023) Volume 14, Issue 6
Secure Haplotype Imputation Employing Local Differential Privacy
Marc Harary1,2,3*2Department of Biomedical and Genomic, Harvard University, Massachusetts, United States of America
3Department of Computational Biology, Dana-Farber Cancer Institute, Boston, United States of America
Received: 06-Oct-2023, Manuscript No. JPP-23-23412; Editor assigned: 09-Oct-2023, Pre QC No. JPP-23-23412 (PQ); Reviewed: 23-Oct-2023, QC No. JPP-23-23412; Revised: 30-Oct-2023, Manuscript No. JPP-23-23412 (R); Published: 06-Nov-2023, DOI: 10.35248/2153-0645.23.14.076
Abstract
Recent literature has highlighted the security risks to human research subjects forfeiting sensitive genomic data to public reference panels. Such breaches to subject privacy may occur even in largescale biomedical analyses like genotype imputation, a preliminary stage of many clinical studies. To this end, we introduce Secure Haplotype Imputation Employing Local Differential Privacy (SHIELD). As a server-side pipeline, it combines the differentially private randomized response mechanism and the standard forward-backward algorithm to compute a Markov random field over incomplete genomic datasets submitted by client researchers. Critically, we show that SHIELD achieves modern imputation accuracy well within typical privacy budgets, providing mathematically provable privacy guarantees to reference panel donors without sacrificing client utility. We conclude that developing practicable, differentially private workflows individual methods in several domains of genomic research.
Keywords
Secure Haplotype Imputation Employing Local Differential Privacy (SHIELD) program; Genomic privacy risks; Imputation algorithms in genetics; Haplotype reference panel; Genomic medicine
Introduction
Just as the additional of novel biomedical technologies has grown with the rapid development of genomic medicine over the past decade, so too have the privacy risks for human subjects volunteering sensitive data to academic or corporate researchers. Ever larger datasets like the UK Bio bank (UKB), all of us research program, Haplotype reference consortium, and 1,000 genomes project (1KG) render genomic and in-depth Protected Health Information (PHI) on hundreds of thousands of participants widely available to approved institutions [1-4]. The rising popularity of consumer sequencing services like 23 and the opportunity, Ancestry DNA, and family tree DNA have resulted in the corporate data mining of the results from millions of test kits across a number of populations [5-7]. Likewise, cloud-based platforms like Terra, Google’s Cloud Life Sciences API, and IntelliSpace Genomics tremendously facilitate the maintenance, cleaning, and processing of large datasets in standardized and reproducible workflows, further accelerating the proliferation of private data collected for biomedical studies [8-10].
In order to protect patient privacy, protocols like those stipulated by the Health Insurance Portability and Accountability Act (HIPPA) of 1996 have been enacted to restrict the distribution of Personally Identifiable (PID) information and PHI [11]. However, as part of a growing literature on privacy concerns in genomic research, it has also been documented that coordinated attacks on the part of cryptographic adversaries are capable of compromising the privacy of research subjects that donate to public datasets even when such procedures are followed and PID is made inaccessible [12-15]. Reconstruction attacks that divulge the contents of an otherwise private database are in fact possible in nearly any scenario in which researchers are able to request statistical estimates of sample parameters [16]. In brief, such attacks are made possible by the fact that a malefactor may make a carefully coordinated series of queries to reconstruct the contents of a target dataset with arbitrary accuracy. Specifically, in a genomic context, law enforcement authorities have exploited consumer genomic databases to identify distant familial relatives of suspects in what has been shown to be a highly effective statistical attack [17]. Other researchers have demonstrated that short tandem repeats on the Y-chromosome of targets can be cross-referenced with publicly available genealogy data to, in combination with other demographic information, reliably identify individuals [18]. Such risks occur even when targets exist in the midst of massive datasets; forensic techniques have been shown to detect the presence of individuals in highly complex DNA mixtures in which less than 0.1% of the total genomic material is contributed by the target [15].
Among the many components of typical genomic workflows, imputation constitutes one of the most common applications of public data in which repeated queries are made to a single database, thereby enabling reconstruction attacks and other privacy breaches. Because whole-genome sequencing remains prohibitively expensive for existing high-throughput technology, array-based genotyping platforms provide a more efficient method of collecting data for large-scale studies of human disease. This comes at the expense of the statistical power of Genome-Wide Association Studies (GWAS) that intend to fine-map causal variants or facilitate meta-analyses, necessitating a preliminary stage in which an imputation algorithm infers the genotype for a given target genome at loci that have not been directly assayed, essentially expanding the dimensionality of the original dataset [19-31]. Employing a reference panel of donated haplotypes sequenced via higherquality technology and at a far denser set of variants, imputation algorithms like MaCH, Minimac, BEAGLE, PLINK, fastPHASE, and IMPUTE have been demonstrated to reliably augment both the coverage and statistical power of GWAS and hence become an essential component of many clinical studies [19-28,32]. An urgent challenge is therefore to develop a suite of imputation algorithms that can simultaneously facilitate high-utility, statistically reliable GWAS while protecting the privacy of contributors to reference haplotype panels [12,33,34].
One solution to security concerns in imputation and other stages of genomic research is the technique of differential privacy, which has rapidly become the “gold-standard” for statistical queries by being able to provide both robust privacy guarantees for participants in studies and meaningful results for researchers in commercial and scientific settings [35-37]. At the crux of the technique is a rigorous mathematical formalization of privacy that quantifies the extent to which adding pseudorandom noise to the results of computations can protect the anonymity of members of a database [38].
The following work introduces Secure Haplotype Imputation Employing Local Differential privacy (SHIELD), a program that employs the Li-Stephens model of genetic recombination to impute missing haplotype variants in target genomes while incorporating differential privacy techniques to protect reference panel donors [26,39]. Specifically, SHIELD proceeds in two stages:
(i) Initial input perturbation to guarantee local differential privacy via randomized response.
(ii) Fitting a Hidden Markov Model (HMM) to each subsequent client query via the forward-backward algorithm [40- 44]. In an experiment that closely simulates a real-world use case for haplotype imputation; we show that SHIELD is able to obtain stateof-the-art imputation accuracy while providing mathematically formalized privacy guarantees. Such results suggest that perturbation via differential privacy holds significant promise for straightforward inclusion as an unobstructed component of standard genomic workflows in which algorithmic accuracy is nonetheless retained.
Materials and Methods
Overview
The setting for which SHIELD is intended consists of a client user uploading target genomes to a public imputation server [12]. In the standard imputation workflow, contributors to a bio bank upload their sequenced genomic data to a central, publicly available server, where the data are then collated to create a haplotype reference panel to pass as an argument to an imputation algorithm [1,3,4]. Subsequently, client researchers may then upload target genomes as part of a clinical study to the server, where the targets are imputed using the private haplotype reference panel and, most often, an algorithm based in HMMs and the forward-backward algorithm [23,28-31,43,44]. At no point in the workflow is the haplotype reference panel directly visible to client researchers submitting jobs to the server. However, while the privacy of the contributors to the reference panel may appear guaranteed, it has been demonstrated that adversarial attacks employing carefully coordinated queries to the server can divulge the sequences of reference haplotypes (Table 1) [12]. To this end, SHIELD modifies the imputation workflow by leveraging local [40], differential privacy [35-37,41,45]. Haplotype data can be represented as a bit string in which a 1 at the itch position in the sequence indicates that the haplotype possesses the minor allele at the site and a 0 the major allele [29]. Prior to submission to the central imputation server, pseudorandom noise is added to the two bitstrings denoting each individual’s pair of haplotypes randomized response, a technique from differential privacy that simply consists of flipping a random subset of the bits from 0 to 1 and vice versa [41,42]. The likelihood that a given bit in the haplotype bitstring is flipped varies as a function of a parameter ε called the privacy budget such that lower values of ε entail a higher probability that any bit is flipped and therefore a higher degree of privacy [38]. The trade-off, however, is that lower privacy budgets incur a greater expense to imputation accuracy, rendering it a hyper parameter that the database curator must carefully adjust to strike an acceptable balance between donor privacy and client utility. Once all perturbed haplotypes are collected at the central server, imputation is subsequently performed using the modified haplotypes as a reference panel.
| Notation | Significance |
|---|---|
| 0,1, and φ | Major allele, minor allele, and unobserved site |
| n and m | Number of reference samples and reference markers |
| [n] | Set of reference haplotypes |
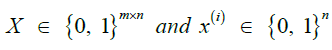 |
Reference panel in matrix form and the values at site i |
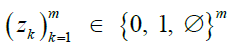 |
Reference panel in matrix form and the values at site i |
 |
Observed target haplotype sequence |
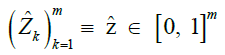 |
Sequence of imputed haplotype dosages |
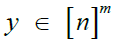 |
Site-wise identities of reference haplotypes from which 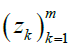 is descended is descended |
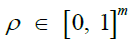 |
Recombination rates [26,39] |
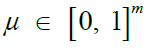 |
Mutation rates [26,39] |
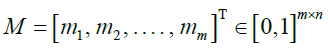 |
Emission probabilities |
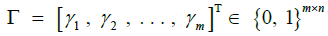 |
Posterior probabilities for haplotype identity |
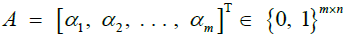 |
Forward probabilities [44], for haplotype identity |
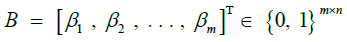 |
Backward probabilities [44], for haplotype identity |
Table 1: Notation employed in the development of Impute
Privacy is guaranteed by the fact that no contributor’s data will, on average, be unmodified when input to the imputation algorithm
invoked by client researchers. In this way, no adversary could be
certain that the results that they obtain from an attack accurately
reflect the true reference panel. These privacy guarantees are also
local; even if an adversary were to access the reference panel directly
rather than through coordinated queries, the data obtained would
again not perfectly reflect any individual’s true genome [45]. The
SHIELD algorithm consists of two subroutines, perturb and Impute
that are described below. The former is called once on a reference
panel X to produce a locally differentially private reference panel 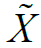 that is stored on the imputation server, whereas the latter is then called by the client for each subsequent query haplotype
that is stored on the imputation server, whereas the latter is then called by the client for each subsequent query haplotype 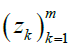
using 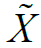 as the reference panel [35–38,40]. We outline the latter
first before proving the fact that SHIELD satisfies the stipulations
of differential privacy.
as the reference panel [35–38,40]. We outline the latter
first before proving the fact that SHIELD satisfies the stipulations
of differential privacy.
HMM-based genotype imputation
Like many imputation algorithms, SHIELD fits an HMM to haplotype queries. For a more detailed discussion on the Li- Stephens model of genetic recombination and imputation, see Li et al. 2003 [39], and Li et al. 2009, [26]; only a brief outline of the implementation in SHIELD is provided below. In sum, under the Li-Stephens model, target haplotypes are assumed to be mosaics of the multiple ancestral haplotypes from which they are descended. Two processes are assumed to be responsible for the creation of this mosaic, namely mutation and recombination described subsequently.
Given m sites (Table 1), we are given an observed target haplotype sequence 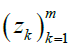 where the kth allele may be either major (0), minor (1), or missing
where the kth allele may be either major (0), minor (1), or missing 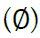 . We are given a reference panel X consisting of n reference haplotypes. Our goal is to compute the most likely true sequence
. We are given a reference panel X consisting of n reference haplotypes. Our goal is to compute the most likely true sequence 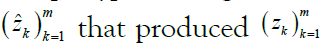 given our reference panel X; in other words, we compute the expected value
given our reference panel X; in other words, we compute the expected value
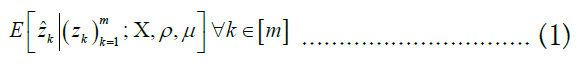
Where, ρ and μ are additional parameters described below.
The approach of HMM-based imputation is to perform ancestral haplotype inference, i.e., to assume that the genetic material at each site i descended from an ancestor in the reference panel X, denoting the ancestor of the target at the site yi. We therefore compute the posterior probability distribution of the random variable γk, effectively a vector of probabilities γk such that jth component of γk denotes the probability that the ancestor of the target at site i is the reference haplotype j:
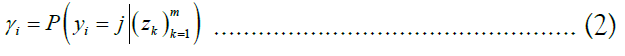
We stack these distributions for all sites into a matrix Γ. The utility of this approach lies in the fact that is equal to the sum product of the posterior probability distribution over the vector of all ancestors and each ancestor’s respective allele. Employing the law of the unconscious statistician, we may write this equality as an inner product:
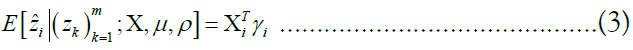
The relationship between consecutive vectors γi and γi+1 are described by a Markov random field. Under the Li-Stephens model, at each site i, a recombination event might occur, splitting the haplotype into fragments descended from two separate ancestors and resulting in the inequality yi+1 6= yi. Additionally, a mutation event may occur in which the allele possessed by the target may differ from the genetic material that it inherited from its respective ancestor at i, inverting the expected value. These two events are expressed by the probabilities
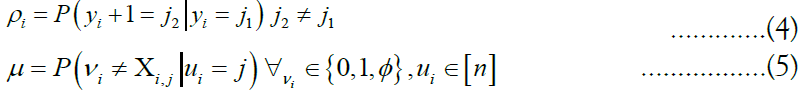
Which are concatenated to form the vectors ρ and μ, called the
recombination and mutation rates, respectively. Note that mutation
rates are defined for any possible target (vk) m k=1 with any possible ancestor ui. To compute the probability 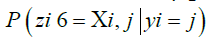 for a particular (zk) m k=1, we generate a matrix of emission probabilities M such that
for a particular (zk) m k=1, we generate a matrix of emission probabilities M such that
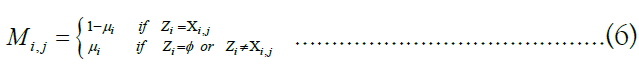
Reflecting the lack of information provided by a missing site valued 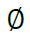 by defaulting to a uniform vector mi such that
by defaulting to a uniform vector mi such that 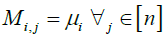 .
.
The posterior probabilities are computed by dividing them into
two separate probabilities, known as the forward and backward
messages and denoted, for the ith site, αi and βi, respectively. Loosely speaking, they reflect the information conveyed by the subsequences 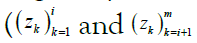 . The forward and backward messages are so-called because they are computed via dynamic programming] by iterating in opposite directions, that is, by stepping forward left-to-
right along the target and computing α1, α2, . . ., αm and by stepping backward right-to-left and computing βm, βm−1, . . ., β1 [46]. Respectively, the recurrence relations employed are
. The forward and backward messages are so-called because they are computed via dynamic programming] by iterating in opposite directions, that is, by stepping forward left-to-
right along the target and computing α1, α2, . . ., αm and by stepping backward right-to-left and computing βm, βm−1, . . ., β1 [46]. Respectively, the recurrence relations employed are
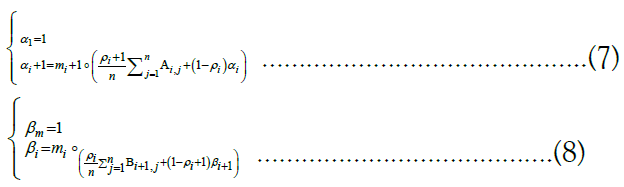
Finally, the forward and backward messages can be multiplied together component-wise and then normalized to derive the posterior probabilities:
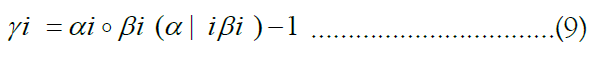
This gives rise to the final formulation of Impute below, which employs matrix-notation for brevity
Algorithm 1: Uses forward-algorithm to impute dosages according to Li-Stephens model.

else
Mi,j ← μi
end if
end for
end for
α1 ← 1
for i = 1, 2, . . . , m do
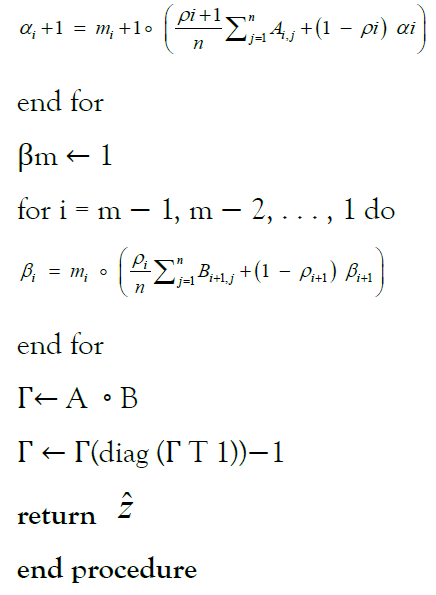
Differential privacy and randomized response
We derive the privacy guarantees of SHIELD from the notion of differential privacy [35–38]. Preliminarily, we develop the notion of neighboring datasets. Given a universe of datasets X, we say that two datasets x, y ∈ X are neighbours if and only if they differ by at most one individual sample. We will also call a randomized algorithm M: X → F, where F is an arbitrary probability space, a mechanism. We then say that a mechanism M: X →F satisfies (∈, δ)-differential privacy if and only if for all S ⊆ F and for all x, y ∈ X such that x are y are neighbouring, we have
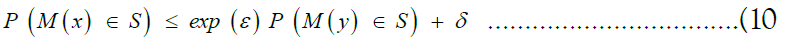
Among the most common techniques in differential privacy, randomized response satisfies ∈- differential privacy for binary attributes [41,42]. The randomized response scheme on a binary attribute X is a mechanism Mrr: {0, 1} → {0, 1} characterized by a 2 × 2 distortion matrix
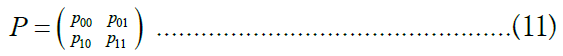
Where,
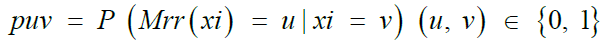 . It can be shown [41], that the highest-utility value for P is
. It can be shown [41], that the highest-utility value for P is
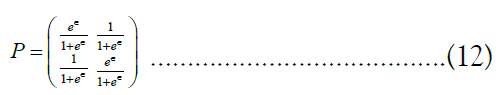
Fixing the number of samples in our reference panel n and the
number of sites m, we denote the universe of possible reference
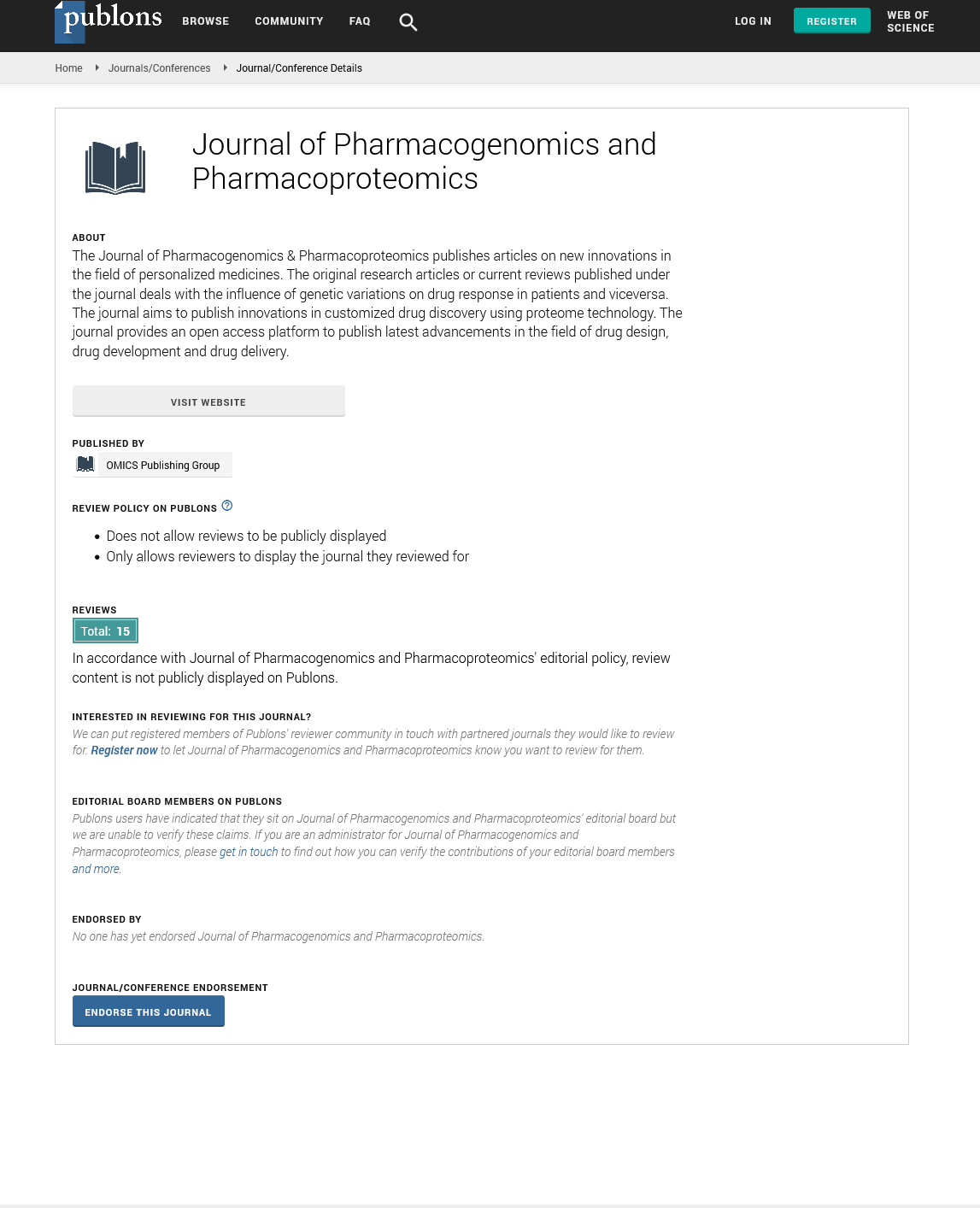
panels X={0, 1}m×n. Because haplotypes are vector-valued, applying
the notion of neighboring datasets is non-trivial. For our purposes,
we will say that two reference panels X, X’ ∈ X are neighbouring if
and only if their Hamming distance is less than or equal to 1. In
other words, we consider X and X’ neighbours if and only if Xi,j
≠X’I,j for a single marker i and a single individual j as opposed to
a whole-genome interpretation of neighboring datasets in which X and X’ may differ by an entire row. It then follows that by
applying the randomized response mechanism Mrr to each entry
in a reference panel matrix X, we may store a perturbed copy of
the original reference panel that satisfies entry-wise ε-differential
privacy. The perturbation step of SHIELD then consists of the procedure Perturb. We note that we use the symbol  to denote a pseudorandom sample and Bern (ϑ) to denote a Bernoulli distribution with parameter ϑ.
to denote a pseudorandom sample and Bern (ϑ) to denote a Bernoulli distribution with parameter ϑ.
Algorithm 2
Applies randomized response mechanism to reference panel.
Procedure PERTURB (X; ε)
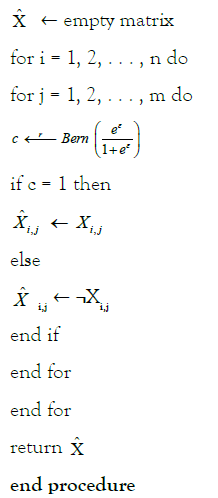
A convenient property of differential privacy is post-processing [35]. If M: X → F is an (ε, δ)- differentially private randomized algorithm and f: F → F’ is an arbitrary mapping, then f ◦ M: X → F’ is (ε, δ)-differentially private. This allows us to prove the following Theorem 1.
Theorem 1.
Given a reference panel X, pair of indices (i, j), Markov parameters ρ and μ, finite set of queries 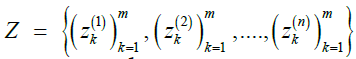 , and privacy budget ε>0, the mechanism given by
, and privacy budget ε>0, the mechanism given by

We then have M=f ◦ M’. Trivially, M’ satisfies ε-differentially private with respect to Xi,j. Because f is deterministic, we are able to apply post-processing, from which it follows that M is differentially private. Note that because each element of the set returned by f is conditioned only on the same output M’, the subroutine Perturb is called once, meaning that we do not consume an additional amount of ε (Figure 1).
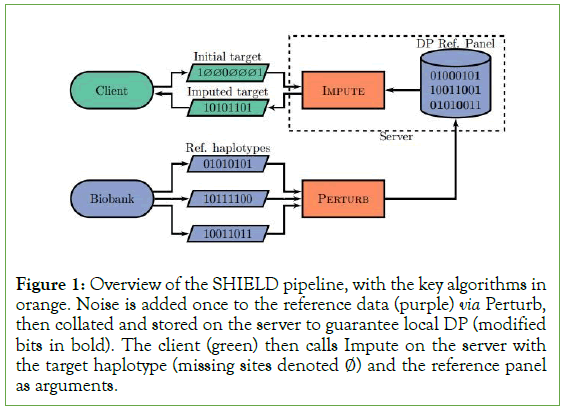
Figure 1: Overview of the SHIELD pipeline, with the key algorithms in orange. Noise is added once to the reference data (purple) via Perturb, then collated and stored on the server to guarantee local DP (modified bits in bold). The client (green) then calls Impute on the server with the target haplotype (missing sites denoted ∅) and the reference panel as arguments.
Case study: 1,000 genomes reference panel
To evaluate SHIELD’s performance on a realistic simulation of an imputation query, we performed an ablation study on the 1KG Phase 3 dataset [4]. We withheld 100 genomes (equivalent to 200 haplotypes) from the reference panel to impute via the remaining 2,404 samples. The first 10,000 single-nucleotide polymorphisms (SNPs) were extracted from 1KG; the remaining were discarded to render run times more tractable. To simulate an array-based assay of the 200 target haplotypes, we ablated all sites except those included in the Illumina Human1M-Duo v3.0 DNA Analysis Bead Chip manifest, the intersection of which with the first 10,000 sites in the 1KG data consisted of a total of 253 sites for an a priori coverage of 2.53%. To quantify accuracy, we summed the imputed dosages for each pair of haplotypes to compute a final genotype dosage for each sample, then computed the coefficient of determination (R2) between the genotype dosages and the ground-truth exome data. Because sites vary massively by minor allele frequency (MAF), the loci were divided into three bins corresponding to MAFs of (0%, 0.5%), (0.5%, 5%), and (5%, 50%). Respectively, these bins contained 5,943, 2,157, and 1,900 variants in the reference set. Accuracy was assessed, by bin, both to compare the performance of SHIELD to that of Minimac 3 and to characterize the effect of the privacy budget on our method’s accuracy [29].
Results
Modern imputation accuracy
Our analyses show nearly identical performance between SHIELD and Minimac 3 when no input perturbation is applied, with the former obtaining scores of 0.571, 0.784, and 0.902, respectively, on the three bins enumerated above and the latter scores of 0.584, 0.787, and 0.901 (Figure 2). SHIELD’s accuracy was reevaluated at various values of our privacy budget along the interval (0.01, 10), reflecting the typical range of values that ε is assigned in many differentially private algorithms [35]. Expectedly, accuracy exhibits a negative association with ε. At an upper bound of ε=10, SHIELD performs nearly identically to Minimac3 (0.564, 0.784, 0.901), while performance degrades significantly at ε = 0.01 (0.014, 0.038, 0.218) (Figure 3A).
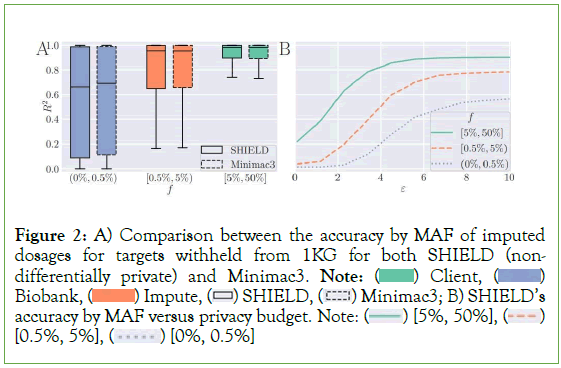
Figure 2: A) Comparison between the accuracy by MAF of imputed
dosages for targets withheld from 1KG for both SHIELD (nondifferentially
private) and Minimac3. Note:  Biobank,
Biobank,  Minimac3; B) SHIELD’s accuracy by MAF versus privacy budget. Note:
Minimac3; B) SHIELD’s accuracy by MAF versus privacy budget. Note:  [0.5%, 5%],
[0.5%, 5%],  [0%, 0.5%]
[0%, 0.5%]
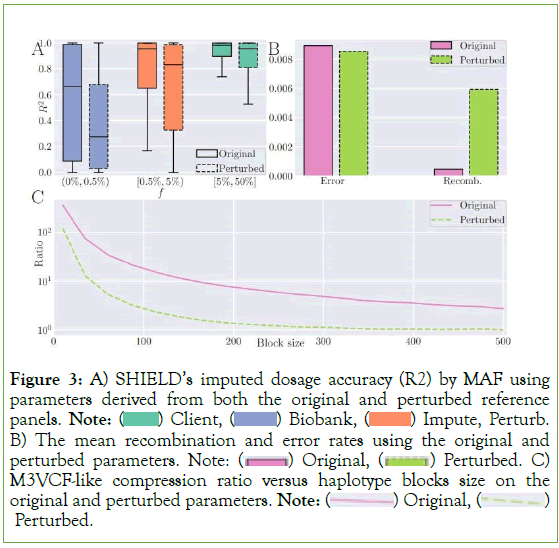
Figure 3: A) SHIELD’s imputed dosage accuracy (R2) by MAF using parameters derived from both the original and perturbed reference panels. Note:  Impute, Perturb. B) The mean recombination and error rates using the original and perturbed parameters. Note:
Impute, Perturb. B) The mean recombination and error rates using the original and perturbed parameters. Note:  Perturbed. C) M3VCF-like compression ratio versus haplotype blocks size on the original and perturbed parameters. Note:
Perturbed. C) M3VCF-like compression ratio versus haplotype blocks size on the original and perturbed parameters. Note: 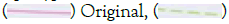 Perturbed.
Perturbed.
Impact on Markov parameters
As noted above, the parameters for the Markov random field modelling genomic recombination, namely the mutation and recombination rates, were computed on the unperturbed data by Minimac3 [29,39,43].
Noise added to the reference panel appeared to mimic the behavior of extremely rapid genomic recombination, causing Minimac3’s expectation-maximization procedure to dramatically overestimate the recombination rates (5.93 × 10-3 vs. 4.84 × 10-4) and, conversely, to underestimate the mutation rates (Figure 3B). These atypical rates exerted a decidedly negative impact on imputation accuracy, with performance decreasing by 35.5%, 16.1%, and 5.46% for each of the three bins, respectively, when the rates were computed on the reference panel perturbed at ε=5.0. In sum, it is clearly superior to estimate population parameters a priori, although, notably, doing so on the reference panel itself is not differentially private and may leak information.
Impact on compression rates
An additional feature of haplotype imputation introduced by Minimac3 was the M3VCF format for genomic data, which both substantially decreases total file size over the traditional VCF format and enables the state-space reduction technique that further improves imputation runtime [29]. The key insight enabling the format is the observation that, due to identity-by-descent, most haplotypes share identical k-mers of genomic material at intervals of contiguous loci despite being unique overall [26]. In other words, given an arbitrary interval along the genome, the number of unique k-mers collectively exhibited by the reference panel is almost always smaller than the total number of reference haplotypes per se. Therefore, it is possible to implement a compression scheme in which the genome is partitioned into intervals and only the unique k-mer strings are retained, substantially compressing the original reference panel [29]. An unfortunate consequence of local differential privacy via randomized response is that, on average, random noise will destroy the exact equality between haplotypes substrings. From the perspective of a compression algorithm attempting to identify the set of unique k-mers along a given interval, an apparently larger number of unique fragments will exist, rendering M3VCF-style compression will less efficient. As an illustration, we partitioned the genomic data into mutually exclusive, exhaustive blocks of uniform size ranging from 2 to 500. We then computed the data compression ratio when M3VCF-style state-space reduction was applied at each block size by dividing the total 5.008 × 108 bits in the uncompressed panel by the number of bits following compression and plotted the ratio against block size (Figure 3C). Input perturbation resulted in compression rates up to an order of magnitude smaller.
Discussion
Though the noise added by some differentially private mechanisms may destroy utility entirely, we observe that SHIELD is conveniently able to return highly accurate results in spite of its strong privacy guarantees [37]. This is likely in part due to the fact that randomized response tends to outperform other basic mechanisms like Laplace in standard applications; hence, it is not only the simplest approach to differentially private algorithms, but often the most effective as suggested by the results presented in this work [41]. Another cause for SHIELD’s high performance is likely that inherent to the Li-Stephens algorithm itself, which is intended to in part to account for a nontrivial level of noise in genomic datasets. As an inherently noisy problem with robust solutions, imputation is thus well-suited for the perturbation introduced by pseudorandom mechanisms. Still, however, the fact that SHIELD is able to achieve its performance on a relatively small reference panel of less than 2,500 individuals is quite remarkable given the comparatively large number of SNPs involved in the study and the rarity of some of the variants involved. With some biobanks now containing hundreds of thousands of samples, it is reasonable to presume that performance in many contexts may be even higher still [1]. We note that the strong performance of SHIELD parallels the effectiveness of RAPPOR, a differentially private algorithm for mining strings in commercial contexts that is also based on randomized response [47]. Unlike SHIELD, however, RAPPOR is not intended for data that is inherently binary; rather, arbitrary alphanumeric strings are hashed onto Bloom filters [48], that are subsequently perturbed. The fact that haplotype data intrinsically consist of bitstrings makes randomized response particularly convenient in a genomic context. But despite the strong performance exhibited in the experiments above, we note three significant limitations to our algorithm. First, it should be acknowledged that the privacy guarantees made by our program are limited to individual variants. In other words, for a given privacy budget ε [35-37], SHIELD can provably ensure protection for each sample’s genotype at any one site, but not across the entire genome per se. Certain adversarial attacks are therefore still feasible with SHIELD even though accurate reconstruction of reference haplotypes is not [13-15,17,18]. Whole-genome privacy would instead require the division ε across each site (see for a discussion on composition in differential privacy), which is prohibitively difficult for datasets containing tens of thousands of variants [36]. On the other hand, such divisions may be possible if a fairly limited segment of the genome is to be imputed. Future research into genomic privacy may investigate these scenarios or alternative differentially private mechanisms. Further, our program is dependent on accurate a priori estimates of population parameters which are non-trivial to compute while still enforcing local differential privacy [42]. Subsequent work may inquire into the feasibility of computing population parameters a posteriori by performing some manner of statistical correction [26,29,39]. Finally, SHIELD does not natively implement state-space reduction techniques featured in programs like Minimac3 to significantly reduce compute times [12-15,17,33-37]. Furthermore, it is unclear how effective such subroutines would be if included in SHIELD given the substantial impact that randomized responses exerts on reference panel compression rates. In other words, additive noise mechanisms may simply render such forms of lossless clustering impractical altogether [19-26,49,50].
Conclusion
In this work, we develop Secure Haplotype Imputation Employing Local Differential privacy (SHIELD), a program for performing genomic imputation with strong privacy guarantees for reference haplotypes via the randomized response mechanism [42]. Analysis shows that SHIELD is able to obtain modern accuracy in realistic experimental settings at typical privacy budgets, demonstrating that differential privacy may be readily incorporated into genomic workflows with minimal impact on the utility of downstream results. Although the risk of highly accurate breaches of human subject privacy in spite of existing confidentiality protocols is growing in genomic research, differential privacy offers a mathematically cogent and robust solution [12-15,17,33-37]. The capacity for differentially private imputation to straightforwardly return accurate queries as demonstrated above is highly promising for the prospect of privacy in practical genomic medicine. Given that imputation is only one of many stages in a typical biostatistics pipeline, however, subsequent work may expand on SHIELD by applying differential privacy to other forms of genomic analysis, including GWAS, haplotype phasing, and genome annotation [19-26,49,50]. The development of a complete suite of algorithms enabling end-to-end private clinical studies would constitute a major step towards addressing the urgent challenge that is securing sensitive genomic data from de-anonymization and other adversarial attacks.
Acknowledgement
We thank Hoon Cho at the Broad Institute of MIT and Harvard for insightful discussion.
References
- Sudlow C, Gallacher J, Allen N, Beral V, Burton P, Danesh J. UK biobank: An open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med. 2015;12(3):e1001779.
[Crossref] [Google Scholar] [Pubmed]
- Philippakis A, Smoller JW , Jenkins G , Dishman E. All of us research program investigators. The “All of Us” research program. N Engl J Med. 2019;381(7):668-676.
[Crossref] [Google Scholar] [Pubmed]
- McCarthy S, Das S, Kretzschmar W, Delaneau O, Wood AR, Teumer A “A reference panel of 64,976 haplotypes for genotype imputation. Nat Genet. 2016;48(10):1279-1283.
[Crossref] [Google Scholar] [Pubmed]
- Siva N. 1000 Genomes project. Nat Biotechnol. 2008;26(3):256-257.
[Crossref] [Google Scholar] [Pubmed]
- Staying on track with Health TracksSM. 2023.
- Ancestry® helps you understand your genealogy. 2023.
- Where will your DNA take you?. 2023
- Broad Institute of MIT and Harvard. 2023
- Cloud Life Sciences API. 2023.
- Pathology genomics workspace. 2023.
- Act A. Health insurance portability and accountability act of 1996. US Statut Large. 1996;21:104-191.
- N. Dokmai, C. Kockan, K. Zhu, X. Wang, S. C. Sahinalp, H. Cho. Privacy-preserving genotype imputation in a trusted execution environment. Cell Syst. 2021;12(10), 983-993.
[Crossref] [Google Scholar] [PubMed]
- Bonomi L, Huang Y, Ohno-Machado L. Privacy challenges and research opportunities for genomic data sharing. Nat Genet. 2020;52(7):646-654.
[Crossref] [Google Scholar] [PubMed]
- S. Sankararaman, G. Obozinski, M. I. Jordan, E. Halperin. Genomic privacy and limits of individual detection in a pool. Nature genetics. 2009;41(9):965-967.
[Crossref] [Google Scholar] [PubMed]
- N. Homer, S. Szelinger, M. Redman, D. Duggan, W. Tembe, J. Muehling, et al. Resolving individuals contributing trace amounts of DNA to highly complex mixtures using high-density snp genotyping microarrays. PLoS Genet. 2008; 4(8):e1000167.
[Crossref] [Google Scholar] [PubMed]
- Dinur I, Nissim K. Revealing information while preserving privacy. In Proceedings of the twenty-second ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems. 2003:202-210.
- Y. Erlich, T. Shor, I. Pe’er, S. Carmi. Identity inference of genomic data using long-range familial searches. Science. 2018:362;690-694.
[Crossref] [Google Scholar] [PubMed]
- Gymrek M, McGuire AL, Golan D, Halperin E, Erlich Y. Identifying personal genomes by surname inference. Science. 2013;339(6117):321-324.
[Crossref] [Google Scholar] [PubMed]
- Visscher PM, Brown MA, McCarthy MI, Yang J. Five years of GWAS discovery. Am J Hum Genet. 2012 Jan 13;90(1):7-24.
[Crossref] [Google Scholar] [PubMed]
- Korte A, Farlow A. The advantages and limitations of trait analysis with GWAS: A review. Plant methods. 2013;9(1):1-9.
[Crossref] [Google Scholar] [PubMed]
- Visscher PM, Wray NR, Zhang Q, Sklar P, McCarthy MI, Brown MA, et al. 10 years of GWAS discovery: biology, function, and translation. Am J Hum Genet. 2017;101(1):5-22.
[Crossref] [Google Scholar] [PubMed]
- International HapMap Consortium. A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449(7164):851.
[Crossref] [Google Scholar] [PubMed]
- Marchini J, Howie B, Myers S, McVean G, Donnelly P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat Genet. 2007;39(7):906-913.
[Crossref] [Google Scholar] [PubMed]
- Servin B, Stephens M. Imputation-based analysis of association studies: Candidate regions and quantitative traits. PLoS Genet. 2007;3(7):e114.
[Crossref] [Google Scholar] [PubMed]
- Taliun D, Harris DN, Kessler MD, Carlson J, Szpiech ZA, Torres R, et al. Sequencing of 53,831 diverse genomes from the NHLBI TOPMed Program. Nature. 2021;590(7845):290-299.
[Crossref] [Google Scholar] [PubMed]
- Li Y, Willer C, Sanna S, Abecasis G. Genotype imputation. Annu Rev Genomics Hum Genet. 2009;10:387-406.
[Crossref] [Google Scholar] [PubMed]
- J. Marchini, B. Howie. Genotype imputation for genome-wide association studies. Nat Rev Genet. 2010;11(7 ):499-511.
[Crossref] [Google Scholar] [PubMed]
- Li Y, Willer CJ, Ding J, Scheet P, Abecasis GR. MaCH: Using sequence and genotype data to estimate haplotypes and unobserved genotypes. Genet Epidemiol. 2010;34(8):816-834.
[Crossref] [Google Scholar] [PubMed]
- Das S, Forer L, Schönherr S, Sidore C, Locke AE, Kwong A, et al. Next-generation genotype imputation service and methods. Nat Genet. 2016;48(10):1284-1287.
[Crossref] [Google Scholar] [PubMed]
- Ayres DL, Darling A, Zwickl DJ, Beerli P, Holder MT, Lewis PO, et al. BEAGLE: An application programming interface and high-performance computing library for statistical phylogenetics. Syst Biol. 2012;61(1):170-173.
[Crossref] [Google Scholar] [PubMed]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, et al. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81(3):559-575.
[Crossref] [Google Scholar] [PubMed]
- Scheet P, Stephens M. A fast and flexible statistical model for large-scale population genotype data: applications to inferring missing genotypes and haplotypic phase. Am J Hum Genet. 2006;78(4):629-644.
[Crossref] [Google Scholar] [PubMed]
- H. Cho, D. J. Wu, B. Berger. Secure genome-wide association analysis using multiparty computation. Nature biotechnology. 2018;36:547-551.
- Naveed M, Ayday E, Clayton EW, Fellay J, Gunter CA, Hubaux JP, et al. Privacy in the genomic era. ACM Comput Surv. 2015;48(1):1-44.
[Crossref] [Google Scholar] [PubMed]
- Dwork C. Differential privacy. In International colloquium on automata, languages, and programming 2006;1-12.
- Dwork C. Differential privacy: A survey of results. In International conference on theory and applications of models of computation. 2008;1-19.
- Dankar FK, El Emam K. Practicing differential privacy in health care: A review. Trans. Data Priv. 2013;6(1):35-67.
- Dwork C, Roth A. The algorithmic foundations of differential privacy. Foundations and Trends® in Theoretical Computer Science. 2014;9(4):211-407.
- Li N, Stephens M. Modelling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics. 2003;165(4):2213-2233.
[Crossref] [Google Scholar] [PubMed]
- Yang M, Lyu L, Zhao J, Zhu T, Lam KY. Local differential privacy and its applications: A comprehensive survey. arXiv preprint arXiv. 2020.
- Wang Y, Wu X, Hu D. Using randomized response for differential privacy preserving data collection. InEDBT/ICDT Workshops. 2016;1558:0090-6778.
- S. L. Warner. Randomized response: A survey technique for eliminating evasive answer bias. J Am Stat Assoc. 1965; 60(309):63-69.
[Crossref] [Google Scholar] [PubMed]
- Rabiner L, Juang B. An introduction to hidden Markov models. Ieee Assp Magazine. 1986;3(1):4-16.
- Baum LE. An inequality and associated maximization technique in statistical estimation for probabilistic functions of Markov processes. Inequalities. 1972;3(1):1-8.
- Cormode G, Jha S, Kulkarni T, Li N, Srivastava D, Wang T. Privacy at scale: Local differential privacy in practice. In Proceedings of the 2018 International Conference on Management of Data. 2018;1655-1658.
- Bellman R. Dynamic programming. Science. 1966;153(3731):34-37.
[Crossref] [Google Scholar] [PubMed]
- Erlingsson Ú, Pihur V, Korolova A. Rappor: Randomized aggregatable privacy-preserving ordinal response. In Proceedings of the 2014 ACM SIGSAC conference on computer and communications security. 2014;1054-1067.
- Bloom BH. Space/time trade-offs in hash coding with allowable errors. Communications of the ACM. 1970;13(7):422-426.
- Browning SR, Browning BL. Haplotype phasing: Existing methods and new developments. Nat Rev Genet. 2011;12(10):703-714.
[Crossref] [Google Scholar] [PubMed]
- L. Stein. Genome annotation: From sequence to biology. Nat Rev Genet. 2001;2(7): 493-503.
[Crossref] [Google Scholar] [PubMed]
Citation: Harary M (2023) Secure Haplotype Imputation Employing Local Differential Privacy. J Pharmacogenom Pharmacoproteomics. 14:076.
Copyright: © 2023 Harary M. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.