Indexed In
- RefSeek
- Directory of Research Journal Indexing (DRJI)
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Scholarsteer
- Publons
- Euro Pub
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Research Article - (2023) Volume 9, Issue 1
Numerical Investigation on Diffusion Length, Suspending Time, and Forces Acting on COVID-19 Virus Particles in an Indoor Environment
Mahdi Bagherian Dehaghi* and Mehrzad ShamsReceived: 03-Nov-2022, Manuscript No. CMBO-22-18615; Editor assigned: 07-Nov-2022, Pre QC No. CMBO-22-18615 (PQ); Reviewed: 21-Nov-2022, QC No. CMBO-22-18615; Revised: 10-Feb-2023, Manuscript No. CMBO-22-18615 (R); Published: 17-Feb-2023, DOI: 10.35841/2471-2663.23.9.150
Abstract
The purpose of this study is to study two-dimensional CFD simulations of the COVID-19 virus two phase flows in steady air with the Euler-Lagrange method. This was accomplished by developing CFD programs in MATLAB and simulations in COMSOL software. Brownian, drag, saffman, and weight forces are considered for studying the dynamics of virus flow. In order to study the motion of viruses, brownian, drag forces, and the weight of viruses play an important role. In this study, three different diameters of virus particles were considered, with three different initial conditions and three different initial velocities. The diffusion length and suspending time of viruses in the air have been computed in each of the nine states.
Keywords
CFD; Two phase flow; COVID-19 virus; Euler-lagrange method; Diffusion length; Suspending time
Introduction
The transmission of infectious respiratory diseases has always been a topic of interest in recent decades and has attracted much attention from various disciplines [1,2]. Viruses are transmitted primarily through the air [3]. As viruses travel through the air, they are spread by infected individuals exhaling, and then transmitted to healthy individuals by inhaling the air [4]. During exhalation activities, such as talking, coughing, and sneezing, many drops of saliva and secretions are released into the air through the respiratory system (mouth and nose). It has been demonstrated that talking and coughing plays an important role in producing respiratory droplets. These droplets and their residues after evaporation can transmit respiratory infectious diseases [5]. Coughing is one of the symptoms of infectious respiratory diseases such as influenza and SARS [6]. Viruses adhere to saliva droplets and respiratory tract secretions. Due to this reason, salivary droplets and the secretions of the respiratory system play a significant role in the spread of respiratory diseases. Since many people spend most of their time indoors, if there are pathogenic viruses in the indoor environment, they are more likely to suffer from viral (respiratory) diseases such as influenza, SARS-CoV-2, and colds.
Materials and Methods
The particle size plays a significant role in determining how particles move and how long they remain suspended in the air. During coughing and sneezing, droplets with diameters of up to 200 microns are emitted. In the air, large droplets settle very quickly. Thus, these droplets contribute to the spread of disease to those close to the patient. The smaller droplets remain suspended in the air for longer and are more effective at transmitting diseases over long distances [7]. In addition to the fact that during coughing or sneezing, the diameter of the initial droplets emitted is different, the modeling of the emitted droplets has indicated that up to 50% of the initial volume of the droplet evaporates, and if the diameter of the droplets is less than 20 microns, this phenomenon occurs instantly [8]. Since the droplets with a diameter of 30 microns or less are very small, the effect of gravity or inertia on them can be ignored, and their displacement is primarily influenced by the airflow field. A droplet with a diameter of 50 microns to 200 microns, which is highly affected by gravity, falls when the airflow in the ambient environment weakens. Droplets with a diameter of 300 microns or more are more affected by inertia and gravity. Droplets with a diameter of 500 microns mostly move in a straight path.
The velocity of saliva droplets and respiratory tract secretions is another factor that influences their movement. People cough and sneeze at a velocity ranging from 1.5 m/s to 28.8 m/s, with an average velocity of 10.2 m/s [9]. PIV (particle image velocimetry) was used in 2006 to measure the coughing velocity of people, and the initial cough velocity was reported to be between 6 m/s and 22 m/s, with an average velocity of 11.2 m/s. Chao and colleagues reported in 2009 that the average cough velocity was 11.7 m/s using the PIV method. The maximum velocity caused by sneezing in men is 100 m/s, while coughing ranges from 16 m/s to 48 m/s [10]. In addition, the average air velocity during conversation is 3.9 m/s [11].
In most cases, the transmission of airborne viruses is predicted using CFD (computational fluid dynamics) simulations. CFD simulations are not expensive, and accurate determination of boundary conditions is essential. Zhu, et al. performed CFD simulation, which assumed steady state flows in a room with static air and modeled the spread of saliva droplets due to coughing using Lagrangian equations. This research showed that saliva droplets with a total mass of 6.7 milligrams are released at a maximum velocity of 22 m/s. These particles travel in static air at least 2 meters.
The concentration of virus particles in the air is one of the factors that increase the risk of infectious respiratory diseases. The mouth produces between 112 drops and 6720 drops during speaking, approximately 947 drops to 2085 drops per cough. It is estimated that droplet concentrations range from 2.4 cm3 to 5.2 cm3 per coughing and from 0.004 cm3 to 0.223 cm3 per talking as a result of coughing and talking, respectively [12].
As the size and velocity of particles released from the respiratory system during exhalation activities vary widely, in this study, COVID-19 particles of 60 nm and 5 microns were considered. In addition, initial velocities of 5.20 m/s and 45 m/s were considered for each of the diameters mentioned. CFD solution and Lagrangian approach for particles have been implemented to simulate the forces applied to the virus particles, the time the COVID-19 suspension time in the air, and the length of their diffusion. It should be noted that the virus particles were considered aerosol particles with the mentioned diameters.
The purpose of this study is to simulate the movement of COVID-19 virus particles. Since the concentration of virus particles is diluted, the Euler-Lagrange method has been applied. As a result of the high computational cost of this method, a twodimensional space has been used to simulate an indoor environment in which the person is located in this space. This two-dimensional geometry has dimensions of 2 meters by 12 meters, and an individual of 1.8 meters in height is located at the end of the geometry. Additionally, the 5 cm cross-sectional room at the height of 1.7 meters to 1.75 meters from the ground level is used to model the mouth as the entry point for fluid and COVID-19 particles.
According to the introduction, we used the following assumptions:
• The room does not have a temperature gradient.
• The virus particles are spherical.
• Droplets emitted from the respiratory system are assumed to have a diameter of 60 nm or 5 microns, corresponding to the size of virus particles. Additionally, these droplets are considered to be water, with water density and viscosity.
• Assuming no air conditioning system is installed in the room, fluid flow in the room is considered to be static.
• The particle's velocity when leaving the respiratory system is the same as the airflow leaving the respiratory system. This study investigated velocities of 5 m/s, 20 m/s, and 45 m/s.
• According to previous research, which was also mentioned in the introduction, the number of COVID-19 virus particles released from the respiratory system is assumed to be 6000.
• An explicit numerical solution is applied.
• The discretization of the velocity derivative term is secondorder Euler.
• Due to the dilution of virus particles, the Euler-Lagrange approach has implemented one-way couplings between the air and virus particles.
Governing equations
In fluid dynamics, the Reynolds number is one of the most important dimensionless numbers. It can be calculated using the following equation:

This research examines the effects of weight, drag force, brownian force, and saffman lift force, which contribute significantly to COVID-19 transmission.
Drag force: Stokes drag force with Cunningham correction factor is as follows.

Cc is Cunningham's correction factor. That can be calculated as follow.

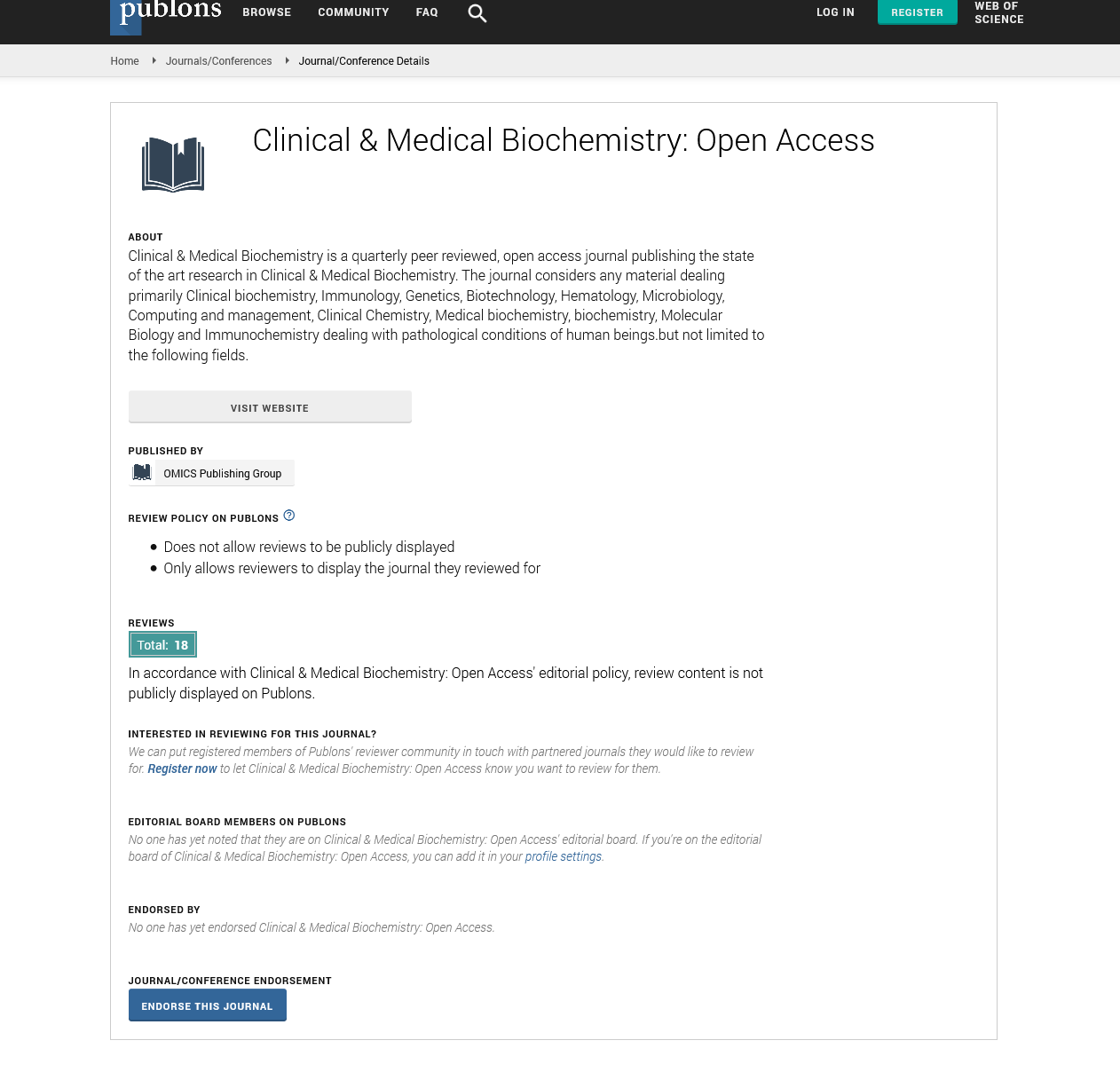
Saffman lift force: Particles are subjected to a force called the saffman force when there is a high velocity gradient. A force almost occurs near the walls, causing particles to move away from them. According to saffman's force relationship:
Brownian force: For small particles, inertia and weight forces are negligible, but there is another force, the Brownian force, which is a stochastic force in different magnitudes and directions. The following equations show the calculation of this force.



Generating Gaussian random numbers using random numbers between 0 and 1 (U1, U2):

The magnitude of brownian force and weight are as follows, respectively.


Force balance for COVID-19 virus particles:


Discretization and numerical solution:
The velocity derivative is discretized as follows


This problem is solved by discretizing the aforementioned relations and considering the time step (τ) as 0.1.
Equations (19) and (20) are numerical relations used in MATLAB programming. Also, to compute the velocity, the discretized form of momentum is used as follows.
with the following time step: Δt=0.1 τ
Results and Discussion
As a result of executing the numerical computational code for multiple time steps to solve the problem for both 5 microns and 60 microns diameter, and comparing the results of these runs, we conclude that the results of the problem are highly dependent on the time step. The appropriate time step based on several repetitions is 0.1 and 0.01 for virus particles with diameters of 60 nm and 5 microns, respectively.
From the MATLAB code, different results are obtained, including the average and variance of saffman lift forces, Brownian forces, drag forces, and weight forces acting on 6000 virus particles in two directions with respect to time, x, and y. Additionally, the average and variance location of 6000 virus particles with respect to time, x, and y.
Figure 1 shows the drag force in the y direction on the virus particle with a diameter of 60 nm in terms of time for 1176 seconds of program execution; the virus leaves the mouth at a velocity of 45 m/s. The maximum diffusion length and suspending time for COVID-19 particles obtained from the Euler-Lagrange method with MATLAB programming for particles with a diameter of 5 microns and 60 nm are given in Tables 3 and 4, respectively (Tables 1and 2).
| Initial velocity | Maximum diffusion length for COVID-19 particles |
Maximum suspending time for COVID-19 particles |
|---|---|---|
| 5 m/s | 0.56 m | 146 s |
| 20 m/s | 2.47 m | 146 s |
| 45 m/s | 5.97 m | 146 s |
Table 1: Maximum suspending time and diffusion length of the COVID-19 virus in the air (diameter 5 μm at an angle of 0℃, taking into account the brownian force and for 6000 particles of the coronavirus with MATLAB).
| Initial velocity | Maximum diffusion length for | Maximum suspending time for COVID-19 particles |
|---|---|---|
| 5 m/s | 1.02 m | 1175 s |
| 20 m/s | 4.32 m | 1175 s |
| 45 m/s | 8.73 m | 1175 s |
Table 2: Maximum suspending time and diffusion length of the COVID-19 virus in the air (diameter 60 nm at an angle of 0℃, taking into account the Brownian force and for 6000 particles of the coronavirus with MATLAB).
Figure 1: The drag force in the y direction on the virus particle with a diameter of 60 nm in terms of time for 1176 seconds of program execution, the virus leaves the mouth at a velocity of 45 m/s.
In Tables 3 and 4, due to the consideration of Fick's law, the diffusion length is slightly greater than the specific results of the MATLAB program
| Initial velocity | Maximum diffusion length for COVID-19 particles | Maximum suspending time for COVID-19 particles | Diffusion length of first settled COVID-19 droplets | Suspending time of first settled COVID- 19 droplets |
|---|---|---|---|---|
| 5 m/s | 1.15 m | 1171.7 s | 4.5 cm | 247.37 s |
| 20 m/s | 4.61 m | 1176.6 s | 5.1 cm | 265.6 s |
| 45 m/s | 10.14 m | 1179.7 s | 5.9 cm | 272.4 s |
Table 3: Maximum suspending time and diffusion length of COVID-19 virus in the air, suspending time and diffusionlength of first settled COVID-19 droplets (diameter 60 nm at an angle of 0℃, taking into account the Brownian force and for 6000 particles of the coronavirus with COMSOL multi-physics).
| Initial velocity | Maximum diffusion length for COVID-19 particles | Maximum suspending time for COVID-19 particles | Diffusion length of first settled COVID-19 droplets | suspending time of first settled COVID- 19 droplets |
|---|---|---|---|---|
| 5 m/s | 0.7 m | 140.54 s | 1.5 cm | 50.3 s |
| 20 m/s | 2.81 m | 145.56 s | 3.4 cm | 59.37 s |
| 45 m/s | 6.32 m | 170.6 s | 4.1 cm | 64.37 s |
Table 4: Maximum suspending time and diffusion length of COVID-19 virus in the air, suspending time and diffusion length of first settled COVID-19 droplets (diameter 5 μm at anangle of 0℃, taking into account the Brownian force and for 6000 particles of the coronavirus with COMSOL multi-physics).
The results of each table for particles with the same diameter show that the suspending time of virus particles does not depend on the initial velocity of the particles, so the suspending time at different velocities is almost equal, which is valid for both MATLAB and COMSOL results. The results of each table for particles with the same diameter show that the diffusion length increases with the increase of the initial velocity of the virus particles.
Conclusions
In this research, the dynamic of COVID-19 viruses in an indoor environment is simulated by the Euler-Lagrange method with CFD programming in MATLAB software and modeling in COMSOL Multi physics commercial finite element software. The following is determined based on programming results in MATLAB software and CFD simulation in COMSOL software.
In static air, the maximum suspending time and diffusion length of the COVID-19 virus are determined for viruses with a diameter of 60 nm at 45 m/s initial velocities, about 10.14 meters, and approximately 20 minutes.
• As the initial velocity of virus particles increases, the diffusion length of virus particles with the same diameter increases.
• There is no relationship between the suspension time and the initial velocity of virus particles of the same diameter, so the suspension time at different velocities is nearly the same.
• Particles are under the influence of inertia at the initial distance of their movement. During the second phase of their movement, the brownian force and oscillations of the particles increase dramatically due to the weakening of the exhaled air flow and the reduction of inertia in the x direction.
• The Brownian force is independent of time and y in the x and y directions.
• Due to the decrease in the relative velocity difference between the particles and the fluid, the drag force in the x direction decreases linearly.
• A reduction in inertia in the x direction at the end of the initial diffusion phase leads to an increase in the brownian force in the x direction. As a result of this increase, particle fluctuations in the x-axis increase. As a result of these fluctuations, the relative velocity of the particles increases, causing the drag force to fluctuate in the y direction.
Reference
- Holmes NS, Morawska L. A review of dispersion modelling and its application to the dispersion of particles: an overview of different dispersion models available. Atmos Environ. 2006;40(30):5902-5928. [Crossref] [Google Scholar]
- Gupta JK, Lin CH, Chen Q. Flow dynamics and characterization of a cough. Indoor Air. 2009;19(6):517-525. [Crossref] [Google Scholar] [PubMed]
- Morawska L. Droplet fate in indoor environments, or can we prevent the spread of infection? Indoor Air 2005: Proceedings of the 10th International Conference on Indoor Air Quality and Climate. Tsinghua University Press. 2005;9-23. [Crossref] [Google Scholar] [PubMed]
- Cole EC, Cook CE. Characterization of infectious aerosols in health care facilities: an aid to effective engineering controls and preventive strategies. Am J Infect Control. 1998;26(4):453-464. [Crossref] [Google Scholar]
- Garner JS. Guideline for isolation precautions in hospitals. The Hospital Infection Control Practices Advisory Committee. Infect Control Hosp Epidemiol. 1996;17(1):53-80. [Crossref] [Google Scholar] [PubMed]
- Zhu S, Kato S, Yang JH. Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment. Build Environ. 2006;41(12):1691-1702. [Crossref] [Google Scholar]
- Xie X, Li Y, Sun H, Liu L. Exhaled droplets due to talking and coughing. J R Soc Interface. 2009;6(suppl_6):S703-714. [Crossref][Googlescholar][PubMed]
- VanSciver M, Miller S, Hertzberg J. Particle image velocimetry of human cough. Aerosol Sci Technol. 2011;45(3):415-422. [Crossref] [Google Scholar]
- Wells W F. Airborne Contagion and Air Hygiene: An Ecological Study of Droplet Infection. Harvard University Press for the Commonwealth Fund, Cambridge, England. 2–3. [Google Scholar]
- Chao CY, Wan MP, Morawska L, Johnson GR, Ristovski ZD, Hargreaves M, et al. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. J Aerosol Science. 2009;40(2):122-133. [Crossref] [Google Scholar] [PubMed]
- Badeau A, Afshari A, Goldsmith T, Frazer D. Preliminary prediction of flow and particulate concentration produced from normal human cough dispersion. In Proceedings of the Second Joint 24th Annual Conference and the Annual Fall Meeting of the Biomedical Engineering Society, Engineering in Medicine and Biology. 2002;246-247. [Crossref] [Google Scholar]
- Bourouiba L. Turbulent gas clouds and respiratory pathogen emissions: Potential implications for reducing transmission of COVID-19. JAMA. 2020;323(18):1837-1838. [Crossref] [Google Scholar] [PubMed]
Citation: Dehagh MB, Shams M (2023) Numerical Investigation on Diffusion Length, Suspending Time, and Forces Acting on COVID-19 Virus Particles in an Indoor Environment. Clin Med Bio Chem. 9:150.
Copyright: © 2023 Dehagh MB, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.