International Journal of Swarm Intelligence and Evolutionary Computation

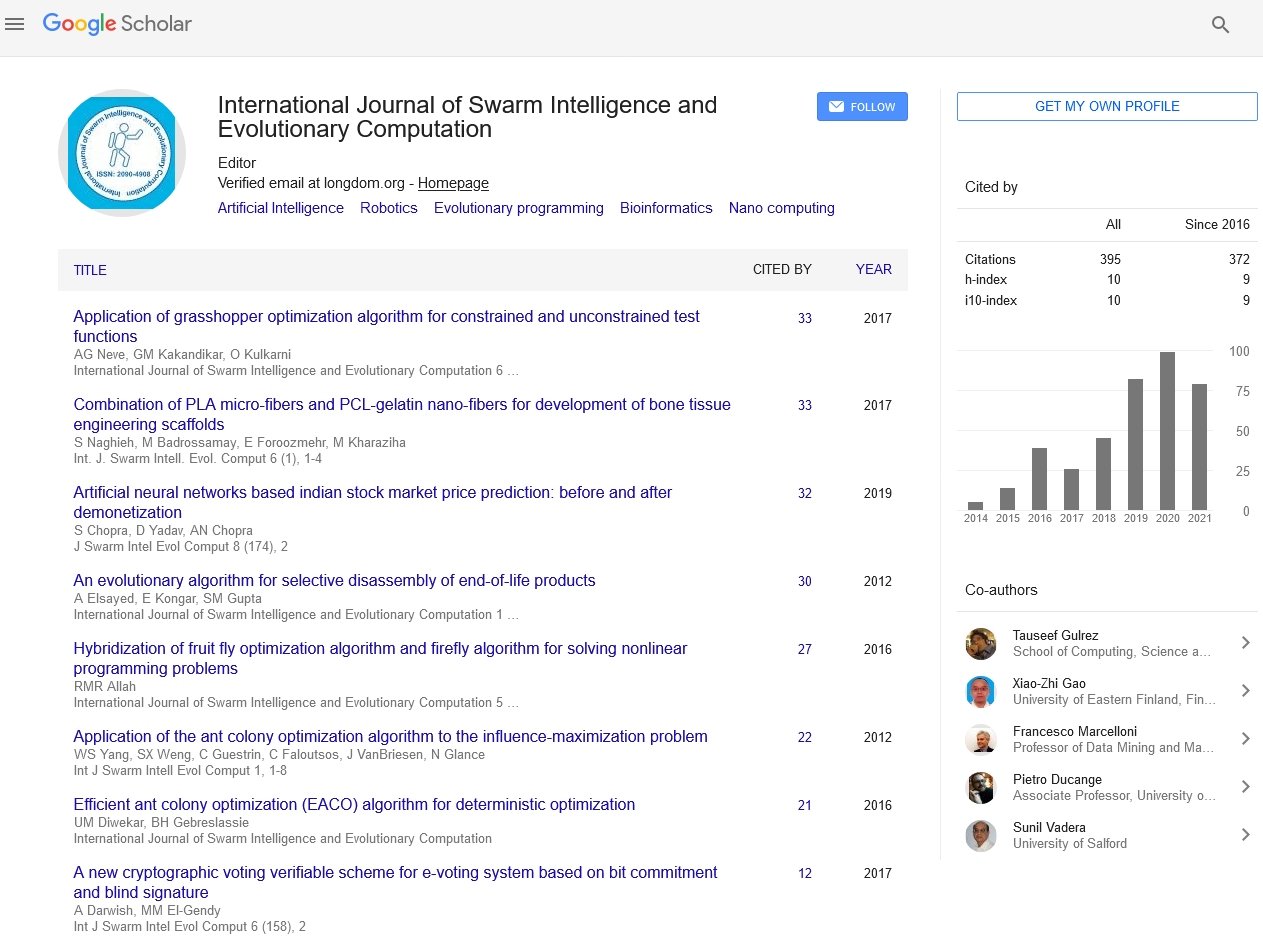
Multi-Objective Programming and Balancing Multiple Objectives for Optimal Decision Making

Nehant Mishra^* Department of Bioinformatics, University of Pondicherry, Puducherry, India
^*Correspondence: Nehant Mishra, Department of Bioinformatics, University of Pondicherry, Puducherry, India, Email:

Received: 02-Jan-2023, Manuscript No. SIEC-23-20392; Editor assigned: 04-Jan-2023, Pre QC No. SIEC-23-20392 (PQ); Reviewed: 18-Jan-2023, QC No. SIEC-23-20392; Revised: 26-Jan-2023, Manuscript No. SIEC-23-20392 (R); Published: 03-Feb-2023, DOI: 10.35248/2090-4908.23.12.299

Description

Multi-objective programming is a powerful technique for solving complex decision-making problems where multiple objectives need to be balanced. It involves finding the optimal solution that satisfies multiple conflicting objectives. In many real-world decision-making problems, there are multiple objectives that need to be balanced. For example, in production planning, the objective may be to minimize the production cost while maximizing the production rate. In such cases, a single objective optimization technique may not be sufficient, and need to consider multiple objectives simultaneously. Multi-objective programming is a powerful technique that helps us address such complex decision-making problems. Multi-objective programming is a technique for solving optimization problems with multiple objectives. It involves finding the optimal solution that satisfies multiple conflicting objectives. In multi-objective programming, seek to find the set of solutions that represents the best trade-off between the various objectives.

The solutions obtained in multi-objective programming are known as Pareto optimal solutions. These solutions represent the best trade-off between the objectives, and no other solution can improve one objective without worsening another. The set of Pareto optimal solutions is known as the Pareto front.

Applications of multi-objective programming

Multi-objective programming has applications in various fields, including engineering, finance, and environmental management. In engineering, multi-objective programming is used to optimize the design of complex systems with multiple objectives, such as cost, performance, and reliability.

In finance, multi-objective programming is used to optimize investment portfolios with multiple objectives, such as risk and return. In environmental management, multi-objective programming is used to optimize resource allocation with multiple objectives, such as environmental impact and economic cost.

Techniques for multi objective programming

There are several techniques for solving multi-objective programming problems. The most popular techniques are:

Weighted sum method: In this method, assign weights to each objective, and the problem is transformed into a single-objective optimization problem.

Goal programming: In this method, set goals or constraints for each objective, and the problem is transformed into a constrained optimization problem.

Evolutionary algorithms: In this method, use evolutionary algorithms, such as genetic algorithms and particle swarm optimization, to search for the Pareto optimal solutions.

Challenges in multi-objective programming

Multi-objective programming has several challenges, including:

Complexity: Multi-objective problems are often complex and involve a large number of variables and constraints.

Trade-offs: There are often trade-offs between the objectives, and finding the optimal trade-off can be challenging.

Visualization: Visualizing the Pareto front can be difficult when there are more than three objectives.

Future directions in multi-objective programming

There are several future directions of research in multi-objective programming, including:

Hybrid methods: Combining multiple techniques to solve multi-objective problems more efficiently.

Interactive methods: Developing interactive methods that involve the decision-maker in the optimization process.

Big data: Developing techniques for handling multi-objective problems with large data sets.

Conclusion

Multi-objective programming is a powerful technique for solving complex decision-making problems where multiple objectives need to be balanced. It involves finding the optimal solution that satisfies multiple conflicting objectives. Multi-objective programming has applications in various fields, including engineering, finance, and environmental management. There are several techniques for solving multi-objective programming problems, including the weighted sum method, goal programming, and evolutionary algorithms. Multi-objective programming has several challenges, including complexity, tradeoffs, and visualization. The future directions of research in multi-objective programming include hybrid methods, interactive methods, and big data.