Indexed In
- Open J Gate
- JournalTOCs
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Scholarsteer
- Publons
- Geneva Foundation for Medical Education and Research
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
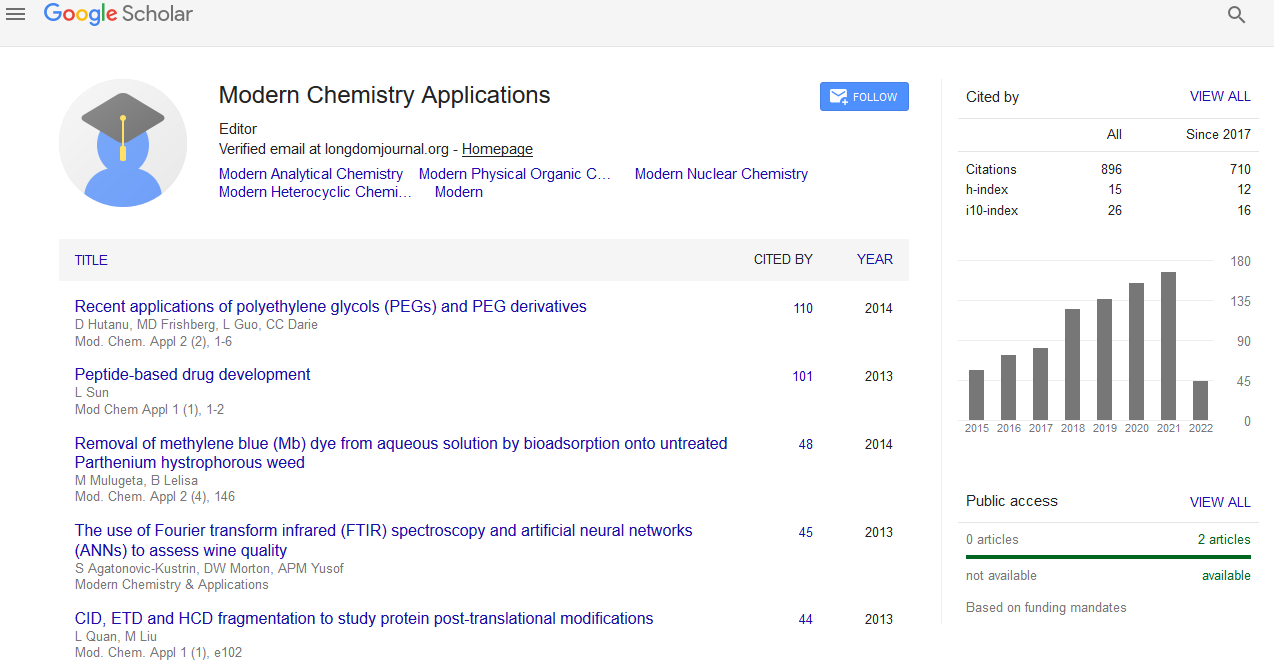
Research - (2022) Volume 10, Issue 11
Modeling of Tartrazine Dye Adsorption onto Treated and Untreated Cocoa Shell by Non-Linear Regression Methods
Michele Nana Nemgne1, Alain Paul Nanssou Kouteu2,3, Donald Raoul Tchuifon Tchuifon2*, Christian Sadeu Ngakou1, Ndifor-Angwafor George Nche1 and Anagho Solomon Gabche12Department of Process Engineering, Laboratory of Energy, Materials, Modeling and Method, National Higher Polytechnic School of Douala, University of Douala, Douala, Cameroon
3Process Engineering Laboratory, Ucac-Icam Institute, Douala, Cameroon
Received: 15-Nov-2022, Manuscript No. MCA-22-18791; Editor assigned: 18-Nov-2022, Pre QC No. MCA-22-18791 (PQ); Reviewed: 02-Dec-2022, QC No. MCA-22-18791; Revised: 09-Dec-2022, Manuscript No. MCA-22-18791 (R); Published: 16-Dec-2022, DOI: 10.35248/2329-6798.22.10.383
Abstract
Tartrazine is a toxic industrial dye, and it is reported to affect water quality and is harmful to human health. The objective of this study is to contribute to elaborate less expensive adsorbents from cocoa shell for the elimination of tartrazine from aqueous solution. The effects of initial pH (2-8), contact time (0-90 min), mass of adsorbent (10-70 mg) and the nature of treatment were evaluated on the adsorption of tartrazine. The optimal conditions for the adsorption of tartrazine on all the substrates are pH=2, contact time=60 min, amount of adsorbent=40 mg. Nonlinear regression analysis showed the best fit for pseudo second order kinetics regardless of material with Chi-square (χ2) test values of 0.1672, 0.0811 and 0.0366 respectively for CC-H2O, CC-HNO3 and CC-H3PO4. Equilibrium data were fitted to two-parameter mono-solute models and mono-solute three-parameter models. Adsorption isotherm data were best described by Jovanovic model for water washed substrate, Langmuir model for phosphoric acid treated substrate and Dubinin-Radushkevich model for treated substrate to nitric acid for the 2-parameter isotherms. As for the three-parameter isotherms, it is the Khan model that better describes the data for the substrate washed with water and the substrate treated with phosphoric acid, whereas the Redlich-Peterson model was found for the substrate treated with nitric acid.
Keywords
Adsorbents; Tartrazine yellow dye; Isotherm model; Kinetics; Non-linear regression
INTRODUCTION
Dyes are widely used in industries such as textiles, rubber, paper, plastics, cosmetics, etc., to color their products. The dyes are invariably left as the major waste in these industries. Due to their chemical structures, dyes are resistant to fading on exposure to light, water and many chemicals and, therefore, are difficult to be decolorized once released into the aquatic environment [1,2]. Many of the organic dyes are hazardous and may affect aquatic life and even the food chain. One of them is tartrazine (C.I. Acid Yellow 23, AY23) which is an anionic azo dye whose presence in thousands of foods and drugs has been reported as a possible cause of asthma, urticaria, and angioedema [3,4]. It also has phototoxic potential [3]. The removal of dyes from industrial waste before they are discharged into the water bodies is therefore very important from health and hygiene point of view and for environmental protection. Various techniques have been employed for the removal of dyes from wastewaters such as, ion exchange, electrolysis, membrane processes, flocculation, Advanced Oxidation Processes (AOP), coagulation, photocatalytic processes, biological treatments and adsorption [5,6]. Conventional physical and chemical methods are either costly, or produce concentrated sludge, or may not be capable of treating large volumes of effluent without the risk of clogging. Natural materials that are available in abundance, or certain waste products from industrial or agricultural operations, may have great potential as an inexpensive sorbent [7,8]. The linear regression method has long been used to determine the best-fitting models and the least squares method has been used to find the parameters of the models [9-12]. After plotting a linear regression, the parameters are calculated from the slope and the intersection of the line. The adsorption kinetics and isotherm model with the best fit for the adsorption data is selected based on the correlation coefficient (R2) [13]. The most significant disadvantage of linear regression is the non-fixed error distribution [14,15]. Also, in case of kinetics and isotherms with more than two parameters, we cannot calculate the value of unknown parameters using linear regression and graphical method [14].
More recently, the non-linear regression method in conjunction with error analysis as an alternative to linear regression has been used to create a model in adsorption studies [16]. Several error analysis methods such as residual Root Mean Square Error (RMSE), nonlinear chi-square test error function (χ2), coefficient of determination (R2) were introduced for nonlinear analysis [17,18].
Due to their low cost, after these materials have been expended, they can be disposed of without expensive regeneration. In this study, cocoa shell untreated and treated with nitric acid and phosphoric acid were used for the biosorption of tartrazine from water. The optimization of sorption parameters, sorption isotherms and kinetics were investigated in batch mode.
Methodology
Collection and preparation of adsorbent and adsorbate
Cocoa shell was collected from Kekem, in the Haut-Nkam division, West region of Cameroon. It was washed with tap water, grinded in a mill and sieved (100 μm). The treatment was made with concentrates phosphoric acid and nitric acid (5.10-3 M). In a flask, 10 g of cocoa shell and 100 ml of each acid were put together. After 2 hours of agitation (200 trs/min), the mixture was filtered, and the adsorbent was washed several times with distilled water. It was then dried in an oven at about 80°C to remove moisture and grinded before it was used as adsorbent of tartrazine dye.
Characterization of adsorbents
The three absorbents were characterized by determining the following parameters: Functional groups, moisture content, loss of mass on ignition, pH and bulk density, the zero-point charge using standard procedures.
Fourier transform infrared: Adsorbents were characterized by Infrared Fourier Transform Spectroscopy to identify the functional groups and chemical bonds of the adsorbents and their participation in tartrazine dye adsorption. The FT-IR was recorded in the wave number range 4000-400 cm-1 using a Bruker, Alpha-P Spectrometer in Attenuated Total Reflectance mode.
Moisture contents: It was done by weighing 10 g of each adsorbent into a crucible. This was placed in the oven at constant temperature of 105°C until obtained a constant mass. The sample was then removed and put rapidly into a desiccator to prevent more moisture uptake from atmosphere. The sample was re-weighed. The ratio of the mass lost by the powder to its original mass gave the moisture content of the sample [19].

Where W1 is the weight of crucible, W2 is the initial weight of crucible with sample, and W3 is the final weight of crucible with sample.
Bulk density (g/cm3): The bulk density of each of the samples was determined using Archimedes’ principle, by weighing a measuring cylinder before and after filling with the samples. The measuring cylinder was then dried, and the sample was packed inside the measuring cylinder, leveled, and weighed. The weight of the sample packed in the measuring cylinder was determined from the difference in weight of the filled and empty measuring cylinder. The volume of water in the container was determined by taking the difference in weight of the empty and water filled measuring cylinder. The bulk density was determined using the equation below [20].

Where W1 is the weight of empty measuring cylinder, W2 is the weight of cylinder filled with sample, and V is the volume of cylinder.
pH and zero point charge (pHzpc): pH of zero charge, pHzpc, corresponds to the pH at which the surface charge is null. pHzpc of the cocoa shell was estimated according to standard procedure. 15 ml of a decimolar solution of NaCl was introduced each into a reactor each containing 50 mg of cocoa shell to be analyzed. The pH of each solution was adjusted by addition of decimolar solutions of NaOH or HCl (by varying values of pH between 2 and 12). pHzpc was determined by the intersection point of the representative curves pH (final)=f[pH (initial)] and the first bisector curve. Stirring was maintained at 27°C for 48 hours with the aid of a multi-agitator system. The contents of the reactors were then filtered with Whatman N°4 filter paper after which the pH of the final solutions was measured [21].
Sorption experiment
The dye tartrazine was used without further purification. A stock solution of 500 mg/lit of tartrazine was made by dissolving the required amount of the dye in distilled water. Several standard solutions were made from the stock solution in concentration range 10 to 50 mg/lit and a calibration curve was drawn by measuring the absorbance at λmax=428 nm using a JENWAY visible spectrophotometer. The experiments were done adjusting the pH of the solutions with decimolar nitric acid and sodium hydroxide. The batch adsorption was carried in 100 ml conical flasks by mixing a pre-weighed amount of the cocoa shell with 15 ml of aqueous dye solution of a particular concentration. The conical flasks were kept on a shaker and were agitated for a pre-determined time interval at a constant speed 150 trs/min. The system parameters such as pH, agitation time, adsorbent amount, and concentration were controlled during the experiments. After adsorption was over, the mixture was filtered and the residual concentration of the filtrate was analyzed using a spectrophotometer (JENWAY, model 6715). The amount of adsorbed (mg/g) was calculated using the formulae below:

Where Qe is the amount of solute adsorbed from the solution, V is the volume of the adsorbate, Ci is the initial concentration of tartrazine, Cf is the concentration after adsorption, and m is the weight in gram of the adsorbent.
The removal efficiency was determined by computing the percentage sorption using the formulae in the Equation (4) below

Effect of initial pH: To determine the effect of the initial pH, 40 mg of the adsorbent was agitated in a 15 ml aqueous solution of 40 mg/lit of tartrazine, in the pH range of 2.0-8.0 pH adjustment was done by adding either HCl or NaOH. After 1 hour, the solution was rapidly filtered, and the residual concentration determined by spectrophotometer. The amount (Qe) of tartrazine adsorbed was calculated by using equation (3).
Effect of contact time: The effect of agitation time on the adsorption process was determined by agitating 40 mg of ground adsorbent in a 15 ml solution of tartrazine of initial concentration 40 mg/lit for different time intervals. At each time, the solution was rapidly filtered, and the residual concentration determined by spectrophotometer. The percentage removal (%) of tartrazine was calculated by using Equation (4).
Effect of amount of adsorbent: In this set of experiments, different masses of the adsorbents ranging between 10 to 70 mg were agitated with 15 ml solution of tartrazine of initial concentration 40 mg/lit during the equilibrium time.
Effect of biosorbent treatment: To investigate the effect of biosorbent treatment, adsorption of tartrazine on biosorbent was carried out using 40 mg of biosorbent, 15 ml of solution of concentration 40 mg/lit at initial pH=2, agitation speed 150 rpm at 60 min (equilibrium time).
Batch equilibrium experiments: Isotherm experiments were carried out by agitating 15 ml of tartrazine dye of concentration ranging from 10 to 50 mg/lit with 40 mg of each biosorbent in a 100 ml flask at room temperature at optimum pH of 2 and a constant agitation speed of 150 rpm for 60 minutes. The data collected were fitted to the pseudo-first order kinetic model, pseudo-second order kinetic model, and intraparticle diffusion kinetic models. To determine the best adsorption model, initial concentration and their adsorption capacities were fitted to two kinds of models: Two parameter monosolute model (Langmiur model, Freundlich model, Temkin model, Dubinin-Radushkevish model and Redlish- Peterson model) and Momo-solute three-parameter models (Redlish-Peterson model, Sips model, Toth model, Hill’s model and Kahn’s model).
The comparison of literature models for adsorption isotherms and reaction kinetics was based on a statistical calculation of several error function among the most used in the literature: Residual moot Mean Square Error (RMSE), nonlinear chi-square test error function (χ2), Coefficient of determination (R2), Hybrid fractional error function (HYBRID).
Adsorption kinetics
Several kinetics models were tested to determine the best kinetics model of the adsorption of tartrazine on the biosorbents.
Pseudo-first-order model: The pseudo-first order equation is generally expressed in [22].

With K1: Adsorption rate constant (g/mg.min); Qe: quantity adsorbed at equilibrium (mg/g) and Qt: quantity adsorbed at time t (mg/g).
The pseudo-second-order model: The pseudo-second order chemisorption kinetic equation [23].

With K2: Pseudo-second order adsorption rate constant (g/ mg.min); Qe: quantity adsorbed at equilibrium (mg/g) and Qt: quantity adsorbed at time t (mg/g).
Elovich’s model: The Elovich equation is generally expressed [24].

To simplify the Elovich equation, Chien and Clayton in 1980 assumed that αβt >>>>1 and applying the initial conditions qt=0 to t=0 the equation (7) becomes

With α: The initial adsorption rate (g/mg.min); β: desorption rate constant (g/mg.min) and Qt: Amount adsorbed at time t (mg/g).
Intraparticular diffusion: The intraparticular diffusion model is expressed as equation (9) [24].

With Kid: Weber intraparticle diffusion rate constant in (mg/g min1/2); Qt: Amount adsorbed at time t (mg/g); C: value of the thickness of the boundary layer.
Adson isotherm
To determine the best adsorption model, initial concentration and their adsorption capacities were fitted to two kinds of models: Two parameter monosolute model and Momo-solute three-parameter models.
Two-parameter mono-solute models
Langmuir model: The Langmuir adsorption isotherm is often used for adsorption of a solute from a liquid solution.

With Qe: Amount adsorbed at equilibrium (mg/g); Qm: Maximum amount adsorbed at equilibrium (mg/g); Ce: Equilibrium concentration of the adsorbate in solution (mg/lit) and KL: Langmuir’s constant relates to the adsorption energy (Lit/mg).
Freundlich model: Freundlich equation is an equation based on the adsorption onto a heterogeneous surface

With Qe: Amount adsorbed at equilibrium (mg/g), Ce: Concentration of adsorbent at equilibrium (mg/L); KF and n are empirical constants.
Temkin model: Temkin isotherm model takes into account the effects of indirect adsorbate/adsorbate interactions on the adsorption process.

With A: Constant of the Temkin isotherm (Lit/mg); b: Variation in the heat of adsorption (kJ/mol); R: Perfect gas constant (8.314 J/mol.K); Ce: Concentration of the adsorbent at equilibrium (mg/ lit); Qe: quantity adsorbed at equilibrium (mg/g) and T: absolute temperature (K). The adsorption obeys the Temkin model if the determined coefficients are low.
Dubinin-radushkevich model: The model of D-R was developed for the adsorption of substances in trace amounts in aqueous phase onto porous solids.

With Qe: Amount adsorbed at equilibrium (mg/g); Qm: Maximum amount adsorbed at equilibrium (mg/g); Ce: Equilibrium concentration of the adsorbate in solution (mg/lit); K’: Constant linked to the adsorption energy (mol2K/J2) and ε: Polanyi potential (kJ/mol) its expression is given by equation (14)

With R: Ideal gas constant (R=8.314 kJ/mol.K) and T: The absolute temperature.
The adsorption energy can be obtained from the value of K’ using the following equation [25].

Jovanovic model: The Jovanovic model is predicated on the assumptions contained in the Langmuir model, but in addition the possibility of some mechanical contacts between the adsorbate and adsorbent [26].

With Qe: Amount adsorbed at equilibrium (mg/g); Qm: maximum amount adsorbed at equilibrium (mg/g); Ce: The adsorbent concentration at equilibrium (mg/lit) and KJ is the Jovanovic constant (Lit/mg).
2-mono-solute three-parameter models
Most of these models are derived from simple Langmuir and Freundlich models. Three parameter models were developed to improve the simulation of adsorption isotherms compared to two- parameter models.
Model of redlich-peterson: It is the most quoted and most used three-parameter model in the literature because it is applicable over a wide concentration range. It is an empirical equation developed by Redlich-Peterson to improve adaptation by the Langmuir and Freundlich equation. It approaches the Freundlich model for high concentrations and the Langmuir equation for low concentrations. It can be applied to both homogeneous and heterogeneous systems [27,28].
The Redlich and Peterson model is given by the following equation:

With Ce: equilibrium concentration (mg/L); Qe: quantity adsorbed at equilibrium (mg/g), A and B are the constants of the Redlich- Peterson model (Lit/mg); β: parameters of the Redlich and Peterson equation with β heterogeneity parameters, between 0 and 1. When the recovery rate is high, the equation can be reduced to the Freundlich equation in the following form [29]:

Hence A/B and (1-β) represents respectively the parameters KF and 1/n of the Freundlich equation.
Model of sips: Identifying the problem of continuously increasing adsorbed amount with increasing concentration in the Freundlich equation, Sips proposed an equation combining Freundlich and Langmuir isotherms. This produces an expression that has a finite limit at a high enough concentration. This model is valid for predicting heterogeneous adsorption and localized adsorption systems without adsorbate-adsorbate interactions. The Sips model for low concentrations is reduced to the Freundlich model. At high concentrations, the Sips model predicts the monolayer adsorption capacity, which is specific to the Langmuir isotherm. Also, for β=1, the Sips equation is reduced to the Langmuir model. The Sips model is expressed by the following equation [30].

βs: parameter of the Sips equation; as: adsorption equilibrium constant (Lit/g) and Ks: constant of the Sips model (L/g); Qe: amount adsorbed at equilibrium (mg/g) and Ce the adsorbent concentration at equilibrium (mg/lit).
Model of toth: The Toth model was established for adsorption in the gas phase, from the Langmuir isotherm, but considering that the surface of the adsorbent is not energetically homogeneous. In the liquid phase, it is generally used as an adaptation of the Langmuir model, close to the empirical Redlich-Peterson model. The model proposed by Toth is an empirical equation that describes many adsorption systems multilayer and heterogeneous systems. It is valid for low and high concentrations [31].
Toth’s equation is given by the following expression:

With KT and n the Toth isotherm constants (L/g); Qe: Amount adsorbed at equilibrium (mg/g); Qm: Maximum amount adsorbed at equilibrium (mg/g) and Ce: the adsorbent concentration at equilibrium (mg/lit)
If n=1, Toth’s equation is reduced to Langmuir’s equation. If it deviates from unity, the system is said to be heterogeneous [28].
Hill’s model: Hill in 1910 proposed an isothermal model from the non-ideal competitive adsorption model to define different adsorbent bonds on a homogeneous adsorbent surface. This isothermal model assumes that adsorption is basically a cooperative manifestation, including the ability to bind the ligand to one site on the macromolecule, influencing various binding sites on the same macromolecule [32,33].
The Hill isotherm can be represented as follows:

With nH and KD the Hill isotherm constants; QSH: Maximum adsorption capacity of the Hill isotherm (mg/g); Qe: Amount adsorbed at equilibrium (mg/g) and Ce: equilibrium concentration of the adsorbate in solution (mg/lit).
Kahn’s model: Kahn’s adsorption isotherm model is a general model for the adsorption of dilute pure solutions [34].
Kahn’s model is expressed by the following equation:

With ak and bk are constants of the Kahn isotherm model, Qmax is the maximum adsorption capacity of the Khan isotherm (mg/g); Qe: Amount adsorbed at equilibrium (mg/g) and Ce: Equilibrium concentration of the adsorbate in solution (mg/lit).
If equals ak=1, the above equation approximates the Langmuir isotherm and at higher concentration values this model reduces to the Freundlich isotherm.
Error functions
In this study, non-linear regression was applied using Microsoft Excel Solver function from Excel Microsoft 2013 for fitting the curve. The best fit for experimental data was determined from the coefficient of determination (R2), Residual root Mean Square Error (RMSE) and Chi-square test (χ2). The expressions of the error functions are given as follows [35-37].


Where Qe exp and Qe,cal (mg/g) are the equilibrium capacity of adsorption obtained from the experiment and by calculating from the model, respectively and N is the number of data points.
Results and Discussion
Characterization of adsorbents
IR spectra: The Fourier Transform InfraRed (FT-IR) spectroscopy method is used to investigate the presence of certain functional groups in a molecule. The spectra of cocoa shell washed with water and treated with phosphoric acid or nitric acid obtained are shown in Figure 1. Between 3650-3200 cm-1 is the -OH group vibration in the main constituents of lignocellulosic materials: Elongation vibration of the C-H aliphatic bonding in cellulose, hemicellulose, and lignin. Between 3000-2840 cm-1, with a high intensity at 2919 cm-1 meanwhile the adsorption band at 1603 cm-1 is attributed to a carboxylic function (C=O). 1500-1200 cm-1: O-H or -C-O deformation vibration of alcohols and -NO2 of aromatic nitro compounds; 1200-1000 cm-1: -C-O elongation vibration in carboxylic acids, lactones, esters, or aliphatic amines. Figure 1 shows that, all the spectra have the same peaks. This proves that both biosorbents have identical functional groups on their surfaces.

Figure 1: IR Spectra of cocoa shell washed with water (CC-H2O),
treated with phosphoric acid (CC-H3PO4) and treated with nitric acid
(CC-HNO3). Note:  CC-HNO3
CC-HNO3
Physicochemical parameters of the adsorbents: The water content of the substrates obtained from the acid treatment (nitric acid and phosphoric acid) varies from 4.48 to 4.55, values higher than that of the substrate washed with water which is 3.88. The bulk densities are not very different with values ranging from 0.35 to 0.37. The pH of the substrates all have acid pHs whatever the treatment used, but the acid treatments lead to the lowest values, 6.31 for the phosphoric acid treatment and 6.25 for the acid treatment nitrate against 6.51 for washing with water. On the other hand, for the pHzc which is an important characteristic illustrating the electrostatic interactions at the level of the surface of the adsorbents as a function of the pH of the medium, a notable difference is observed between that of the substrates treated with acids (6.74) and that washed with water (5.92). These results show that for pH values below 6.74, the surface of acid-treated substrates tends to be positively charged and if the pH is above 6.74, the surface tends to be negatively charged. For the substrate washed with water, the surface tends to be positively charged if the pH is lower than 5.92 and negatively if it is higher than 5.92. The values reported are in the range with those reported in the literature (Table 1) [38].
| Properties | CC-H2O | CC-H3PO4 | CC-HNO3 |
|---|---|---|---|
| % Moisture content | 3.88 | 4.48 | 4.55 |
| Bulk density (g/cm3) | 0.37 | 0.35 | 0.36 |
| pH | 6.51 | 6.31 | 6.25 |
| pHZPC | 5.92 | 6.74 | 6.74 |
Table 1: Some physicochemical parameters of the cocoa shell washed with water (CC-H2O), treated with phosphoric acid (CC-H3PO4) and treated with nitric acid (CC-HNO3).
Biosorption
Effect of initial pH: The adsorption characteristics of Tartrazine by cocoa shell were studied at varying pH range from 2 to 8. The profile concerning pH shows that in the observed pH range the adsorption capacity was much pronounced at lower pH 2, while as the pH increases adsorption decreases. This is attributed to the protonation of the fibers of the adsorbents at low values of pH in which H+ ions provide a significantly strong electrostatic attraction between the fibers surface and the dye molecules leading to maximum adsorption. The decrease in the adsorption capacity for the dye was attributed to two mechanisms: firstly, an electrostatic attraction between the protonated amino groups of absorbents and dyes; and secondly, the chemical interaction between tartrazine and adsorbents [14]. As such all subsequent studies were performed at pH 2, which is the optimum value for adsorption (Figure 2) [39].

Figure 2: Effect of initial pH on adsorption capacity of tartrazine on
cocoa shell washed with water (CC-H2O), treated with phosphoric acid
(CC-H3PO4) and treated with nitric acid (CC-HNO3) in the pH range
of 2.0-8.0. Conditions: C0=40mg/lit; m=40mg; t=60min; V=15ml; Speed=150rpm. Note:  CC-H3PO4.
CC-H3PO4.
Effect of contact time: The contact time between the adsorbate and adsorbent is an important parameter for designed adsorption process. The results show that the adsorption process took place in two phases. The first phase occurred very fast and takes place during the first 10 minutes of adsorption for CC-H3PO4 and CC- HNO3, and 20 minutes for CC-H2O. This is explained by the great availability of all the adsorption sites of the biosorbent. The second phase that occurred was less fast and takes place within 10-50 minutes for CC-H2O and 30 min pour CC-HNO3 and 60 min for CC-H3PO4 where the adsorption capacity at the equilibrium point. In this study, the equilibrium time necessary for adsorption was found approximately 60 min for all adsorbents (Figure 3).

Figure 3: Effect of contact time on adsorption capacity of tartrazine
by cocoa shell washed with water (CC-H2O), treated with phosphoric
acid (CC-H3PO4) and treated with nitric acid (CC-HNO3). Conditions:
C0=40mg/lit; pH=2; m=40mg; t=60min; V=15ml; Speed=150rpm. Note:  CC-H3PO4.
CC-H3PO4.
Effect of amount of adsorbent: Figure 4 shows the effect of adsorbent dose on the adsorption capacity of tartrazine dye by cocoa shell washed by water and treated by phosphoric acid or nitric acid. It is observed that removal efficiency increases with increase in the biosorbent. This can be mostly attributed to an increase in the adsorptive surface area and the availability of more active adsorption sites. Furthermore, at higher biosorbent dosage, there is a very fast adsorption onto the biosorbent surface. However, with increase in the biosorbent the quantity of dye adsorbed per unit weight of macrophyte gets reduced. A decrease in qe value with increasing biomass loading may be due to complex interactions of several factors such as availability of solute, interference between binding sites and electrostatic interactions [40].

Figure 4: Effect of adsorbent dose on the adsorption capacity of
tartrazine by cocoa shell washed with water (CC-H2O), treated with
phosphoric acid (CC-H3PO4) and treated with nitric acid (CC-HNO3).
Conditions: C0=40mg/lit; pH=2; t=60min; V=15ml; Speed=150rpm. Note:  CC-H3PO4.
CC-H3PO4.
Effect of biosorbent treatment: The treatment of the biosorbent can be an influence of the behavior of the biosorbent during the adsorption process. Figure 5 shows that the percentage of the dye removed by cocoa shell washed with water (CC-H2O) is greater than that of the treated materials (CC-H3PO4) and (CC-HNO3). This result can be explained by the fact that during the treatment, some components of the lingo cellulosic materials present before the treatment having great affinity towards amaranth red, has been solubilized or destroyed. However, it was observed that (CC- H3PO4) has a higher percentage adsorption than (CC-HNO3), which explains the fact that (CC-H3PO4) has more extractibles than (CC-HNO3). Moreover (CC-HNO3) has a better specific surface than (CC-H3PO4). This results clearly show that the adsorption of the dye doesn’t depend on the surface area but depends on the functional group on the biosorbent [16].

Figure 5: Effect of the treatment of coca shell on the adsorption
capacity of tartrazine. Cocoa shell washed with water (CC-H2O),
treated with phosphoric acid (CC-H3PO4) and treated with nitric acid
(CC-HNO3). Conditions: C0=40mg/lit; pH=2; m=40mg; t=60min; V=15ml; Speed=150rpm. Note:  CC-H3PO4.
CC-H3PO4.
Modeling of kinetic studies
Adsorption kinetics for the removal of tartrazine dye in aqueous solution: To investigate the potential rate controlling step such as the mass transfer or chemical reaction processes, pseudo-first order model, pseudo-second order model, Elovich model and Intraparticular diffusion model were tested on these experimental data.
The pseudo-first-order model is based on multilayer adsorption on the surface of each adsorbent material. This type of adsorption is based on van der Waal type interactions between tartrazine yellow and the different materials. These interactions thus demonstrate physical adsorption between the adsorbate and the adsorbent. Similarly, we also observe a good fit of the results with the pseudo second order model with the values of the coefficient of determination close to unity (R2>0.98) thus indicating chemical adsorption. This chemical adsorption is also supported with the adjustment of the Elovich model. The negative value of Qm obtained from the pseudo-second order model on the adsorption by the CC-H3PO4 material indicates that this model cannot be used to describe the results obtained. The negative values of the coefficient of determination obtained whatever the material (CC- HNO3 and CC-H3PO4) indicate that this model cannot be used to describe the process of adsorption on these biomaterials and the low value obtained for the material CC-H2O indicates that diffusion is not the limiting step of the adsorption phenomenon that takes place. It emerges from the rest of the models that there is a competition between physisorption and chemisorption for the adsorption of tartrazine yellow on these biomaterials studied (Figure 6 and Table 2).

Figure 6: Non-linear kinetic plot for tartrazine onto CC-H2O, CCHNO3 and CC-H3PO4. Note:  Qexp CC-H2O (mg/g),
Qexp CC-H2O (mg/g),  First order,
First order,  intraparticular diffusion.
intraparticular diffusion.
| N° | Models | Constants | Values | R2 | χ2 | RMSE | |
|---|---|---|---|---|---|---|---|
| CC-H2O | |||||||
| 1 | Pseudo first-order | Qe (mg/g) | 9.0065 | 0.9614 | 0.4619 | 1.7178 | |
| K1 (1/min) | 0.146 | ||||||
| 2 | Pseudo second order | Qe (mg/g) | 9.8992 | 0.9832 | 0.1672 | 1.116 | |
| K2 (g/min.mg) | 0.023 | ||||||
| 3 | Elovich | α (mg/g.min) | 17.5404 | 0.9275 | 0.1706 | 1.1946 | |
| β (g/mg) | 0.7079 | ||||||
| 4 | Intraparticular diffusion | Kp (mg/g.min0.5) | 0.8913 | 0.6825 | 1.2274 | 4.247 | |
| C (mg/g) | 2.8866 | ||||||
| CC-HNO3 | |||||||
| 1 | Pseudo first-order | Qe (mg/g) | 7.0057 | 0.9778 | 0.1396 | 0.989 | |
| K1 (1/min) | 0.7113 | ||||||
| 2 | Pseudo second order | Qe (mg/g) | 7.3216 | 0.9874 | 0.0811 | 0.7613 | |
| K2 (g/min.mg) | 0.2722 | ||||||
| 3 | Elovich | α (mg/g.min) | 31.15x107 | 0.926 | 0.0533 | 0.6148 | |
| β (g/mg) | 3.3758 | ||||||
| 4 | Intraparticular diffusion | Kp (mg/g.min0.5) | 0.566 | -0.0302 | 5.4438 | 4.8579 | |
| C (mg/g) | 3.5862 | ||||||
| CC-H3PO4 | |||||||
| 1 | Pseudo first-order | Qe (mg/g) | 8.4592 | 0.9923 | 0.058 | 0.7005 | |
| K1 (1/min) | 0.5649 | ||||||
| 2 | Pseudo second order | Qe (mg/g) | -8.6238 | 0.9951 | 0.0366 | 0.5577 | |
| K2 (g/min.mg) | 0.2466 | ||||||
| 3 | Elovich | α (mg/g.min) | 43.16x104 | 0.9271 | 0.0677 | 0.7397 | |
| β (g/mg) | 2.0235 | ||||||
| 4 | Intraparticular diffusion | Kp (mg/g.min0.5) | 0.6528 | -0.1065 | 6.517 | 5.8072 | |
| C (mg/g) | 4.3057 | ||||||
Table 2: Optimum kinetics parameters and their statistical comparison values onto CC-H2O, CC-HNO3 and CC-H3PO4.
Batch equilibrium experiments: The adsorption isotherm indicates how the adsorption molecules distribute between the liquid phase and the solid phase when the adsorption process reaches an equilibrium state. The analysis of the isotherm data by fitting them to different isotherm models is an important step to find the suitable model that can be used for design purpose. The study of the isotherms of adsorption is carried out on isotherms with two parameters and those of three well-known parameters [41].
1-isotherm with 2 parameters
For this work, 5 isothermal models namely Langmuir, Freundlich, Temkin and Dubinin-Raduskevich and Jovanovic were used, the plots are in Figure 7 and Table 3 presents the constants obtained, it appears that the Jovanovic model better describes the adsorption of the compound on the CC-H2O material with the highest value of the coefficient of determination R2=0.9912 and the lowest value of the Chi-test χ2 of 0.0325. This model is based on the assumptions contained in the model as that of Langmuir, but which gives the possibility of certain mechanisms between the adsorbent and the absorbate. This model is all the more confirmed as it is followed by the Langmuir model. For the CC-HNO3 material, the Dubinin- Radushkevich model better describes the adsorption. This model with its semi-empirical equation describes adsorption with a pore filling mechanism. This model also assumes multilayer adsorption involving Van der Waals forces, applicable to physical adsorption processes. For the CC-H3PO4 material, the Langmuir model best describes the adsorption phenomenon, followed by the Temkin model. The Temkin adsorption energies are all positive on the 3 materials, which implies exothermic adsorption. The adsorption energies of the Dubinin-Radushkevich model are: 16.222; 20.412; 19.612 kJ/mol respectively for CC-H2O, CC-HNO3, CC-H3PO4 materials. All these values above 16 kJ/mol imply that the process is dominated by intraparticle diffusion [42].

Figure 7: Non-linear isotherm plot for two-parameter models onto CC-H2O, CC-HNO3 and CC-H3PO4. Note:  Qexp CC-H2O (mg/g),
Qexp CC-H2O (mg/g),  First order,
First order,  intraparticular diffusion.
intraparticular diffusion.
| Models | Constants | Values | R2 | χ2 | RMSE |
|---|---|---|---|---|---|
| CC-H2O | |||||
| Langmuir | Qmax (mg.g-1) | 14.8864 | 0.9872 | 0.0478 | 0.4995 |
| KL (L.mg-1) | 0.0358 | ||||
| Freundlich | KF (L.mg-1) | 0.8761 | 0.9646 | 0.1474 | 0.8196 |
| n | 1.5521 | ||||
| Temkin | a (L.mg-1) | 0.3838 | 0.9837 | 0.0876 | 0.5780 |
| b (J.mol-1) | 804.1662 | ||||
| Dubinin-radushkevich | Qmax (mg.g-1) | 10.2413 | 0.9817 | 0.1669 | 0.6339 |
| K (L.mg-1) | 0.0019 | ||||
| Jovanovic | Qmax (mg.g-1) | 9.7460 | 0.9912 | 0.0325 | 0.4117 |
| KJ (L.mg-1) | -0.0516 | ||||
| CC-HNO3 | |||||
| Langmuir | Qmax (mg.g-1) | 10.4031 | 0.9353 | 0.2098 | 1.0003 |
| KL (L.mg-1) | 0.0953 | ||||
| Freundlich | KF (L.mg-1) | 1.7511 | 0.8215 | 0.5392 | 1.5988 |
| n | 2.2652 | ||||
| Temkin | a (L.mg-1) | 0.7142 | 0.9381 | 0.1833 | 1.0408 |
| b (J.mol-1) | 969.0134 | ||||
| Dubinin-radushkevich | Qmax (mg.g-1) | 9.2545 | 0.9760 | 0.0688 | 0.6547 |
| K (L.mg-1) | 0.0012 | ||||
| Jovanovic | Qmax (mg.g-1) | 7.9128 | 0.9685 | 0.1103 | 0.7059 |
| KJ (L.mg-1) | -0.1062 | ||||
| CC-H3PO4 | |||||
| Langmuir | Qmax (mg.g-1) | 11.9452 | 0.9974 | 0.0087 | 0.2241 |
| KL (L.mg-1) | 0.0656 | ||||
| Freundlich | KF (L.mg-1) | 1.3354 | 0.9844 | 0.0842 | 0.5362 |
| n | 1.8783 | ||||
| Temkin | a (L.mg-1) | 0.6132 | 0.9964 | 0.132 | 0.2638 |
| b (J.mol-1) | 920.8788 | ||||
| Dubinin-radushkevich | Qmax (mg.g-1) | 9.4449 | 0.9784 | 0.1127 | 0.6622 |
| K (L.mg-1) | 0.0013 | ||||
| Jovanovic | Qmax (mg.g-1) | 8.6267 | 0.9935 | 0.0230 | 0.3635 |
| KJ (L.mg-1) | -0.0798 | ||||
Table 3: Optimum isotherm parameters and their statistical comparison values for two-parameter models onto CC-H2O, CC-HNO3 and CC- H3PO4.
Three parameter adsorption models
The application of models with more than two parameters necessarily implies the use of nonlinear forms because it is almost impossible to obtain three unknowns from a straight line. For these studies of isotherms with three parameters, we have chosen five, namely the models of Redlich-Peterson, Sips, Toth, Hill and Khan. Figure 8 presents the plots obtained for the three materials and table Y gives the constants of these isotherms. Table 4 presents the calculated parameters of these five adsorption isotherms obtained using the nonlinear fit analysis. As indicated in Table 4, all the values of the coefficient of determination whatever the model are close to unity (R2>0.96) except the Hill model on the CC-HNO3 material which has a low value of the coefficient of determination R2=0.8706 and a large value of chi-square test χ2. The values of β and n obtained respectively from the Redlich-Peterson and Toth models are different from 1, which means that the adsorption of tartrazine yellow by these three materials cannot be reduced to the Langmuir isotherm. The very high R2 values (R2>0.96) obtained indicate the suitability of all these models for the adsorption of tartrazine yellow. These models thus highlight the existence of heterogeneous adsorption sites on the surface of these three materials. According to the work of Ho et al., the small values of χ2 and RMSE indicate a better adjustment of the model [42,43].

Figure 8: Non-linear isotherm plot for three-parameter models onto CC-H2O, CC-HNO3 and CC-H3PO4. Note:  Qexp CC-H2O (mg/g),
Qexp CC-H2O (mg/g),  intraparticular diffusion.
intraparticular diffusion.
| Models | Constants | Values | R2 | χ2 | RMSE | |
|---|---|---|---|---|---|---|
| CC-H2O | ||||||
| Redlich-peterson | A (L.g-1) | 12.7508 | 0.965 | 0.1454 | 0.8139 | |
| B (L.mg-1) | 13.7765 | |||||
| β | 0.3659 | |||||
| Sips | Ks (L.g-1) | 60.0972 | 0.969 | 0.1291 | 0.7611 | |
| as (L.g-1) | 0.0138 | |||||
| βs | 1.4294 | |||||
| Toth | Q (mg/g) | 0.9349 | 0.9657 | 0.1421 | 0.8058 | |
| Ke | 0.2006 | |||||
| n (mg/g) | 0.6088 | |||||
| Hill | Qm (mg/g) | 1.0476 | 0.9651 | 0.1452 | 0.8125 | |
| KH (L.g-1) | 0.2135 | |||||
| nH | 0.834 | |||||
| Khan | Qm (mg/g) | 4.9386 | 0.9793 | 0.08 | 0.6308 | |
| bk (L.g-1) | 0.1236 | |||||
| ak | 0.5548 | |||||
| CC-HNO3 | ||||||
| Redlich-peterson | A (L.g-1) | 0.6164 | 0.9985 | 0.0055 | 0.1685 | |
| B (L.mg-1) | 0.002 | |||||
| β | 1.9382 | |||||
| Sips | Ks (L.g-1) | 8.0184 | 0.987 | 0.0493 | 0.494 | |
| as (L.g-1) | 0.0332 | |||||
| βs | 0.5602 | |||||
| Toth | Q (mg/g) | 1.24x104 | 0.998 | 0.0072 | 0.1882 | |
| Ke | 385.3453 | |||||
| n (mg/g) | 1.6674 | |||||
| Hill | Qm (mg/g) | 2.2029 | 0.8706 | 0.3962 | 1.3728 | |
| KH (L.g-1) | 1.4384 | |||||
| nH | 1.813 | |||||
| Khan | Qm (mg/g) | 1.2x103 | 0.9907 | 0.0399 | 0.3918 | |
| bk (L.g-1) | 0.0006 | |||||
| ak | 63.7796 | |||||
| CC-H3PO4 | ||||||
| Redlich-peterson | A (L.g-1) | 0.8508 | 0.9977 | 0.0098 | 0.2104 | |
| B (L.mg-1) | 0.097 | |||||
| β | 0.919 | |||||
| Sips | Ks (L.g-1) | 12.4529 | 0.9975 | 0.0096 | 0.2203 | |
| as (L.g-1) | 0.0664 | |||||
| βs | 1.0381 | |||||
| Toth | Q (mg/g) | 9.7124 | 0.9976 | 0.0088 | 0.2141 | |
| Ke | 12.7772 | |||||
| n (mg/g) | 0.975 | |||||
| Hill | Qm (mg.g-1) | 1.6518 | 0.9947 | 0.0305 | 0.3145 | |
| KH (L.g-1) | 1.5125 | |||||
| nH | 1.9819 | |||||
| Khan | Qm (mg/g) | 8.3125 | 0.9978 | 0.0097 | 0.2039 | |
| bk (L.g-1) | 0.1009 | |||||
| ak | 0.8258 | |||||
Table 4: Optimum isotherm parameters and their statistical comparison values for three-parameter models onto CC-H2O, CC-HNO3 and CC- H3PO4.
Conclusion
The present work shows that the quantity of Tartrazine dye adsorbed varied with initial solution pH, biomass dosage, dye concentration and time of contact. The biosorption process achieved better results with the washed cocoa shell (CC-H2O). Nonlinear regression analysis showed the best fit for pseudo second order kinetics regardless of material with Chi-square (χ2) test values of 0.1672, 0.0811 and 0.0366 respectively for CC-H2O, CC-HNO3 and CC-H3PO4. Equilibrium data were fitted to two-parameter mono-solute models and mono-solute three-parameter models. Adsorption isotherm data were best described by Jovanovic model for water washed substrate, Langmuir model for phosphoric acid treated substrate and Dubinin-Radushkevich model for treated substrate to nitric acid for the 2-parameter isotherms. The results indicated cocoa shell constitutes a promising low-cost technology biosorbent for the removal of waste dyes.
Declaration of Interests
The authors declare that there are no conflicts of interest.
Acknowledgements
We appreciate the technical assistance of the Researchers of Material and Process Engineering Team (MPET)/RU-NOCHEE of the Department of Chemistry, University of Dschang, Cameroon.
References
- Zaviska F, Patrick D, Guy M, Jean-Francois B. modelisation du traitement de micropolluants organiques par oxydation electrochimique. J Water Sci. (2009); 535.
- Chatterjee S, Lee MW, Woo SH. Adsorption of congo red by chitosan hydrogel beads impregnated with carbon nanotubes. Bioresour Technol. 2010;101(6):1800-1806.
[Crossref] [Google Scholar] [PubMed]
- Daneshvar N, Rasoulifard MH, Khataee AR, Hosseinzadeh F. Removal of CI Acid Orange 7 from aqueous solution by UV irradiation in the presence of ZnO nanopowder. J Hazard Mater. 2007;143(1-2):95-101.
[Crossref] [Google Scholar] [PubMed]
- Modirshahla N, Behnajady MA, Kooshaiian S. Investigation of the effect of different electrode connections on the removal efficiency of Tartrazine from aqueous solutions by electrocoagulation. Dyes Pigm. 2007;74(2):249-257.
- Nanganoa LT, Ketcha JM, Ndi JN. Kinetic and equilibrium modeling of the adsorption of amaranth from aqueous solution onto smectite clay. Res J Chem Sci. 2014;2231:606X.
- Al-Sultani Kadhim F, Al-Seroury FA. Characterization the removal of phenol from aqueous solution in fluidized bed column by rice husk adsorbent. Res J Recent Sci. 2012;2277:2502.
- Kumar A, Rao NN, Kaul SN. Alkali-treated straw and insoluble straw xanthate as low cost adsorbents for heavy metal removal–preparation, characterization and application. Bioresour Technol. 2000;71(2):133-142.
- Nigam P, Armour G, Banat IM, Singh D, Marchant R. Physical removal of textile dyes from effluents and solid-state fermentation of dye-adsorbed agricultural residues. Bioresour Technol. 2000;72(3):219-226.
- Tchuifon DR, Ndifor-Angwafor GN, Bopda A, Anagho SG. Modeling of phenol adsorption isotherm onto activated carbon by non-linear regression methods: models with three and four parameters. Desalin Water Treat. 2018;136:199-206.
- Kumar KV, Porkodi K. Batch adsorber design for different solution volume/adsorbent mass ratios using the experimental equilibrium data with fixed solution volume/adsorbent mass ratio of malachite green onto orange peel. Dyes Pigm. 2007;74(3):590-594.
- Kumar KV, Sivanesan S. Isotherm parameters for basic dyes onto activated carbon: Comparison of linear and non-linear method. J Hazard Mater. 2006;129(1-3):147-150.
[Crossref] [Google Scholar] [PubMed]
- Subramanyam B, Das A. Linearized and non-linearized isotherm models comparative study on adsorption of aqueous phenol solution in soil. Int J Environ Sci. 2009;6(4):633-640.
- Krishni RR, Foo KY, Hameed BH. Adsorption of methylene blue onto papaya leaves: comparison of linear and nonlinear isotherm analysis. Desalin Water Treat. 2014;52(34-36):6712-6719.
- Brdar M, Sciban M, Takaci A, Dosenovic T. Comparison of two and three parameters adsorption isotherm for Cr (VI) onto Kraft lignin. J Chem Eng. 2012;183:108-111.
[Crossref] [Google Scholar] [PubMed]
- Pasalari H, Ghaffari HR, Mahvi AH, Pourshabanian M, Azari A. Activated carbon derived from date stone as natural adsorbent for phenol removal from aqueous solution. Desalin Water Treat. 2017;72:406-417.
- Subramanyam B, Das A. Linearised and non-linearised isotherm models optimization analysis by error functions and statistical means. J Environ Health Sci Eng. 2014;12(1):1-6.
[Crossref] [Google Scholar] [PubMed]
- Shahmohammadi-Kalalagh S, Babazadeh H. Isotherms for the sorption of zinc and copper onto kaolinite: comparison of various error functions. Int J Environ Sci Technol. 2014;11(1):111-118.
- Bera A, Kumar T, Ojha K, Mandal A. Adsorption of surfactants on sand surface in enhanced oil recovery: Isotherms, kinetics and thermodynamic studies. Appl Surf Sci. 2013;284:87-99.
- Tchuifon DR, Anagho SG, Njanja E, Ghogomu JN, Ndifor-Angwafor NG, Kamgaing T. Equilibrium and kinetic modelling of methyl orange adsorption from aqueous solution using rice husk and egussi peeling. Int J Chem Sci. 2014;12(3):741-761.
- L’elimination des micropolluants dans les eaux residuaires urbaines. Projet. Ecole.
- Polytechnique Federale de Lusanne. Lusanne. Suisse.
- Ndi NJ, Ketcha MJ, Anagho GS, Ghogomu NJ, Belibi EP. Physical and chemical characteristics of activated carbon prepared by pyrolysis of chemically treated cola nut (cola acuminata) shells wastes and its ability to adsorb organics. Int J Chem Technol. 2014;3(1):1-3.
- Kuete IH, Tchuifon DR, Ndifor-Angwafor GN, Kamdem AT, Anagho SG. Kinetic, isotherm and thermodynamic studies of the adsorption of thymol blue onto powdered activated carbons from Garcinia cola nut shells impregnated with H3PO4 and KOH: non-linear regression analysis. Journal of Encapsulation and Adsorption Sciences. 2020;10(1):1-27.
- Tiotsop Kuete IH, Tchuifon Tchuifon RD, Bopda A, Sadeu Ngakou C, Nche GN, Gabche Anagho S. Adsorption of Indigo Carmine onto Chemically Activated Carbons Derived from the Cameroonian Agricultural Waste Garcinia cola Nut Shells and Desorption Studies. J Chem. 2022.
- Chien SH, Clayton WR. Application of Elovich equation to the kinetics of phosphate release and sorption in soils. Soil Sci Soc Am J. 1980;44(2):265-268.
- Axtell NR, Sternberg SP, Claussen K. Lead and nickel removal using Microspora and Lemna minor. Bioresour Technol. 2003;89(1):41-48.
- S. K. Knaebel. Adsorbent selection. Int j trend res Dev. 2004.
- Ayawei N, Ebelegi AN, Wankasi D. Modelling and interpretation of adsorption isotherms. J Chem. 2017.
- Behbahani TJ, Behbahani ZJ. A new study on asphaltene adsorption in porous media. Pet Coal. 2014;56(5):459-466.
- Redlich OJ, Peterson DL. A useful adsorption isotherm. J Phys Chem. 1959;63(6):1024.
- Sips R. On the structure of a catalyst surface. J Chem Phys. 1948;16(5):490-495.
- Toth J. State equation of the solid-gas interface layers. Acta Chim Hung. 1971;69:311-328.
- Farouq R, Yousef NS. Equilibrium and kinetics studies of adsorption of copper (II) ions on natural biosorbent. Int J Chem En App. 2015;6(5):319.
- Ringot D, Lerzy B, Chaplain K, Bonhoure JP, Auclair E, Larondelle Y. In vitro biosorption of ochratoxin A on the yeast industry by-products: comparison of isotherm models. Bioresour Technol. 2007;98(9):1812-1821.
[Crossref] [Google Scholar] [PubMed]
- Khan AR, Ataullah R, Al-Haddad A. Equilibrium adsorption studies of some aromatic pollutants from dilute aqueous solutions on activated carbon at different temperatures. J Colloid Interface Sci. 1997;194(1):154-165.
[Crossref] [Google Scholar] [PubMed]
- El-Khaiary MI. Least-squares regression of adsorption equilibrium data: comparing the options. J Hazard Mater. 2008;158(1):73-87.
[Crossref] [Google Scholar] [PubMed]
- Hao OJ, Kim H, Chiang PC. Decolorization of wastewater. Crit Rev Environ Sci. 2000;30(4):449-505.
- Hossain MA, Ngo HH, Guo WS, Setiadi T. Adsorption and desorption of copper (II) ions onto garden grass. Bioresour Technol. 2012;121:386-395.
[Crossref] [Google Scholar] [PubMed]
- Vinoth M, Lim HY, Xavier R, Marimuthu K, Sreeramanan S, Rosemal HM, et al. Removal of methyl orange from solutions using yam leaf fibers. Int J Chem Tech Res. 2010;2(4):1892-1900.
- Aravindhan R, Rao JR, Nair BU. Removal of basic yellow dye from aqueous solution by sorption on green alga Caulerpa scalpelliformis. J Hazard Mater. 2007;142(1-2):68-76.
[Crossref] [Google Scholar] [PubMed]
- Langmuir I. The constitution and fundamental properties of solids and liquids. Part I. Solids. J Am Chem Soc. 1916;38(11):2221-2295.
- Vijayaraghavan K, Padmesh TV, Palanivelu K, Velan M. Biosorption of nickel (II) ions onto Sargassum wightii: application of two-parameter and three-parameter isotherm models. J Hazard Mater. 2006;133(1-3):304-308.
[Crossref] [Google Scholar] [PubMed]
- Ho YS, Porter JF, McKay G. Equilibrium isotherm studies for the sorption of divalent metal ions onto peat: copper, nickel and lead single component systems. Water Air Soil Pollut. 2002;141(1):1-33.
Citation: Nemgne MN, Kouteu APN, Tchuifon DRT, Ngakou CS, Nche NAG, Gabche AS (2022) Modeling of Tartrazine Dye Adsorption onto Treated and Untreated Cocoa Shell by Non-Linear Regression Methods. Modern Chem Appl. 10:383.
Copyright: © 2022 Nemgne MN, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.