Journal of Nanomedicine & Nanotechnology

Micromagnetic Manipulators - Ferromagnetic Microwire Systems for Diffusion and Separation of Para and Dia- magnetic Particles in Gradient Magnetic Field

Beklemisheva AV^1,2*, Gurevich AA^1,2, Panina LV^1,3, Suetina IA⁴, Mezentseva MV⁴, Zolotoreva MG⁵ and Beklemishev VN^{5 1}National University of Science and Technology (NUST MISIS), Moscow, 119040, Russia
²Institute for Design Problems in Microelectronics RAS, Moscow, 124365, Russia
³Immanuel Kant Baltic Federal University, Kaliningrad, 236004, Russia
⁴N. F. Gamaleya Federal Research Center for Epidemiology & Microbiology, Moscow, 123098, Russia
⁵National Research Nuclear University MEPhI, Moscow, 115409, Russia
^*Correspondence: Beklemisheva AV, National University of Science and Technology (NUST MISIS), Moscow, 119040, Russia, Tel: 74992302409, Email:

Received: 03-Nov-2020 Published: 30-Nov-2020, DOI: 10.35248/2157-7439.20.11.554

Introduction

Magnetism is a broad scientific field and magnetic materials have found a variety of practical applications. One area of exploring magnetic fields is micron-sized magnetic manipulators of biological objects having weak magnetic properties or marked with magnetic nanoparticles [1-8]. Micromagnet devices typically generate magnetic fields with strong spatial gradient to control particlesdynamics. Such fields are formed due to the selection of the composition of ferromagnetic substance in conjunction with the magnet geometry and its micron dimensions. Customarily, arrays of micromagnets on substrates produced by lithography or heavy ion etching are used in these applications [2,9-10]. In another approach, micromagnetic manipulators are made of magnetic or conducting rods and cylinders of length much larger than the radius [11-14]. The stray magnetic fields produced by micron-sized magnetic poles with gradients as high as kT/m are sufficient to impose on magnetic particles the forces which can surpass the other forces such as due to gravity, viscosity, thermal fluctuations. The use of thin conducting wires or stripes for generating a magnetic field is potentially interesting since this makes it possible to create adjustable field distributions in space and time by controlling the electric current in an individual element. The arrays of micron-sized conducting elements fabricated with electron-beam lithography were applied to manipulate some biological objects, e.g. magnetotactic bacteria [15]. However, this approach has a number of limitations including heat generation and restricted field gradients. In this paper we demonstrate a very flexible use of ferromagnetic microwires in thiazolamorphous state for para and dia-magnetic objects manipulation. Such microwires can be formed into different magnetic matrices and have different directions of magnetization in accordance with the experimental needs. Individual magnetized wires with localized magnetic poles can be used as magnetic tweezers [16].

Amorphous microwires are attractive as they have a tunable magnetic structure due to absence of the magnetocrystalline anisotropy [17]. The wires produced by Taylor − Ulitovsky method are covered by glass which is demonstrated to have biocompatibility. The wire diameter and glass thickness can be varied in a wide range 1-40 microns, 1-10 microns, respectively. We propose a number of concepts for manipulation by para and dia-magnetic objects with the use of microwires. A single microwire with an axial magnetization is a source of highly localized magnetic field and is capable of capturing even weakly paramagnetic particles. This could be of interest for force regulating in individual cells [18]. The arrays of wires with the magnetization along a diameter are suitable for enhancing paramagnetic particle diffusion. The pair of such wires closely spaced operate as a diamagnetic trap [19-26]. Finally, the wires with circular domain structure constitute periodic potential profile forparamagnetic particles. Applying a very small current and moving the domain walls creates a travelling wave potential, that is, typical magnetic ratchet [27],which controllably transports the particles.

Methods and Materials

Materials

The wires with fine surface morphology can be produced by Taylor-Ulitovsky method [22] in a glass shell as shown in Figure 1. The latter could also provide a protective and biocompatible layer. The size of the magnetic core of microwires varies in the range from 5 to 40 microns, and the thickness of the glass shell is within 1-10 microns. Typical hysteresis loops for the two types of wires are shown in Figure 2. When magnetized in a field along the axis, Fe-based amorphous microwires with an axial magnetic anisotropy are characterized by a rectangular hysteresis with reentrant magnetization jump (so called, large Barkhausen jump) [26]. The coercivity is lower than 50 A/m. Co-based wires have a circular anisotropy and demonstrate flat hysteresis with very small coercivity and remanence magnetization [L6]. The anisotropy field is also quite small of about 200 A/m. When magnetized by the field directed perpendicular to the axis, the curves do not show hysteresis. Quite strong fields are required for reaching the saturation value M_s, however, the Fe-based wires with higher M_s may have large perpendicular component of about 5 105 A/m (as M_s for Co-based alloys) at relatively small magnetizing field of 0.1 T.

Figure 1: Microwire in a cut, the boundary between ferromagnetic core and glass sheath is observable.

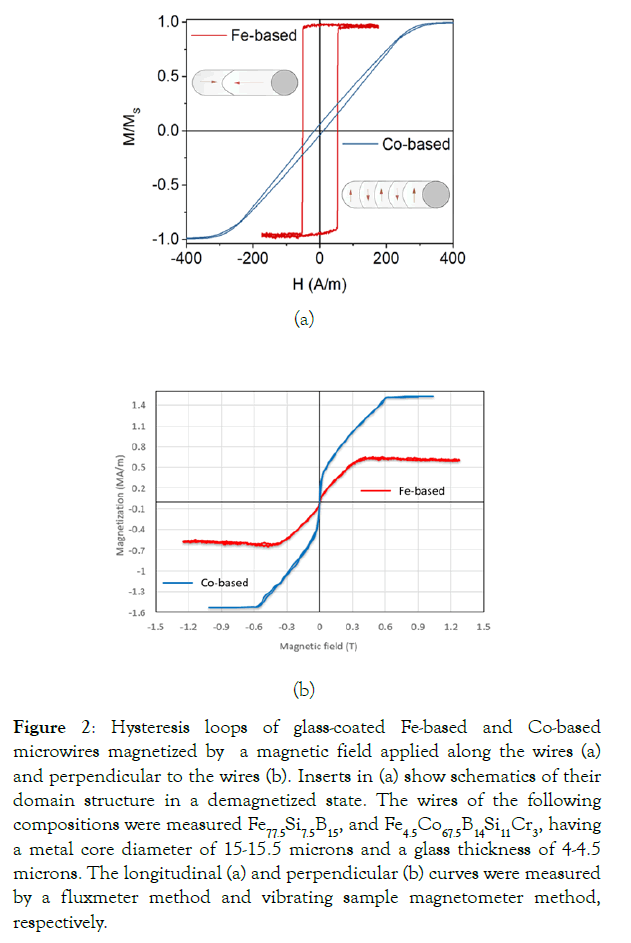
Figure 2: Hysteresis loops of glass-coated Fe-based and Co-based microwires magnetized by a magnetic field applied along the wires (a) and perpendicular to the wires (b). Inserts in (a) show schematics of their domain structure in a demagnetized state. The wires of the following compositions were measured Fe_77.5Si_7.5B₁₅, and Fe_4.5Co_67.5B₁₄Si₁₁Cr₃, having a metal core diameter of 15-15.5 microns and a glass thickness of 4-4.5 microns. The longitudinal (a) and perpendicular (b) curves were measured by a fluxmeter method and vibrating sample magnetometer method, respectively.

Biocompatibility of glass shell and effects of wire magnetizationon living cells

Since arrays of ferromagnetic microwires are supposed to be used in the experiments with living cells, an important issue is the influence of a high-gradient magnetic field on the vital activity of cells. The other issue is biocompatibility of the glass shell. To study the effect of a strong magneticfield on cells and biocompatibility of the glass shell (made of borosilicate) of microwires, a number of experiments was carried out. Microwires under the influence of a strong magnetic field, were in the cell suspension up to 3 days.

For the experiments, a continuous culture of normal cells of human embryonic fibroblasts (HEF) was selected from the collection of cell cultures. For culturing the cells, we used a standard Eagle MEM nutrient environment (Bio, Russia) with 10% Fetal Bovine Serum (Gibco®, USA). [19,20]. The microwire samples were sterilized with alcohol and ultraviolet light. For the MTT test, cells were plated on a 6-well panel at a concentration of 200 thousand cells per milliliter in each well in a volume of 2 ml of culture environment with 10% FBS and incubated in a CO₂- incubator with 5% CO₂ at 37°C. 72 hours after planting the formation of a subconfluent monolayer of cellsoccurred. Intact cells cultured in parallel with experimental ones served as control. The color intensity in the wells of the panel with control cells was taken as 100% viability.

After incubation of cells with these preparations for 72 hours in a CO₂ thermostat at 37°C, the culture medium was aspirated from the wells, 2 ml of medium with 400 μl MTT (3 [4,5-dimethyl-thiazol-2-yl] -2.5- diphenyltetrazolium, Sigma) at an initial concentration of 5 mg /ml and incubated for 4 hours. Then the medium with MTT was removed and 1 milliliter of dimethyl sulfoxide (DMSO) was added to dissolve the formed formazan crystals. The cell pellet was resuspended by pipetting for 5 min. Cell viability was assessed by the color intensity of the blue formazan solution by measuring the optical density at a wavelength of 545 nm using an Immunochem 2100 photometer (USA).

The MTT test results were assessed by comparing the optical density in the experimental and control wells. The percentage of viable cells was calculated as the ratio of the optical density of the treated cells and control cells. Statistical processing of the results was carried out using the software Microsoft Excel, "Statistica 6.0". The significance of the difference in mean values was established using the Student's t-test at a significance level of ≤ 0.01.

Visual control of changes in cell morphology during incubation with a microwire sample was done with a fluorescent microscope. The cells were grown on sterile cover slips in 6-well panels, stained with ethidium bromide by adding it to the culture medium, incubated for 15 min in a CO₂- incubator with 5% CO₂ at 37°C as shown in Figure 3.

Figure 3: Glass-coated microwire in a glass shell (16 microns in total diameter, glass thickness of 3 microns) in cell.suspension composed of cryoprotective environment (70%), Fetal Bovine Serum (20%), glycerine (10%). Exposure time was 24 hours. Right and left panels are for different magnification.

Theoretical approach

A particle with a magnetic dipole moment, p_m, placed in a magnetic field H has a potential energy:

     (1)

µ₀ is the permeability of vacuum. The magnetic particle may be characterized by a linear susceptibility: p_m = χVH, V is the particle volume. Then

     (2)

A single magnetic-dipole dynamics in solution when neglecting diffusion is described by the balance of fields including the Stokes force in viscous medium. If other forces are insignificant the balance equation is of the form

     (3)

When investigating small-scale systems, thermal noise may play a deciding role. The interaction of particle (p_m) with the environment is described by:

     (4)

The right-hand terms are related to the energy dissipation including viscous friction and randomly -fluctuating forces due to thermal noise ξ (t) obeying to the fluctuation–dissipation relation

Where k_B is the Boltzmann constant, T is the temperature, 2ηk_BT is the noise strength, and δ(t) is the Dirac delta function. When considering a statistical ensemble of magnetic dipoles with the probability density c(r,t) and combining the diffusion equation (when ∇U = 0) together with the Liouville-equation (ξ(t) = 0) the Fokker-Planck equation becomes of the form [28]:

      (5)

With the diffusion coefficient

     (6)

This also corresponds to the probability current (particle flow)

     (7)

which obeys the continuity equation:

     (8)

The diffusion of magnetic particles in the presence of gradient magnetic field forces follows Eq. (5) with specific initial and boundary condition. The change in c(r,t) eventually reaches the stationary distribution which corresponds to zero flow

J(r,t) = 0        (9)

First-order differential equation in (7) is solved with the condition of particle conservation in a restricted area.

Structure

The magnetic field H is produced by the wire magnetization. There small cross section ensures spatial distribution of H with high gradients in the range of 60 kT/m for wires of 10μm radius with magnetization of 5 105 A/m (as for Co-based alloys). We will consider three types of the wire magnetization as depicted in Figure 4 axial magnetization, (b) magnetization along diameter, and circular magnetization with the bamboo domain structure (c). In the case of uniformly magnetized wires, the stray fields are calculated exactly within an analytical approach [28-31]. In the presence of the circular domain structure, the stray field is generated at the domain wall (DW) location where the magnetization is directed perpendicular to the wire surface. In this case we will be interested in the paramagnetic particle trap by the DW due to local minima of the periodic magnetic potential. Applying a very small current of few mA, the DW can be moved and the effective potential experienced by the particle is travelling along the wire axis (z-axis) with the velocity u:

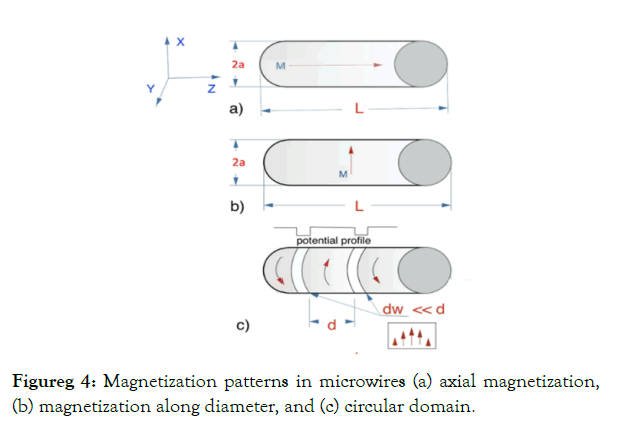
Figureg 4: Magnetization patterns in microwires (a) axial magnetization, (b) magnetization along diameter, and (c) circular domain.

U(r,t) = U(r - ut)

For a current of frequency the velocity is estimated as u = 2df, d is the domain width. When DW are displaced, the potential period 2d remains the same. Therefore, a wire with circular domains driven by a current represents a ratchet system making it possible to realize directed transport of paramagnetic particles along the wire. The average velocity along the wire in the steady state is of the form[28]

     (10)

Results and Discussions

Biocompatibility of microwires

Microwire cytotoxicity assay involves visual observation of cell proliferation in the microwire area as shown in Figures 3 & 5. This follows by MTT analysis and cell counting. It was observed that after exposure time of 72 hours, mostly living cells were observed, the cell count in the area of microwireswas1,87 · 10⁵, which is slightly higher than without microwires- 1,74 · 10⁵. The statistical distribution is shown in Figure 6. The number of cells was also estimated by optical intensity density for a wavelength of 545 nm. The relative parameter (figure of merit) was 0.863 in the microwire presence against 0.848 in the absence of microwires. Therefore, our results show a high survival rate of cell cultures in the area of microwire, which indicates their non-toxicity and biocompatibility and opens up the prospects of using microwires in biomedicine.

Figure 5: Cell suspension composed of cryoprotective environment (70%), Fetal Bovine Serum (20%), glycerine ( 10%) without the microwire sample in (a) and with the sample in (b). Exposure time was 72 hours.

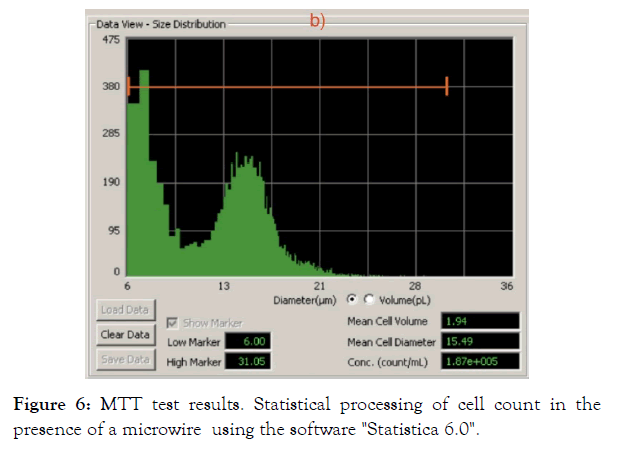
Figure 6: MTT test results. Statistical processing of cell count in the presence of a microwire using the software "Statistica 6.0".

Effects of the wire stray fields

The longitudinal magnetization of microwires (Figure 4a) can be used when the micromagnetic manipulator is configured like magnetic tweezers. In this case we modelled an individual paramagnetic particle behavior which is found in the vicinity of amicrowire with an axial magnetization. It is accelerated towards the tip and the velocity is estimated from equation (3). For a spherical particle, the viscous friction coefficient = 6πRη_s, where R is the particle radius and η_s is the solution viscosity. The velocity distribution is shown in Figure 7.

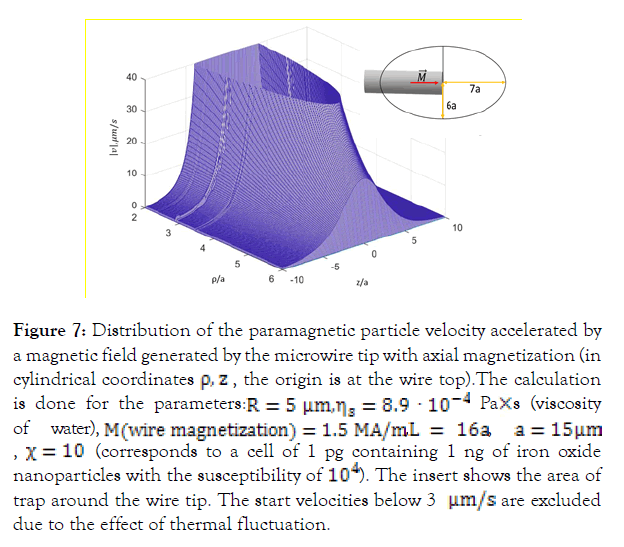
Figure 7: Distribution of the paramagnetic particle velocity accelerated by a magnetic field generated by the microwire tip with axial magnetization (in cylindrical coordinates ρ,z, the origin is at the wire top).The calculation is done for the parameters: R = 5µm, η_s = 8.9 · 10^-4 Pa×s (viscosity of water), M(wire Magnetization) = 1.5 MA/m,L = 16a, a = 15µm, χ = 10 (corresponds to a cell of 1 pg containing 1 ng of iron oxide nanoparticles with the susceptibility of 10⁴). The insert shows the area of trap around the wire tip. The start velocities below 3 μm/s are excluded due to the effect of thermal fluctuation.

The wires with the magnetization along the diameter (Figure 4b) may create quite large areas for capturing magnetic nanoparticles. In this case it is reasonable to consider the paramagnetic particle diffusion in the presence of the wire stray magnetic fields. In the case of long microwires the energy U(r) which is defined by H² (eq. (2)) depends only on polar coordinate r and diffusion equation (5) becomes one-dimensional.The diffusion of even weakly paramagnetic particles quickly proceeds towards the wire surface as shown in Figure 7. For the parameters used, the concentration increases by 2.5 times after 30 s, whilst the stationary distribution (eq. (9)) gives 3.5 magnifications.

A pair of finite length and very closely spaced microwires with perpendicular magnetization may represent a trap for diamagnetic particles with the susceptibility as small as that of water (-10^-5) In this case the energy profile is characterized by two-dimensional minimum (along z and x directions, M is along x) situated between the wires as shown in Figures 8 and 9.

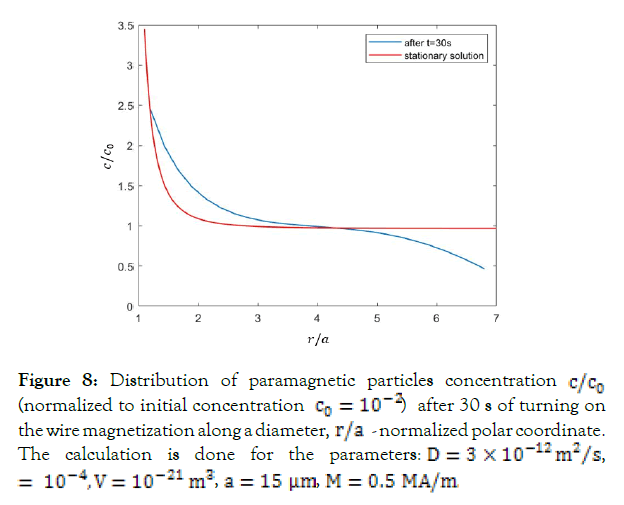
Figure 8: Distribution of paramagnetic particles concentration c/c₀ (normalized to initial concentration c₀ = 10^-2) after 30 s of turning on the wire magnetization along a diameter, r/a - normalized polar coordinate. The calculation is done for the parameters: D = 3 × 10^-12 m²/s, = 10^-4, V = 10^-21 m³, a = 15 µm, M = 0.5 MA/m.

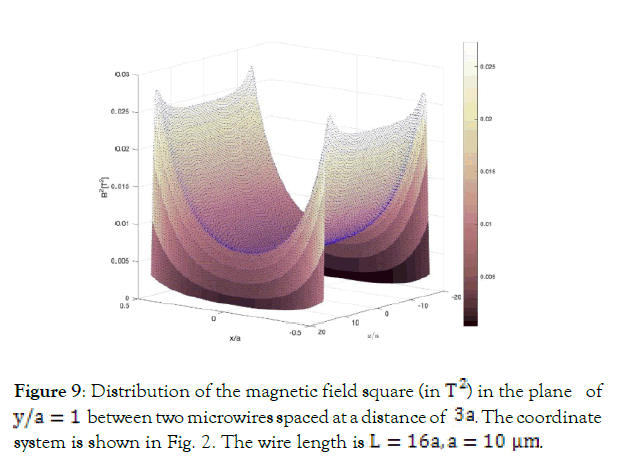
Figure 9: Distribution of the magnetic field square (in T²) in the plane of y/a = 1 between two microwires spaced at a distance of 3a. The coordinate system is shown in Fig. 2. The wire length is L = 16a, a = 10µm.

This potential may be sufficient to overcome gravity and realize the cell levitation. The wire-pairs must be located in horizontal plane (x, z) and y -axis is vertical. The total energy density is of the form:

     (11)

In (11), g is the gravitational acceleration and m_p is the particle mass.Stable 3D-minimum is realized at heights for and particle mass density of that of water. It increases with increasing the absolute value of the susceptibly. Thus, for the parameter used (as for Figure 8) the levitation height increases from 8.5 μm for χ = -10^-5 to 9.7µm for χ = -10^-4, Therefore, the particle size for levitation above the microwires should be much smaller than the wire radius.

The arrays of perpendicularly magnetized microwires situated in the plane (x,z) with small distance between them can be used for cell levitation. Each two neighboring wires along x-direction fulfill the condition of a diamagnetic trap. The spatial distribution of the total energy U_t is convenient to represent by equipotential curves in the plane x=0 as shown in Figures 9 & 10. To magnetize the wires along a diameter an external magnetic field H_ex is needed. This uniform field adds to the magnetic potential gradient and helps to slightly increase the levitation height.

Circular domains in Co-based microwires (as in Figure 4c) can be displaced by a circumferential magnetic field generated by a smallac current. This system is of considerable interest since the magnetic potential created by the stray field at the DW location is periodic and asymmetrical due to the wall displacements. This is a so-called ratchet potential. The current drives the system permanently out of equilibrium. The estimated average velocity given by Eq.(10) along the wire in the steady state depends on the driving current frequency and parameters of the domain structure. For paramagnetic particles with parameters as for Figure 7, optimal frequencies of 1-2 Hz and domain length of 10 μm the average velocity is about 8-12 μm/s. However, this case requires additional instigations as the drift velocity strongly depends on the DW structure parameters.

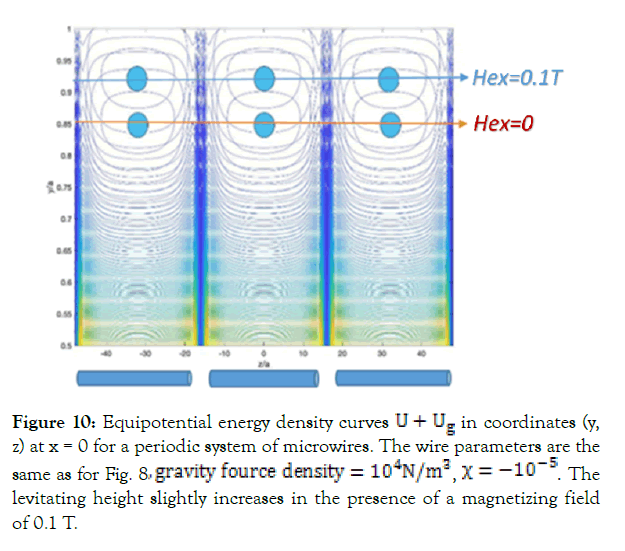
Figure 10: Equipotential energy density curves U + U_g in coordinates (y, z) at x = 0 for a periodic system of microwires. The wire parameters are the same as for Fig. 8, gravity fource density = 10⁴N/m³, χ = -10^-5. The levitating height slightly increases in the presence of a magnetizing field of 0.1 T.

Conclusion

The considered system of microwires has the prospect of applications in the field of bio-objects manipulation. We proposed and modelled three basic concepts of microwire use as a source of localized magnetic fields: a few number of individual wires with bi-stable magnetization reversal acting as magnetic tweezers, arrays of perpendicular magnetized wires for enhancing paramagnetic particles diffusion and levitating diamagnetic cells, and wires with circular domain structure for controlling paramagnetic particles transport along the wires. Development in the field of application for the localization.

Acknowledgment

This work was supported by the Russian Foundation for Basic Research (RFBR 19-32-90263/19) and by Ministry of Science and Higher Education of the Russian Federation in the framework of the State Task (project code 0718-2020-0037).

REFERENCES

1. Brehm-stecher BF, Johnson EA. Single-cell microbiology: tools, technologies, and applications. Microbiol Mol Biol Rev. 2004; 68: 538-561.
2. Zablotskii V, Dejneka A, Dempsey NM. Life on Magnets: Stem Cell Networking on Micro-Magnet Arrays. PLoS ONE. 2013; 8: 70416.
3. Zablotskii V, Lunov O, Kubinova S. Effects of high-gradient magnetic fields on living cell machinery. J Physics D: Applied Physics. 2016; 49: 493003.
4. Zablotskii V, Zoe W, Dejneka A. Modulation of monocytic leukemia cell function and survival by high gradient magnetic fields and mathematical modeling studies. Biomaterials. 2014; 35: 3164-3171.
5. Zablotskii V, Polyakova T. How a High-Gradient Magnetic Field Could Affect Cell Life. Sci Re P. 2016; 37: 407-412.
6. Yu X, He R, Li S. Magneto-Controllable Capture and Release of Cancer Cells by Using a Micropillar Device Decorated with Graphite Oxide-Coated Magnetic Nanoparticles. Small. 2013; 9(22): 3895–3901.
7. Wang H, Zhang X. Magnetic Fields and Reactive Oxygen Species. Int J Mol Sci. 2017; 2175: 18.
8. Liascukiene I, Amselem G. Capture of colloidal particles by a moving microfluidic bubble. 2018; 992-1000.
9. Kauffmann P, Dempsey NM. Diamagnetically trapped arrays of living cells above micromagnets. Lab Chi P. 2011;11: 3153.
10. Pivetal J, Royet D, Ciuta G. Micro-magnet arrays for specific single bacterial cell positioning. J Magnetism Magnetic Mat. 2015; 380: 72-77.
11. Blums E, Plavins J, Chukhrov A. High-gradient magnetic separation of magnetic colloids and suspensions. J Magnetism Magnetic Materials. 1983; 39: 147-151.
12. Lawson WF, Simons WH, Treat RP. The dynamics of a particle attracted by a magnetized wire. J Appl Phy. 1977; 48: 3213.
13. Melyanchik O. Ferromagnetic glass-coated microwires for cell manipulation. J Magn Magn Mat. 2020; 512: 166991.
14. Melyanchik O. Design of conductive microwire systems for manipulation of biological cells. IEEE Transaction on Magnetics. 2018; 54: 5400405.
15. Lee H, Purdon AM, Westervelt RM. Manipulation of biological cells using a microelectromagnet matrix. Appl Phys Lett. 2004; 85(6): 1063–1065.
16. Tanase M, Biais N, Sheetz M. Magnetic Tweezers in Cell Biology. Methods Cell Biol. 2007; 83: 473-493.
17. Vázquez M, Chiriac H, Zhukov A, Panina L. On the state-of-the-art in magnetic microwires and expected trends for scientific and technological studies. Phys Status Solid Appl Mater Sci. 2011.
18. Kollmannsberger P, Fabry B. High-force magnetic tweezers with force feedback for biological application. Rev Sci Instrum 2007.
19. Podchernyaeva R, Suetina IA, Lopatina OA, Ostroumov SA. Evaluation of the toxicity of nanoparticles of copper and iron oxides on cell culture: analysis of histograms obtained by an automatic cell counter SCEPTER. “Nanomaterials and nanotechnology in living systems. Safety and nanomedicine ". Moscow: RUSNANO 2011;91-92.
20. Podchernyaeva RYa, Suetina IA, Mikhailova GR.Cultivation of transplanted cell lines on carbon nanotube substrates and the effect of electrical stimulation on cell proliferation. Questions of Virology. 2012; 57(5): 46.
21. Chiriac H, Corodeanu S, Lostun M, Stoian G, Ababei G, Ovari TA. Rapidly solidified amorphous nanowires. J Appl Phys. 2011;109(6): 063902.
22. Baranov SA, Larin VS, Torcunov AV. Technology, preparation and properties of the cast glass-coated magnetic microwires. Crystals. 2017; 7(6): 136.
23. Gunawan O, Virgus Y, Fai K. A parallel dipole line system. Applied Physics Letters. 2015; 106: 062407.
24. Beklemisheva AV, Yudanov NA, Gurevich AA, Panina LV, Zablotskiy VA, Deyneka A, et al. Matrices of Ferromagnetic Microwires for the Control of Cellular Dynamics and Localized Delivery of Medicines. Phys Met Metallogr. 2019; 120(6): 556-562.
25. Gurevich AV, Beklemisheva E, Levada V, Rodionova LV. Panina Ferromagnetic Microwire Systems as a High-Gradient Magnetic Field Source for Magnetophoresis. IEEE Magn Lett. 2020; 11: 1.
26. Corte-Leon P, Gonzalez-Legarreta L, Zhukova V, Ipatov M, Blanco JM, Churyukanova M, et al. Controlling the domain wall dynamics in Fe-, Ni- and Co-based magnetic microwires. J Alloy Compd. 2020.
27. Stoop RL, Arthur V. Straube, PietroTierno Enhancing Nanoparticle Diffusion on a Unidirectional Domain Wall Magnetic Ratchet. Nano Lett. 2019; 19(1): 433–440.
28. Reimann P. Brownian motors: noisy transport far from equilibrium. Physics Reports. 2002; 361: 57-265.
29. Derby N, Olbert S. Cylindrical magnets and ideal solenoids. Am J Phys. 2010; 78: 229-235.
30. Bulirsch R. Numerical calculation of elliptic integrals and elliptic functions. Numer Math. 1965; 7: 78–90.
31. Caciagli RJ, Baars AP, Philipse BWM, Kuipers. J MagnMagn Mater. 2018; 456: 423–432.