Indexed In
- Open J Gate
- Genamics JournalSeek
- JournalTOCs
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Publons
- Geneva Foundation for Medical Education and Research
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Review - (2023) Volume 14, Issue 2
Mechanisms of the Solid Cancer Induced by Atomic Bomb and the Spontaneous Cancer in the Daily Life-Proposal of a New Medical Treatment for Cancers-Review
Hiroshi Baba1 and Akihiko Yokoyama2*2Department of Medicine, Institute of Science and Engineering, Kanazawa University, Kakuma, Kanazawa, Ishikawa, Japan
Received: 02-Mar-2023, Manuscript No. JCRB-23-20035; Editor assigned: 06-Mar-2023, Pre QC No. JCRB-23-20035 (PQ); Reviewed: 20-Mar-2023, QC No. JCRB-23-20035; Revised: 27-Mar-2023, Manuscript No. JCRB-23-20035(R); Published: 05-Apr-2023, DOI: 10.35248/2155-9627.23.14.455
Abstract
Incidence rates of radiation-induced cancers and spontaneous cancers observed in the daily-life were analyzed to construct mathematical models respectively. Resulting models reproduced observed incidence rates satisfactorily. The former model is a two-stage process, damaging of a chemical bond in a cell by radiation and succeeding mutation of the damaged cell to a cancer. The latter is a one-stage process evoked by cell division.
For radiation-induced cancers, the curing effect was clearly observed for mild environmental radiation. Regrettably, no data are available for the effect of mild-level radiation on the spontaneous cancer observed daily-life, however the possibility that the damaged cell is affected by mild radiation is high since the damage caused by cell division should be much more severe compared to the collision with radiation.
Keywords
Atomic bomb; Mathematical models; Radiation-induced cancer; Spontaneous cancer
Introduction
The typical injury caused by atomic bombing in Hiroshima and Nagasaki districts is the cancer which was energetically followed by a group mainly consisting of the members of Radiation Effects Research Foundation (RERF) from 1975 to 1999 [1]. This valuable report is the only one quantitative document on the incidence rates for solid cancers among Hiroshima-Nagasaki A-bomb survivors.
In 1957, Armitage and Doll published a multistage model (AD model) for carcinogenesis of radiation-induced cancers [2]. It consists of damaged intermediate cells formed by irradiation of healthy cells and malignant cells produced by transformation of the unstable intermediate cells repeated for several times until the malignant cell reaches.
Several investigations were carried out using the RERF data. However, their interests were concentrated on the comparison of radiation risks among cohorts with respect to respect to sex, age at the time of bonding the mechanism of carcinogenesis [3-11]. Though the AD model is quite a reasonable model to explain radiation-induced cancer, it brought in some ambiguities into the model. The long lag required after formation of intermediate cells is settled as the time for statistical mutation of a damaged cell to the cancer cell. Thus, the multistage AD model was replaced by the simplest two-stage model.
We noticed the analogy between creation of intermediate cells by radiation of A-bombing and the production of radioactive nuclides by an accelerator and between mutation of generated intermediate cells and disintegration of radioactive nuclides.
Solid cancers caused by radiation are clinically indistinguishable from spontaneous cancers naturally occurring in the daily life. The incidences given by Preston et.al contain those of the spontaneous cancers [1]. We built a mathematical model for reported incidence rates containing the spontaneous cancer and devised an algorism deducing the magnitude of the spontaneous cancer by means of the time dependence of observed incidence rate.
Finally, we intended to clarify the mechanism of the spontaneous cancer observed in the daily life. We attended to the very remarkable age-dependence of incidence rates and concluded that the mutation takes place at the moment of cell division. With thus constructed whole story of cancers, we found the possibility of a harmless medical treatment of cancers using low-level radiation.
Mechanism of Solid Cancers Induced by Radiation
Solid cancers induced by radiation require quite long latent periods. In order to reproduce such latent periods, the phenomenon needs to be divided into two steps, the process giving damage to cells by radiation exposure and the transformation process of damaged cells to cancer cells.
TMechanism of the two-stage radiation-induced cancer consists of two fundamental radiochemical processes, mechanical collision between an impinging neutron, electron or photon and an electrons bound in a chemical bond to produce unstable cells, and a statistical event equivalent to the decay of radioactive nuclides [4-11].
This principle was applied to the investigated incidence data of solid cancers among Hiroshima-Nagasaki survivors to construct a mathematical model [1]. The first step producing radiation damage is a simple collision of impinging particles and bound electrons in the cell. The second step for the latent period is a statistical process following the first-order reaction, and can be treated as the radioactive decay, that is, the growth rate equation for the daughter nuclide in the radioactive decay.
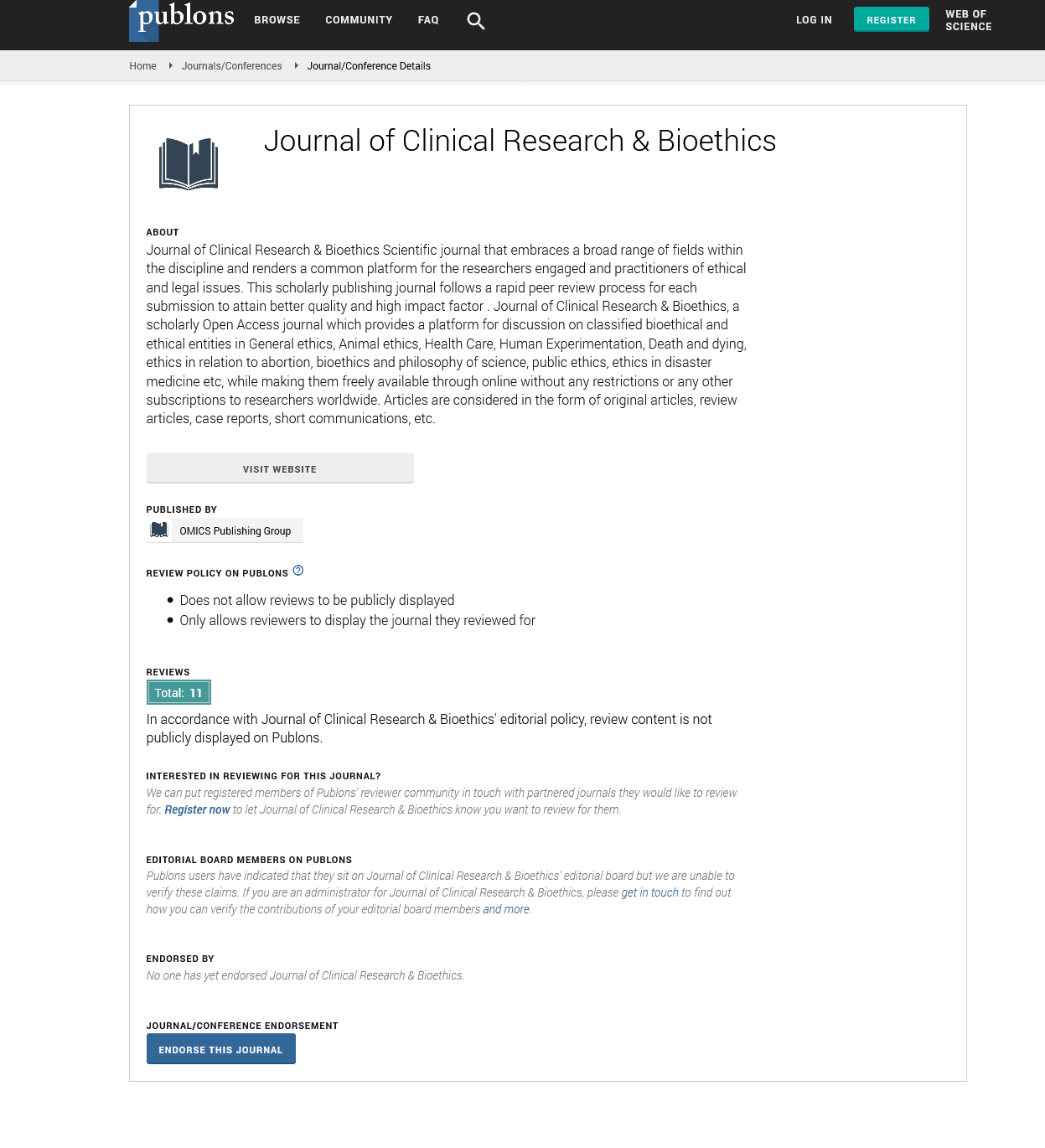
The number of normal cells remaining just after bombing is given by (1- γD)N0 with original number of normal cell N0 and the radiation dose at bombing D, where γ is the probability of producing damage. The number of damaged cells is given by γDN0. Then the change of damaged cells is shown in Equation (1).
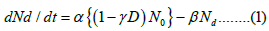
Here, the reaction rate constants and α, β are being used and D represents the proportion of damaged cells that were produced at the time of the explosion to the total cells. The number of normal cells at time t after bombing is the first term on the right side of Equation (2). The second term reflects the radiation-damaged condition's relaxing process, and it provides the relaxation process's rate constant. The solution of Equation (2) is given by,
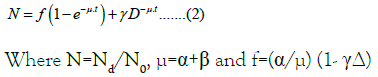
The continuous time variable is now replaced with an integer n corresponding to one year. That is, one year is regarded to be the unit of time. The factor for the latent period is introduced into the Equation (3)
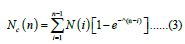
where Nc(n) is the number of cancer cells at the nth year after bombing and Λ is the rate constant of mutation. The incidence rate is given as the number of patients per 10 populations, so that we must replace the concept of the number of damaged cell by the number of patients [5]. This procedure may be allowed because the number of persons received multiple damages is expected to be negligibly small considering a quite low geometrical cross section for contact of radiation.
We can set a condition Λ < μ from the characteristics requested to Λ and Equation (4) is transformed as follows;
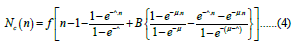
Here, B is a secondary parameter like μ and f defined by Equation (5).
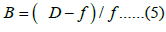
As is obviously seen, the incidence rate Nc is expressed with four parameters f, μ, Λ and B. However, f is a scaling factor and not an independent parameter excluded in the fitting procedure. The remaining three parameters should take the same value irrespective of the kind of cancer since the first stage should be a purely mechanical process.
The incidence rates given in the RERF report are the sum of people affected cancers for 5 years [1]. Therefore, Equation (6) is written as
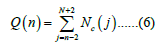
To compare the model with observed data.
Recently, Sato et al. of National Institute of Health, USA reported that they succeeded in reducing tumor of cancers of lung and large intestine by depleting regulatory T cells to activate the action of immune cells with generated heat by irradiation of near-infrared rays [12]. This would support an idea of coexistence of immune and anti-immune cells, and anti-immune cells are rather weak against outer actions including radiation.
Destruction of anti-immune cells by radiation is the first-order reaction and controlled by the same equation for the decay of radioactive nuclides. Then, the incidence risk of stomach cancer at n years after bombing is given by Equation (7).
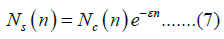
Then, the incidences for five years is given by Equation (8).
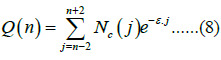
Let us transform Equation (8) by introducing a minor approximation of changing the exponential factor e-ɛ.j and e-ɛ.n to and taking the exponential factor out of the summation with respect to j. We further introduce a free parameter Qsc as the spontaneous incidence rate and a physical quantity ξ(n) shown in Equation (9).
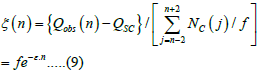
These procedure leads to an Equation (10).
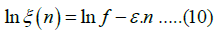
The spontaneous incidence rate Qsc is given by the point where the oblique line crosses the ordinate. The results of are shown for the half of the reported 33 cancers in Figure 1.
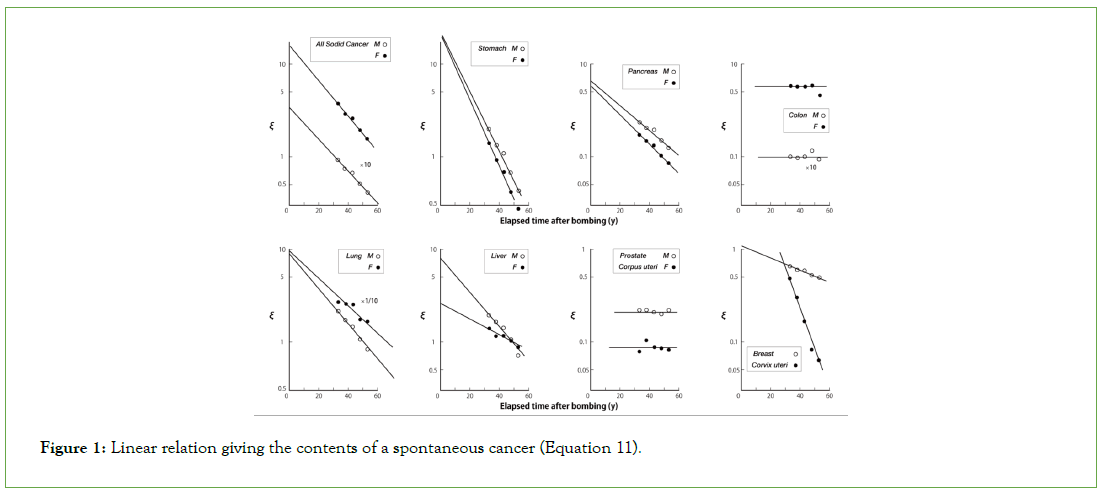
Figure 1: Linear relation giving the contents of a spontaneous cancer (Equation 11).
Net incidence rates subtracted Qsc were well reproduced with calculated values for all 33 cancers using a unique combination of three parameters μ, ^, B as indicated in Table 1. This result is a strong support for the proposition that the first stage of radiationinduced cancer is a purely mechanical phenomenon.
| Solid cancer | µ,^ ,β | B | ɛ | F=(x-5) | Α(x10-5) | Latent period(y) | ||
|---|---|---|---|---|---|---|---|---|
| Oral Cavity | M | (µ=0.05 ^=0.01 Β=µ) |
0.1 | 0.019 | 0.23 | 0.25 | 0.011 | 14 |
| F | 0.042 | 0.22 | 0.24 | 0.011 | ||||
| Esophagus | M | 0.019 | 0.33 | 0.36 | 0.016 | |||
| F | 0.085 | 0.72 | 0.79 | 0.036 | ||||
| Stomach | M | 0.073 | 22.2 | 24.4 | 0.011 | |||
| F | 0.082 | 21 | 23 | 0.05 | ||||
| Lung | F | 0.035 | 0.97 | 1.1 | 0.049 | |||
| Pancreas | M | 0.032 | 0.66 | 0.72 | 0.033 | |||
| F | 0.036 | 0.58 | 0.64 | 0.029 | ||||
| Kidney | M | 0 | 0.1 | 0.11 | 0.005 | |||
| F | 0 | 0.045 | 0.051 | 0.002 | ||||
| Breast | F | 0.015 | 1.1 | 1.2 | 0.055 | |||
| Cervix uteri | F | 0.1 | 12.4 | 13.6 | 0.62 | |||
| Bladder | M | 0.021 | 0.35 | 0.39 | 0.018 | |||
| F | 0.035 | 0.16 | 0.18 | 0.008 | ||||
| Thyroid | M | 0 | 0.021 | 0.023 | 0.001 | |||
| Brain | M | 0.02 | 0.45 | 0.5 | 0.023 | |||
| F | 0.03 | 0.13 | 0.14 | 0.007 | ||||
| Liver | F | 0.02 | 0.26 | 0.29 | 0.013 | |||
| Corpus uteri | F | 0 | 0.087 | 0.096 | 0.004 | |||
| Rectum | M | -0.3 | 0 | 0.1 | 0.07 | 0.005 | 17 | |
| Prostate | M | -0.3 | 0 | 0.1 | 0.07 | 0.005 | 17 | |
| Rectum | F | -0.5 | 0 | 0.35 | 0.18 | 0.018 | 19 | |
| Ovary | F | 0 | 16.1 | 0.06 | 0.006 | |||
| All solid Cancers | M | -0.7 | 0.041 | 33.5 | 10.1 | 1.68 | 22 | |
| F | 0.045 | 16.1 | 4.8 | 0.81 | ||||
| Lung | M | -0.9 | 0.045 | 90 | 0.9 | 0.45 | 25 | |
| Liver | M | 0.043 | 8.1 | 0.8 | 0.41 | |||
| Colon | M | 0 | 1.02 | 0.06 | 0.051 | |||
| F | 0 | 0.58 | 0.7 | 0.029 | ||||
| Gallbladder | M | 0.066 | 7.3 | 0.7 | 0.37 | |||
| F | 0.085 | 11.2 | 1.1 | 0.65 | ||||
| Thyroid | F | 0.035 | 1.3 | 0.13 | 0.065 | |||
Table 1: Parameters extracted for net radiation-induced incidences.
Mechanism of Spontaneous Cancers in the Daily Life
Now that the formulation of radiation-induced solid cancers is cleared, our next target is formulation of the daily-life spontaneous cancers. It is more serious problem to formulate the mechanism of spontaneous cancers, contrary to the former induced only in the emergency. However, any systematic yearly change in the incidence is not expected to appear among patients of spontaneous cancer contrary to the radiation-induced cancers. So, we must look for other sources of data on which we construct a mathematical model.
The risk of a cancer starts at the moment of birth and people keep staying under the risk thereafter. The age therefore corresponds to the exposed duration of Hiroshima-Nagasaki survivors. The data of yearly cancer incidence rates of age groups for 5 years given by National cancer center, Japan are our subjects to try to construct the mathematical model of the spontaneous cancer (Figure 2) [13- 16].
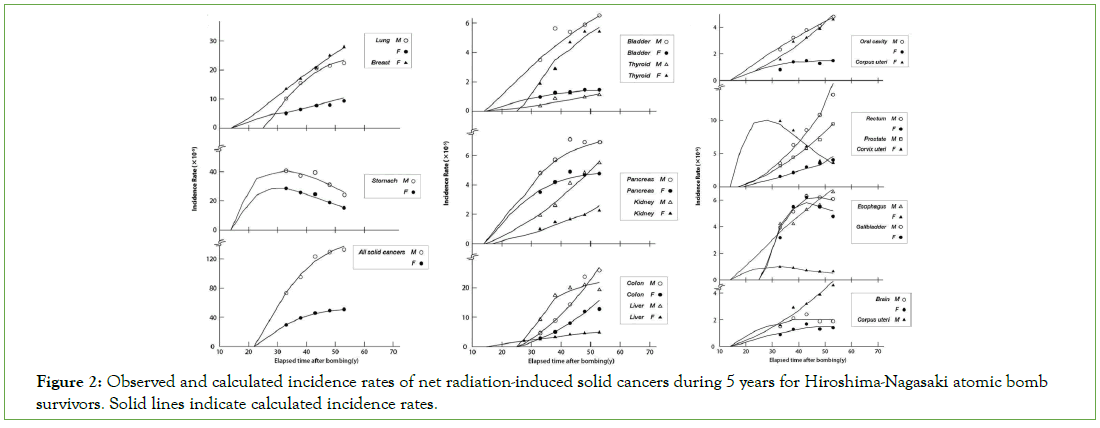
Figure 2: Observed and calculated incidence rates of net radiation-induced solid cancers during 5 years for Hiroshima-Nagasaki atomic bomb survivors. Solid lines indicate calculated incidence rates.
The devised model is based on the abnormal cell division. The incidence rate stays at very low level below middle age and begins to increase quite violently thereafter [16]. This lets us think of increase of the number of cells in the cell division and increase of abnormal cells produced at division.
However, the increasing rate of the number of cells is turned out too large to reproduce the incidence rate when we compute the number of cells with the condition that two cells are produced at each division. In order to avoid the catastrophe, we introduced programmed death of cell (apoptosis) to our model, as in Equation (11)
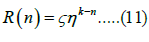
Where ζ is the probability of occurrence of abnormal division at cell division, ɳ is the number of surviving cells at cell division, and k is the number of times of division occurring during a year [17].
This simple equation reproduces well the available incidence rates of 33 solid cancers and 4 data of Leukemia and Lymphoma given for the age groups from twenties to fifties [16]. However, calculated values still substantially exceed observed values for age groups above the fifties. The possible way of avoiding this discrepancy may be attributed to the aging effect, which was introduced into Equation (11).
The discrepancy in Equation (11) should be attributed to either k or ɳ. As a result of examination, we reached a conclusion that only reduction of ɳ for high generation can cover the discrepancy.
It is then assumed that ɳ stays constant until it starts to linearly decrease at the age n0 in the aging effect, namely shown in Equation (12).
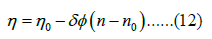
For n ≤ n1, where ɸ is a function shown in Equation (13) and shown in Equation (14).
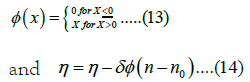
for n>n1.
The recursion work with age-dependent incidence rates averaged over five years from 1995 to 1999 was repeated until getting a self-consistent solution for the introduced parameters for an appropriately given k value [16]. The best result was obtained for k=0.9 (13 months as the time between the adjacent divisions), and the value of n0 and the resulting functional form of for each cancer is given as a combination of a constant part and linearly decreasing section above a critical age n0.
The resulting incidence rates are shown in Figure 3 in comparison
with the observed values. All cancers were found controlled with
two principal parameters, k and n0. The k was kept constant
throughout all cancers. They were classified into four groups
assigned with specific values of n0. Difference in the situation, such
as site of cancer, sex, habits, medical treatment, etc. appears only in
ζ and aging effects ɳ, and have no influence on the fundamental structure of the mechanism of spontaneous cancers. It is notable
that all cancers including breast, ovary and uterus revealing irregular
feature can be explained by a single equation. 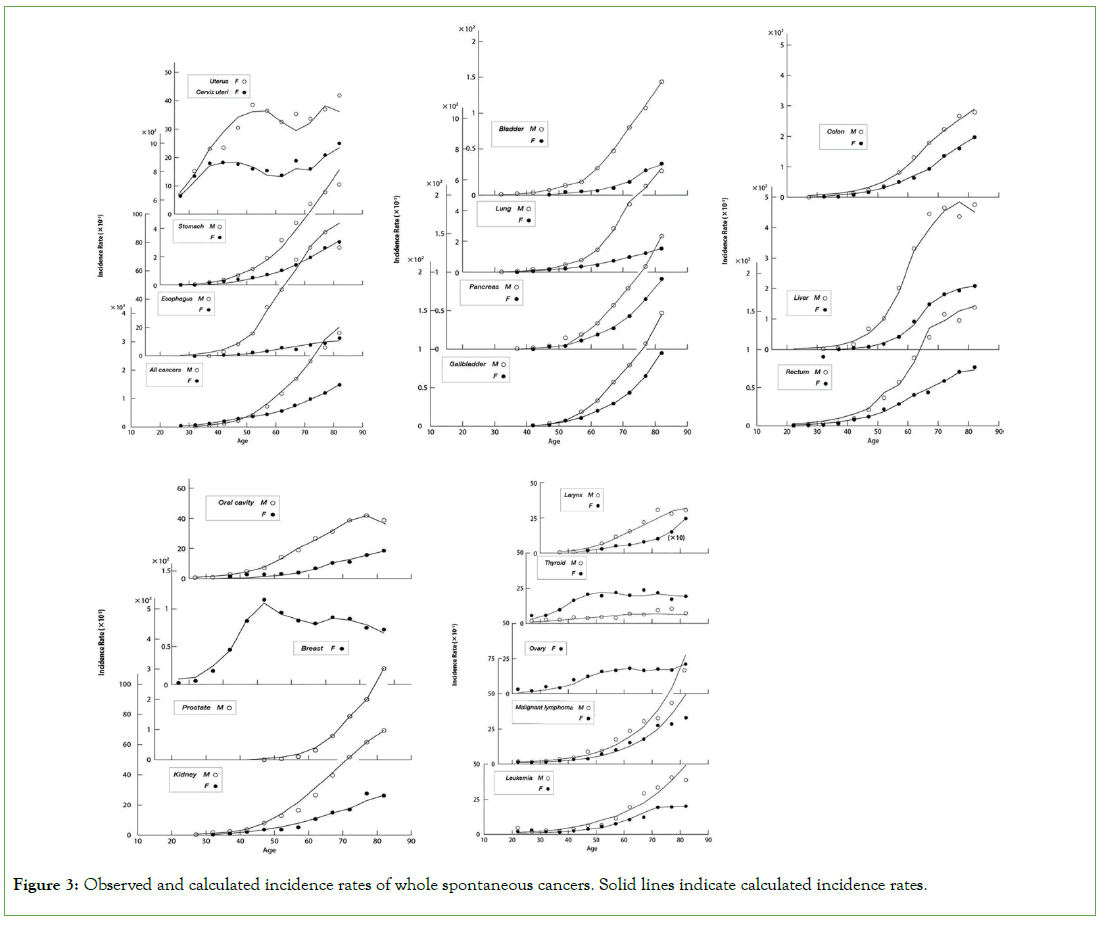
Figure 3: Observed and calculated incidence rates of whole spontaneous cancers. Solid lines indicate calculated incidence rates.
Discussion
The present model for radiation-induced cancers satisfactorily reproduces the incidence rates of all reported cancers without any exception and therefore would have strong persuasiveness. According to this model, observed strong immune effects are explained by means of destruction of immune-restraint cells by rather low−level environmental radiation during several ten years after the bombing, not by radiation of high dose at the moment of bombing. This implies that immune-restraint cells possess only very low tolerance against radiation.
The most noteworthy item is the result that μ, Λ and B take common values, respectively, throughout the cancers. This indicates the processes controlled by the above three parameters are the purely mechanical process nevertheless their pathological differences. On the other hand, the probability f of producing radiation damage and the parameter ɛ giving the immune effect respectively take a different value for individual cancer and concluded to be controlled by biological or pathological factors.
Reported incidence rates of most cancers show exponential decrease from the time of bombing. This implies that the damaged cells are destroyed by environmental radiation. No available data exists concerning the effect of mild radiation on cell division. However, damages which cells receives at cell division should be much severer than the one produced by radiation and so the possibility that radiation works to kill damaged cell at cell division is expected to be quite high. If this is proved, we can give a great hope to the patients at late stage being able to receive existing medical treatment.
The model constructed for spontaneous cancers explains well the observed incidence rates. Furthermore, the physical scenario does not contradict the two-stage clonal expansion or multi-stage carcinogenesis model for cancers [2,18].
Conclusion
Formulation of spontaneous cancers leads to the conclusion that the cancer is induced with the cells lost the function of apoptosis at abnormal cell division. In general, apoptosis is explained as a phenomenon occurring on the useless or incomplete cells. Apoptosis called in the present model requires the function that cells generated at the cell division are always extinguished with the definite and unexpectedly large ratio. When this treatment is proved effective, patients once suffered by cancer will be relieved from the fear of recurrence of cancer without any severe side effect.
References
- Preston DL, Ron E, Tokuoka S, Funamoto S, Nishi N, Soda M, et al. Solid cancer incidence in atomic bomb survivors: 1958-1998. Radiat Res. 2007;168(1):1-64.
[Crossref] [Google Scholar] [Pubmed]
- Armitage P, Doll R. The age distribution of cancer and a multi-stage theory of carcinogenesis. Br J Cancer. 2004;91(12):1983-1989.
[Crossref] [Google Scholar] [Pubmed]
- Rühm W, Eidemüller M, Kaiser JC. Biologically-based mechanistic models of radiation-related carcinogenesis applied to epidemiological data. Int J Radiat Biol. 2017;93(10):1093-117.
[Crossref] [Google Scholar] [Pubmed]
- Little MP. Generalisations of the two-mutation and classical multi-stage models of carcinogenesis fitted to the Japanese atomic bomb survivor data. J Radiol Prot. 1996;16(1):7.
- Little MP. Cancer models, genomic instability and somatic cellular Darwinian evolution. Biology direct. 2010;5:1-9.
[Crossref] [Google Scholar] [Pubmed]
- Little MP. Are two mutations sufficient to cause cancer? Some generalizations of the two-mutation model of carcinogenesis of Moolgavkar, Venzon, and Knudson, and of the multistage model of Armitage and Doll. Biometrics. 1995:1278-1291. [Crossref]
[Google Scholar] [Pubmed]
- Little MP, Muirhead CR, Stiller CA. Modelling lymphocytic leukaemia incidence in England and Wales using generalizations of the two‐mutation model of carcinogenesis of Moolgavkar, Venzon and Knudson. Stat Med. 1996;15(10):1003-1022.
[Crossref] [Google Scholar] [Pubmed]
- Kai M, Luebeck EG, Moolgavkar SH. Analysis of the incidence of solid cancer among atomic bomb survivors using a two-stage model of carcinogenesis. Radiat Res. 1997;148(4):348-358.
[Crossref] [Google Scholar] [Pubmed]
- Heidenreich WF, Luebeck EG, Moolgavkar SH. Some properties of the hazard function of the two‐mutation clonal expansion model. Risk Anal. 1997;17(3):391-399.
[Crossref] [Google Scholar] [Pubmed]
- Izumi S, Ohtaki M. Aspects of the Armitage–Doll gamma frailty model for cancer incidence data. Environmetrics. 2004;15(3):209-218.
- Van Dillen T, Dekkers F, Bijwaard H, Kreuzer M, Grosche B. Lung cancer from radon: a two-stage model analysis of the WISMUT Cohort, 1955-1998. Radiat Res. 2011;175(1):119-130.
[Crossref] [Google Scholar] [Pubmed]
- Warren JR, Marshall BJ. Unidentified curved bacilli on gastric epithelium in active chronic gastritis. Lancet. 1983;1(8336):1273.
[Pubmed]
- Tatematsu M, Yamamoto M, Shimizu N, Yoshikawa A, Fukami H, Kaminishi M, et al. Induction of glandular stomach cancers in Helicobacter pylori‐sensitive Mongolian gerbils treated with N‐methyl‐N‐nitrosourea and N‐methyl‐N′‐nitro‐N‐nitrosoguanidine in drinking water. Jpn J Cancer Res. 1998;89(2):97-104.
[Crossref] [Google Scholar] [Pubmed]
- Uemura N, Okamoto S, Yamamoto S, Matsumura N, Yamaguchi S, Yamakido M, et al. Helicobacter pylori infection and the development of gastric cancer. N Engl J Med. 2001;345(11):784-789.
[Crossref] [Google Scholar] [Pubmed]
- Sato K, Sato N, Xu B, Nakamura Y, Nagaya T, Choyke PL, et.al. Spatially selective depletion of tumor-associated regulatory T cells with near-infrared photoimmunotherapy. Sci Transl Med. 2016;8(352):352.
[Crossref] [Google Scholar] [Pubmed]
- National Cancer Center website
- Kerr JF, Wyllie AH, Currie AR. Apoptosis: a basic biological phenomenon with wideranging implications in tissue kinetics. Br J Cancer. 1972;26(4):239-257.
[Crossref] [Google Scholar] [Pubmed]
- Nordling C. A new theory on the cancer-inducing mechanism. Br J Cancer. 1953;7(1):68.
[Crossref] [Google Scholar] [Pubmed]
Citation: Baba H, Yokoyama A (2023) Mathematical Models of the Solid Cancer Induced by Atomic Bomb and the Spontaneous Cancer in the Daily Life-Proposal of a New Medical Treatment for Cancers. J Clin Res Bioeth. 14:455.
Copyright: © 2023 Baba H, et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.