Indexed In
- Genamics JournalSeek
- JournalTOCs
- CiteFactor
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Publons
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Research - (2019) Volume 8, Issue 2
Interface Liquid-Solid: Global Bifurcation Multiparameter of Flow Water Waves through Porous Compacted Granular by “Yakam Matrix”
Leonard Kabeya-Mukeba Y*Received: 11-Sep-2019 Published: 27-Nov-2019
Abstract
The construction of the tourbillon balls is fundamentally well known to Constatin and Strauss. In this work, we apply the flow of water through the compacted granular, in order to arrive at a model of passage in confinement and stagnation through the pores. An approach agrees of the advanced theory of water waves and the application of dynamics in microfluidics is discussed to improve “ASEAD Project water for everybody”. The approximation solution of nonlinear stochastic partial differential equation for only element of “Yakam Matrix” liquid-solid interface by simple understanding bifurcation behavior will follow the some trajectory of waves of water, granular compaction and dynamics of fluids at all scales, then we are still just at the beginning.
Keywords
Water; Flow; Bifurcation; Multivariable; Granular; Pores; Yakam Matrix
Introduction
In many cases, we find differential equations and partial differential equations, which justify the different variations of physical, chemical, biological or other phenomena, using five well-known physical states of matter. These are: the solid state (s), the liquid state (l), the gaseous state (g), the plasma state and the colloidal state. These states allowed us to build a matrix called Yakam introduced for the first time in 2007 [1].
We consider the Stokes equation governing the velocity and
pressure of an incompressible creeping flow, subject to the gravity,
in a domain Ω, open bounded subset of Rd. As the flow is supposed
to be sufficiently slow to neglect the advection compared to the
diffusion, the momentum balance equation reduces to 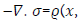

With the stress tensor 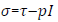 Consisting of a viscous stress
tensor and pressure term with I the identity matrix of Md (R).
The incompressible constraint (x,,)=0. Moreover, the relation
between liquid and granular through pores of Nano diameters
gave supplemented with boundary conditions dΩ. In practice
one cylinder with three dimensional in viscid gravity waves at the
surface of layer of water with a flat bottom is the build case.
Consisting of a viscous stress
tensor and pressure term with I the identity matrix of Md (R).
The incompressible constraint (x,,)=0. Moreover, the relation
between liquid and granular through pores of Nano diameters
gave supplemented with boundary conditions dΩ. In practice
one cylinder with three dimensional in viscid gravity waves at the
surface of layer of water with a flat bottom is the build case.
This interface helps the simple Setup, where undisturbed state of flat surface equation is y=0 and the flat bottom is given by y=-d for some d>0. In the presence of waves, let y=n(t, x) be the free surface and let (u(t, x, y, z)), v(t, x, y, z), w(t, x, y, z)) be the velocity field (Figure 1). If P (t, x, y, z) denotes the pressure, Po the constant atmospheric pressure, and g is the gravitational constant of acceleration, the governing equations [2,3] are:
Figure 1: Interface liquid-solid-drinking water.
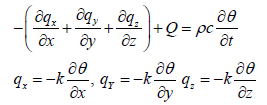
Where, k is the thermal conductivity of media. Substitution of Fourier’s relation gives the following basic flow equation:
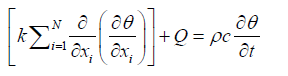
The specified pressure, volume and ambient temperature are 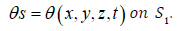 The specified flow
The specified flow 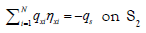 and the convection boundary conditions is
and the convection boundary conditions is 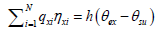 on S3.
on S3.
For coupled phenomena’s during interaction near the granular the
contact with solid gives 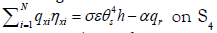 where σ is
Stephan-Boltzmann constant, ε is the surface emission coefficient;
α is the surface absorption coefficient and qr is coming flow per
unit surface area. For transient problems it is necessary to specify
a pressure field for a body at the time t=0; θ(x, y, z, 0)=θ0(x, y, z).
where σ is
Stephan-Boltzmann constant, ε is the surface emission coefficient;
α is the surface absorption coefficient and qr is coming flow per
unit surface area. For transient problems it is necessary to specify
a pressure field for a body at the time t=0; θ(x, y, z, 0)=θ0(x, y, z).
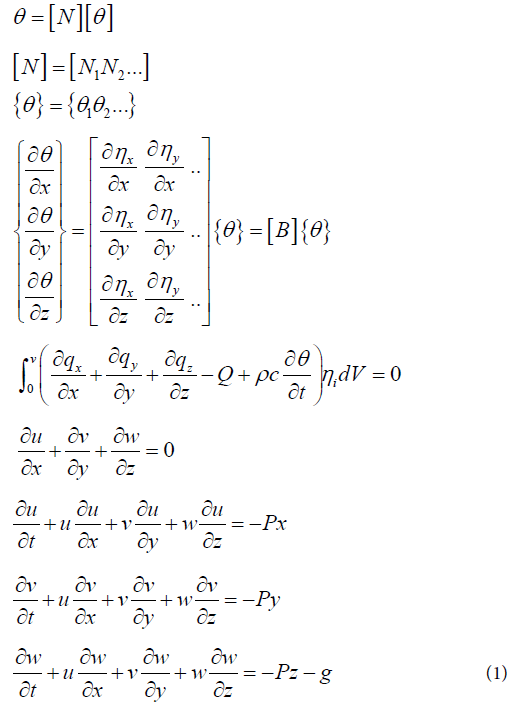
The boundary conditions for the water wave problem are P=P0 on y= 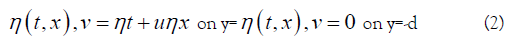
Given c>0, we are looking for periodic waves traveling at speed c. The
profile η oscillates around the flat surface y=0 and the horizontal
fluid velocity u is less than c at every point. For convenience we
shall take the length scale to be 2π . Define the (relative) stream function 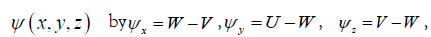 with
with 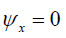 on the free surface, and let
on the free surface, and let  be the vorticity
be the vorticity  At least locally, away from a stagnation point (a point where u=c, v=d, w=0), ω is a function of Ψ . We will assume
that there is a functionγ , called the vorticity function, such that
ω =γ (ψ ) throughout the fluid. Thus, Δψ = −γ (ψ ). We define the
relative mass flux as
At least locally, away from a stagnation point (a point where u=c, v=d, w=0), ω is a function of Ψ . We will assume
that there is a functionγ , called the vorticity function, such that
ω =γ (ψ ) throughout the fluid. Thus, Δψ = −γ (ψ ). We define the
relative mass flux as 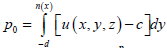 , which is independent of x by (2). Since
, which is independent of x by (2). Since 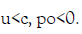 Let
Let 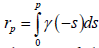 have minimum value
have minimum value 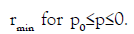 Let
Let 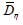 be the closure of the open fluid domain
be the closure of the open fluid domain 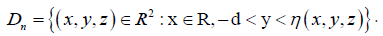 Given as set E
with a smooth boundary, define for ∈N and α ∈ (0,1) the space
Given as set E
with a smooth boundary, define for ∈N and α ∈ (0,1) the space 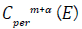 of functions
of functions 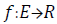 with Holder continuous derivatives
( of index α) up to order m and of period 2π in the x, y and z
variables. Our main results are as follows (Figure 2).
with Holder continuous derivatives
( of index α) up to order m and of period 2π in the x, y and z
variables. Our main results are as follows (Figure 2).
Figure 2: Main results with the x, y and z variables.
Theorem 1
Let the wave speed c>0, the relative mass flow po<0 and an arbitrary
α∈ (0,1) be given. Let y(s) be a C1+α function defined on [0,|po|]
Such that 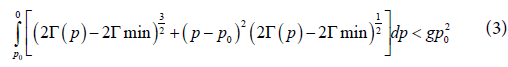 And
And 
Consider traveling solution of speed c of the water wave problem
(1)–(2) with vorticity function such that u<c throughout the fluid.
There exists a connected set C of solutions (u,,,) in the Space 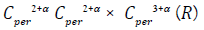 appropriated to Sobolev Space
for Nonlinear Partial Differential Equation, with the following
properties.
appropriated to Sobolev Space
for Nonlinear Partial Differential Equation, with the following
properties.
1. C contains a trivial flow (with a flat surface η=0 );
There is a sequence of solutions 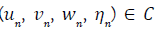 for which
for which 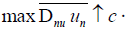
Furthermore, each solution 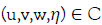 satisfies.
satisfies.
1. It is easily that 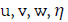 have period 2π in axis of gravitation
z;
have period 2π in axis of gravitation
z;
2. Within each period the wave profile η has a single maximum (crest) at x=a, say, and a single minimum (through);
3. That u and η are symmetric while v is antisymmetric around the line x=a;
4. 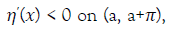 , i.e., the profile of the wave is strictly decreasing from crest to trough.
, i.e., the profile of the wave is strictly decreasing from crest to trough.
Therom 2
(i) We make the same assumptions as in theorem 1, except we do
not assume (4). Then there exists a connected set C with the same
properties as in Theorem 1, except that 5 ii) is replaced by (B*)
there is a sequence (Un) at either 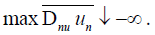
Discussion
History of Stokes
In 1847 Stokes [4] studied irrotational periodic traveling water waves
and some of their nonlinear approximations. The flat approach
was developed Levi-civita [5] and Struik [6]. Nevertheless in this
work we construct a global continuum of such regular solutions
with general vorticity. After that no other bifurcation point λ*
can have this nodal pattern and the pattern persists all along C
the nonlinear boundary condition. We reduce the alternative (a)
that C is unbounded in 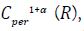 to the condition that
to the condition that 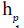 is
unbounded in
is
unbounded in 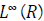 , then we prove that h is successively bounded
in
, then we prove that h is successively bounded
in 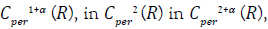 and finally in
and finally in 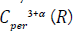 in
in  Here we use the Schauder estimates and several basic
a priori estimates of Lieberman and Trudinger [7] for nonlinear
elliptic equation with nonlinear oblique boundary conditions.
Here we use the Schauder estimates and several basic
a priori estimates of Lieberman and Trudinger [7] for nonlinear
elliptic equation with nonlinear oblique boundary conditions.
Application
Thus alternatives are reduced to (a*) either  is unbounded in L∞
(R), or (c) C contains in its closure a solution where
is unbounded in L∞
(R), or (c) C contains in its closure a solution where  vanishes.
Then we return to the original problem in the form of the Euler
equation. Under assumption (4) we eliminate the last possibility
(c) However, (a*) means that max
vanishes.
Then we return to the original problem in the form of the Euler
equation. Under assumption (4) we eliminate the last possibility
(c) However, (a*) means that max 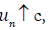 , while (c) means that min
, while (c) means that min
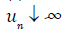 for some sequence of solutions.
for some sequence of solutions.
Compacted granular
Granular matter has been the subject of numerous studies since two last decades [G1-G2] for two–dimensional granular system [G2] and some the propagation of two-dimensional [G3] inviscid gravity waves at the surface of a layer of water with a flat botton.
Many manipulations of granular by compaction to properties powders are well-known, but the manipulation the adhesion liquid onto compacted granular in four different scales: macroscopic scale, mesoscopic scale, microscopic scale and nanoscale is very complex and present the nonlinearity of behaviour waves water onto substrates solid of compacted granular throughout the porous. Interface liquid-solid generate by nonlinear dynamical system. The models developed can help to understand and make predictions about effects induced by multipara meters change such onto during flow liquid, stagnation and flow in porous of granular and amplitude of periodic stimulus. The multi-disciplinary team of scientists and support staff whose aim is to investigate the occurrence of scrapie in the water of world population and to provide advice on the control of penery of drinking water in the future. We do not understand if the complex of element‘s “Yakam Matrix” can in physical sciences; scientific understanding has been expressed in elegant theoretical constructs and has led to revolutionary technological innovation [8-11]. If the advances in understanding bifurcation behavior of liquid-solid interface of “Yakam Matrix” will follow the some trajectory of waves of water, granular compaction and dynamics of fluids at all scales, then we are still just at the beginning “Yakam Matrix”.
The study of networks pervades all of science, from fluids mechanics. The nonlinear dynamics: systems can often be modelled by differential equations dx/dt=v(x), where x(t)=(x1(t), …, Xn(t)) is a vector of state variables, t is time, and v(x)=(V1(x),…, Vn(x)) is a vector of functions that encode the dynamics.
Terminology and Concepts
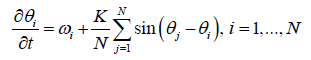
Where 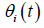 is the phase of the ith oscillator and i
ω is its natural
frequency, chosen at random from a lorentzian probability density
is the phase of the ith oscillator and i
ω is its natural
frequency, chosen at random from a lorentzian probability density 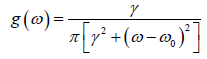 of width γ and mean
of width γ and mean 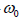 . Using an
ingenious self-consistency argument, Kuramoto solved for the
order parameter that
. Using an
ingenious self-consistency argument, Kuramoto solved for the
order parameter that 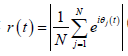 (a convenient measure of the
extent of synchronization) in the limit
(a convenient measure of the
extent of synchronization) in the limit 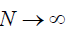 and
and 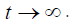 He
found that
He
found that 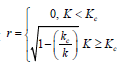
Where 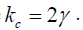 In order words, the oscillation and stagnation of
water through porous of granular are desynchronized completely
until the coupling strength K exceeds a critical value kc . After
that, the population splits into a partially synchronized three
dimensional state.
In order words, the oscillation and stagnation of
water through porous of granular are desynchronized completely
until the coupling strength K exceeds a critical value kc . After
that, the population splits into a partially synchronized three
dimensional state.
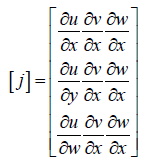
Conclusion
The partials derivatives of x, y, z, in respect to u, v, w are found by differentiation of displacement of water through porous of granulars.
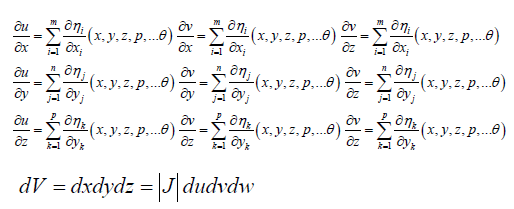
We limit our investigation in Hilbert-Sobolev Spaces specified by 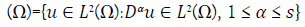
For our study  “noyau” of operator of
“noyau” of operator of  in
in 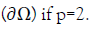
REFERENCES
- Mukeba LK. Pinning study of contact line during droplet evaporation, PhD Dissertation, University of Liege, Belgium, 2007.
- Johnson RS. A modern introduction to the mathematical theory of water waves, Cambridge University Press, UK, 1997.
- Contanton A. Walter Strauss, Exact periodic traveling water waves with vorticity, CRAcad Sci Paris, Ser. 2002;1335:797-800.
- Stokes G. On the theory of oscillatory waves, Trans. Cambridge Philos Soc. 1847;8:441-455.
- Levi-Civita T. Determinazione rigorosa delle onde irrotazionali periodiche in acqua profonda. Rend Accad Lincei. 1924;33:141-150.
- Struik D. Détermination rigoureuse des ondes irrotationnelles périodiques dans uncanal àprofondeur finie. Math Ann. 1926;95:595-634.
- Lieberman G, Trudinger N. Nonlinear oblique boundary value problems for nonlinear elliptic equations. Trans Amer Math Soc 1986;295:509546.
- De Gennes PG. Granular matter: A tentative view. Rev Mod. Phys. 1999;71:S374.
- Lumay G, Vandewalle N. Experimental study of granular compaction dynamics and different scales: grain mobility, hexagonal domains, and packing fraction. Physical Review Letters. PRL. 2005;95:028002.
- Constantyin A. Walter Strauss, Exact periodic traveling water waves with vorticity, CRAS Paris, Ser I. 2002;335:797-800.
- Boyer F, Fabrie P. Mathematical tools for the study of the incompressible Navier–Stokes equations and related models. Springer Series: Applied Mathematical Sciences. Springer, 2013.
Citation: Kabeya-Mukeba LY (2019) Interface Liquid-Solid: Global Bifurcation Multi-parameter of Flow Water Waves through Porous Compacted Granular by “Yakam Matrix”. J Appl Mech Eng. 8:321. doi: 10.35248/2168-9873.19.8.321
Copyright: © 2019 Kabeya-Mukeba LY. This is an open access article distributed under the term of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.