Indexed In
- Open J Gate
- Academic Keys
- RefSeek
- Hamdard University
- EBSCO A-Z
- Publons
- Geneva Foundation for Medical Education and Research
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Research Article - (2020) Volume 8, Issue 4
Healthcare without Health Insurance: A Peer to Peer Healthcare Payment Platform
Bose A*Received: 09-Aug-2020 Published: 18-Sep-2020, DOI: 10.35248/2375-4273.20.8.257
Abstract
In this paper, I present a method for a peer to peer payment network which will allow members to share the cost of their medical bills. The proposed P2P payment system could replace the traditional health insurance model and save more than $ 83B annually in USA which is the administrative cost of top six health insurance companies. First, an economic analysis of the current health insurance model is presented to allow the readers who are not familiar with US health care system to understand the current challenges. Following this, I present the "pairing members" theorem which attempts to establish the foundation of the economic validation of the proposed methodology. Finally, I present the frame work on which the algorithm of payment is developed. A Monte Carlo simulation technique is used to generate Medical Benefit Expenses of a small set of children, and then the method for identifying pairing members is applied. I also discuss the future direction of research and implementation plan of the proposed network.
Keywords
Health; Insurance; Economic
Introduction
Since 1980 total healthcare expenditure in USA as a percentage of GDP is rising faster than that in OECD countries [1]. The total expenditure is a function of cost per unit service multiplied by per capita consumption of service. In USA, cost per unit service is rising due to technological innovation and consumption of service is increasing as prescribers are prescribing more tests to avoid law suits; and patients are using more services than needed as they believe cost is paid by commercial insurance and/or Medicare which is funded by Federal government [2]. The paper on medical waste addresses these issues in depth [3]. The result of this behavior is that healthcare cost is rising at an alarming rate.
In order to compensate for the rising healthcare cost, commercial insurance providers are raising the insurance premium. A complete review on insurance rates during 2002-09 is presented in [4]. A more recent report on insurance rates during 2009-18 is available in [4,5]. As documented in the premiums charged by health insurance companies represent actuarial estimates of the amount that would be required to cover three main components: (i) the expected cost of the health benefits covered under the plan, (ii) the business administrative costs of operating the plan, and (iii) a profit. The Affordable Care Act (ACA) imposed an upper limit on the administrative cost as a percentage of the total premium collected from members. As the medical cost is rising since 2009, the administrative cost rose in parallel. In 2019, the total premium collected by top six health insurance companies in USA is $465.6B as documented in [6,7]. The management and administrative cost is $83.8B per year for these six insurance companies. The objective of the present work is to analyze a peer to peer healthcare payment network by which the traditional health insurance model could be eliminated completely.
The rest of the paper is organized as follows. In Section 2, current approach on the administrative cost reduction is discussed; then the mathematical description of the problem is presented. In Section 3, an algorithm for identification of thepairing member’s problem is described. In Section 4, I present a framework for P2P Network for Payment system. Section 5 shows Monte Carlo simulation results, comparisons and discussion. A conclusion and directions for future work are done in Section 6.
Background
There have been many debates on the issue of national health insurance in USA. A brief description and comparison of the three national health insurance proposals is presented in [8]. Employer mandated health insurance and Refundable Tax Credit (with or without an Individual Mandate) have high administrative costs due to multiple health plans, monitoring and enforcement of mandate. The Single-Payer System has low administrative cost. It is too low detected fraud and abuse or to institute disease management and other types of cost containment programs.
A. Comparison between Traditional Insurance and A Peer to Peer Payment System
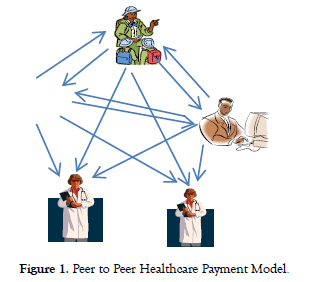
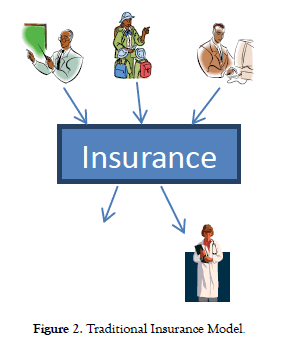
As shown in Figure 1, the structure of proposed Peer to Peer (P2P) payment model is fundamentally different than the traditional insurance model shown in Figure 2.
Figure 1. Peer to Peer Healthcare Payment Model.
Figure 2. Traditional Insurance Model.
The basic principle of insurance is transfer of risk. The insured member transfers the risk to an insurer (an insurance company); in exchange, the insurer earns money in premium. As the cost of healthcare is rising, the risk of a member is going up. This is causing the rise of medical insurance premium. Instead of transferring the risk to an insurance company, members can exchange risk among each other. This is possible because some members have relatively lower risk than others. By using the principle of exchange of risk among members, we can design a payment system which will allow us to eliminate the massive insurance companies structure which takes away more than $ 83B annually from the providers and patients.
B. Definition of Peer to Peer Network
In this paper, I shall follow the definition of Peer to Peer network as presented in [9].
A distributed network architecture may be called a Peer-to-Peer (P-to-P, P2P.) network, if the participants share a part of their own hardware resources (processing power, storage capacity, network link capacity, printers, ...). These shared resources are necessary to provide the Service and content offered by the network (e.g. file sharing or shared workspaces for collaboration): They are accessible by other peers directly, without passing intermediary entities. The participants of such a network are thus resource (Service and content) providers as well as resource (Service and content) requestors (Servant-concept).
Following the above definition, we can see the justification for using the P2P model to eliminate the need for a traditional insurance company. Each patient in the network can have the dual role of payer and borrower.
There are several applications of P2P network architecture in healthcare. Examples of P2P network in healthcare are presented in [10,11]. However, to the best of my knowledge, there is no published work on the application of P2P network payment system to replace administrative functions of traditional health insurance.
C. An Economic Analysis of P2P Payment Model
Before I present the economic analysis, I would like to discuss some definitions of Terms used in the proposed P2P Payment model:
i. Network of Patients: A group of persons who use medical services offered by doctors, hospitals and clinics. They have different levels of risks due to different medical conditions, age etc.
ii. Network of Payers: A group of organizations (employers, NGOs, government and foundations) and/or individuals who pay to the network of patients. The payment could be onetime payment (ex. Copay assistance) to a specific patient, or it could be a monthly payment to a patient (ex. Benefit to an employee)
iii. Network of Service Providers: A group of doctors, nurses, hospitals and clinics who provide medical services to the network of patients for a certain amount of fee. This network is not similar to the network of providers used by a traditional insurance company.
List of Symbols used in Economic Analysis:
A,B=Members of an insurance company
MBE=Medical Benefit Expense
P(A), P(B)=Profit generated from A , B
P(MAX)=Maximum profit generated from a member of an insurance company
F1(A),F1(B)=Contribution by employer for A, B
F2(A),F2(B)=Insurance Payment by A, B
F3(A),F3(B)=MBE for A, B
O(A),O(B)=Operational cost for A, B
M(A),M(B)=Marketing cost for A, B
EWR=Employer Worker Ratio=F1/F2
Subscript Definitions
F3e= Estimated MBE
MBETarget=Target MBE set by insurance
MBEPairing-member=A variable used to identify the pairing member, given a target MBE and one of the members
Delta (xi) = Distance of xi from MBETarget
Xi = i-th element in the list of members
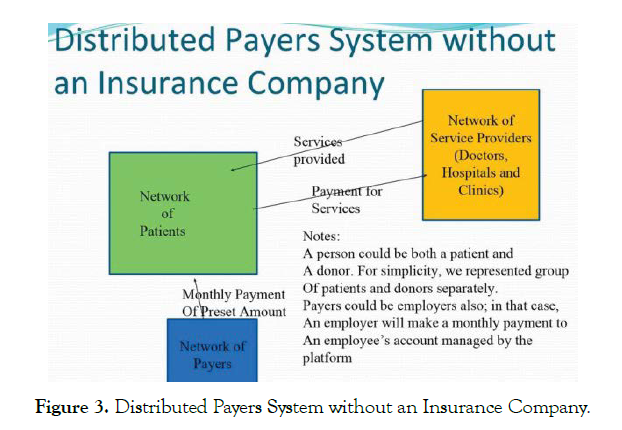
The relationship between network of patients, network of payers and network of service providers is shown in Figure 3. Please note that payers do not pay to the providers directly which contrasts with the traditional insurance model. The network of patients is responsible for paying medical bills from the network of service providers. The obvious question is: how will a patient pay very large medical bill? I will address this question in section IV.
Figure 3: Distributed Payers System without an Insurance Company.
A person could be both a patient and a payer. For simplicity, we represented group of patients and donor’s separately. Payers could be employers also; in that case, an employer will make a monthly payment to an employee’s account managed by the platform.
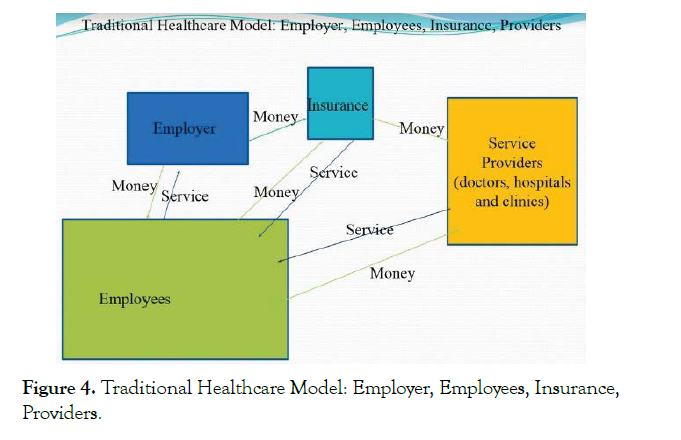
At this point, I would like to present the notion of “pairing members” which is an important aspect of the proposed model. To illustrate the “pairing members”, I shall first analyse the relationship among various actors in the traditional health insurance model as shown in Figure 4.
Figure 4: Traditional Healthcare Model: Employer, Employees, Insurance, Providers.
Please note the following two key observations in the traditional model
1. Insurance company receives money from employer, employees, and sends some part of money received to the service providers. Insurance company does not inject any money to the system itself.
2. During a year, services received by employees from the providers are not equal.
However, money (premium) paid by an employer and employee is same for all employees. This will cause different amount of profit from different employees.
From observation #2 above, I derive a relationship between Medical Benefit Expense (MBE) and Profit generated by an insurance company from an individual member [12]. Formally, I establish the following relation:
F3(A)+P(A)=F3(B)+P(B)=Constant……....Eq (1)
This implies (Medical Benefit Expense for A) + (Profit from A) =Constant
=(1+EWR(A))*F2(A)-{(O(A)+M(A))}....Eq(2)
EWR(A)=F1(A)/F2(A) .......(3)
by definition, where F1(A) is insurance premium payment by the employer and F2(A) is the premium paid by the employee.
The Equation (2) is an important relationship in developing the model for elastic coupon theory for consumer healthcare market [12,13].
The Equation (1) is an important relation between profit/member and medical benefit expense per member. Based on this equation, I present the following theorem:
Theorem: For every member A in the system (insurance company+service providers+members, existing and potential ), there exists a "pairing" member B, which will allow the combined profit derived from both A and B to be equal to any "feasible" target profit/member set by the insurance company.
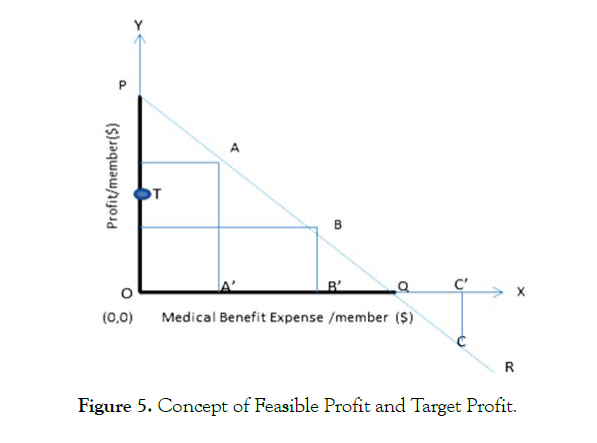
Now, I shall examine the notion of "feasible" profit and "feasible" target profit per member from the geometrical representation as shown below (Figure 5).
Figure 5: Concept of Feasible Profit and Target Profit.
X axis represents Medical Benefit Expense per member and Y axis is Profit/member. The straight line PQR represents the Equation 1. OP represents the maximum profit per member, P(MAX). OQ represents the amount of Medical Benefit Expense (MBE) at which the profit/member becomes zero. If MBE becomes greater than OQ, then insurance company encounters financial loss from that member. Any point on segment OP represents feasible profit per member. A, B and C represent three members in the system. A and B generate profit for the insurance company and member C is causing loss. OP equals to OQ from Equation 1.
In the figure, T represents a feasible target profit; T could lie anywhere in between O and P. If we are given a member, say A, and the target profit (feasible is implied) point T, how can we determine the "pairing" member who will allow the combined profit of A and B equals to T?
Geometrical construction to determine the pairing member: Extend OT to double its length; then subtract AA' (which represents the profit from A). Then draw a horizontal line, the intersection of the horizontal line and line PQR will indicate location of pairing member B.
The algebraic proof is the following:
(P(A)+P(B))/2 =Target profit=T
So, P(B)=2*T–P(A)………Eq. 4
By definition,
P(B
Therefore, 2 * T–P(A)
Or Target Profit, T < (0.5) *( P(A) + P(MAX))
This is the upper bound for Target profit.
An Algorithm for Identification of Pairing Members
The method that I have applied to prove the existence of pairing members is not practical to use for identifying pairing members in an insurance company’s database due to the fact different employers pay different premium (f2) and EWR shall vary from employer to employer. Therefore, if we adopt the above method, we will have different constants, as shown in Equation (1), for different employers. Further, employers may change their contributions to employees’ healthcare plan annually. Then we have to perform the identification process again. To address these problems, I would like to propose an innovative method for identifying pairing members by using the distribution of MBE of the members.
Following is the assumption in developing the proposed methodology.
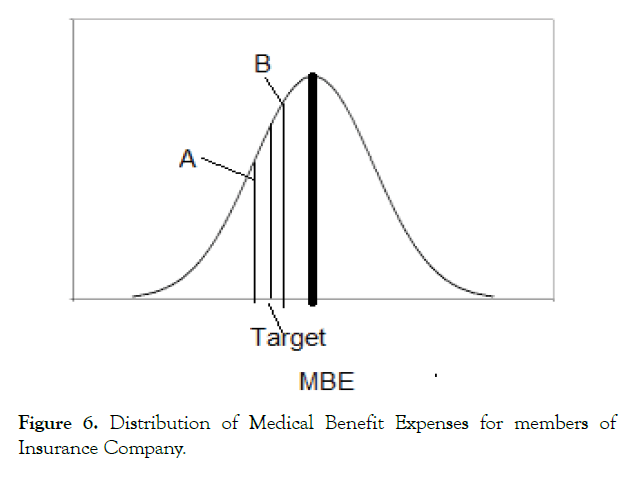
The distribution of Medical Benefit Expense (MBE) for members of a health insurance company is a normal distribution. If the distribution is not a normal distribution, the algorithm can be applied with certain modifications (Figure 6).
Figure 6: Distribution of Medical Benefit Expenses for members of Insurance Company.
The MBE distribution for members in an insurance company is shown in Fig. 6 above. The distribution has a population mean MBEavg as shown by the thick line at the center of the graph.
However, the insurance company would like to select members such that the average MBE of the selected members will be MBETarget which is lower than the MBEavg.
Let us assume A is a member of the selected group with MBE of F3(A), and
F3(A)< MBETarget. …………… Equation (5)
Our objective is to identify the pairing member B such that
F3(A)+F3(B)=2*MBETarget …………… Equation (6)
We would like to formalize the above problem for a more general case.
Let us assume there are N members represented by x1, x2, x3 ………. xN in the subgroup with a target MBETarget.
The actual MBE of member xi is denoted by F3(xi) which could be found from the past observations. The estimated MBE of member xi is represented by F3e (xi) which could be determined by applying some statistical method.
Further, let us assume L is an ascended order list of estimated MBEs.
So, we can represent L = {F3e(x1), F3e(x2), ……F3e(xi), F3e(xi+1 ),……. F3e(xN) } ………Equation (7)
Such that;
F3e(xi+1)>F3e(xi) for i= 1 to N–1 … …. Equation (8)
Given F3e(xi), our goal is to identify its pairing member in the subgroup.
The first step is to calculate the distance of member xi from the target MBE.
STEP 1: We calculate delta (xi) = MBETarget–F3e (xi) Equation (9)
Therefore, F3e(xi) = MBETarget–delta(xi) ………….. Equation (10)
Then our objective will be to find j such that
F3e(xj)=MBETarget+delta (xi) …….. Equation (11)
Please note, the suffix of x in delta in Equation (11) is i.
Following is the pseudo code for the proposed algorithm:
For i=1 to N do {
F3e(i) → Current MBE
Delta (i)=MBETarget–F3e(i)
MBEPairing-member = MBETarget+Delta (i)
While ((MBEPairing-member>F3e(i+1) ). AND. ( F3e (i+1). NOT PAIRED))
/*move to next MBE*/
i= i+1;
j=i-1; /*j is location of pair */
Mark (i,j) as pair
End While
} */End For loop */
A Peer to Peer Network for Healthcare Payment Method
A. A Framework for P2P Payment Method
Symbols used in P2P payment algorithm:
D(i)=i-th Donor/Payor (Employer)
P(i)=j-th Patient (Employee)
V(k)=k-th Provider
X(i,j)=Monthly membership by D(i) to P(j)
S(j,k)=Monthly service fee by P(j) to V(k)
B. Single Payer
As shown in Figure 7, a single patient should be able to meet his/ her obligation to the provider, if monthly service fee S(j,k)<X(i,j).
Figure 7: Single patient to single provider.
The residual membership fee, X(i,j)–S (j,k) is stored as reservoir R(j)
C. Multiple Payers
If S(j,k) > X(i,j) then P(i) first looks for its pairing member P(i’). If the pairing member cannot meet the demand, then P(i) looks for community help (Figure 8).
Figure 8: Pairing member contributes to a single service provider to meet the obligation.
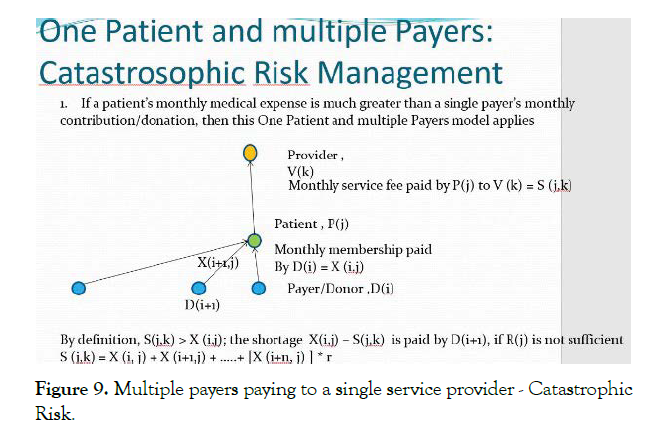
Catastrophic Risk Management Case (Figure 9).
Figure 9: Multiple payers paying to a single service provider - Catastrophic Risk.
Moral Hazard (Figure 10).
Figure 10: Managing Moral Hazard.
System Stability (Figure 11).
Figure 11: System Stability.
Monte Carlo Simulation of Medical Benefit Expenses (MBE) and Pairing Members Identification
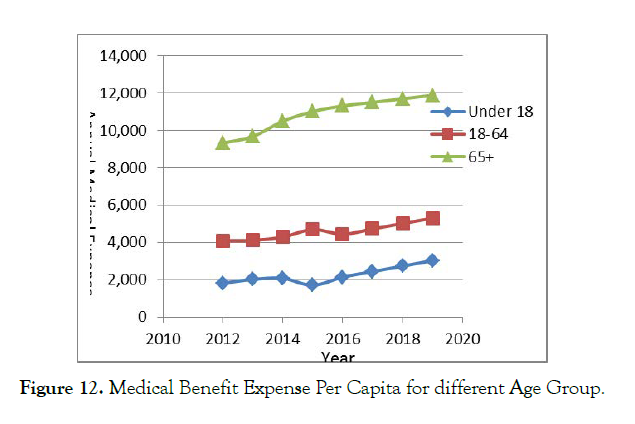
As shown in Figure 12, the Medical Benefit Expense per Capita for different age group in USA has risen during 2010-2019 [14].
Figure 12: Medical Benefit Expense Per Capita for different Age Group.
In order to test the effectiveness of the proposed methodology based on Pairing Members (PM), I used Monte Carlo simulation technique by generating random numbers in Microsoft Excel.
In specific, I used the NORMINV function to generate MBEs with a given expected average and a standard deviation (Tables 1 and 2) [15].
| LOW RISK | Age 0-18 years |
|---|---|
| Average Expense | $ 251.92 |
| Standard Deviation | $ 100.00 |
| Member Monthly Payment | $ 250.00 |
Table 1. Average Expense, Standard Deviation, and Monthly Payment.
| Monthly Medical Expense | Monthly Premium | (Premium - MBE) |
|---|---|---|
| $ 357.17 | $ 250.00 | -$ 107.17 |
| $ 112.31 | $ 250.00 | $ 137.69 |
| $ 330.59 | $ 250.00 | -$ 80.59 |
| $ 356.27 | $ 250.00 | -$ 106.27 |
| $ 306.02 | $ 250.00 | -$ 56.02 |
| $ 179.47 | $ 250.00 | $ 70.53 |
| $ 362.29 | $ 250.00 | -$ 112.29 |
| $ 73.92 | $ 250.00 | $ 176.08 |
| $ 254.03 | $ 250.00 | -$ 4.03 |
| $ 260.93 | $ 250.00 | -$ 10.93 |
| $ 232.91 | $ 250.00 | $ 17.09 |
| $ 533.27 | $ 250.00 | -$ 283.27 |
| $ 279.91 | $ 250.00 | -$ 29.91 |
| $ 53.61 | $ 250.00 | $ 196.39 |
| $ 390.07 | $ 250.00 | -$ 140.07 |
| $ 339.04 | $ 250.00 | -$ 89.04 |
| $ 270.92 | $ 250.00 | -$ 20.92 |
| $ 131.92 | $ 250.00 | $ 118.08 |
| $ 477.49 | $ 250.00 | -$ 227.49 |
| $ 150.56 | $ 250.00 | $ 99.44 |
| $ 248.52 | $ 250.00 | $ 1.48 |
| $ 359.58 | $ 250.00 | -$ 109.58 |
Table 2. List of MBEs for twenty two children generated by Monte Carlo Simulation.
Application of Pairing Members (PM) Methodology
Following is the list of simulated MBEs for twenty two children by method explained above (Table 3).
| Estimated MBE | Patient ID |
|---|---|
| $ 190.46 | 1 |
| $ 416.92 | 2 |
| $ 152.28 | 3 |
| $ 326.86 | 4 |
| $ 41.07 | 5 |
| $ 246.92 | 6 |
| $ 403.96 | 7 |
| $ 350.78 | 8 |
| $ 228.16 | 9 |
| $ 341.18 | 10 |
| $ 468.82 | 11 |
| $ 411.74 | 12 |
| $ 108.88 | 13 |
| $ 262.42 | 14 |
| $ 151.98 | 15 |
| $ 113.65 | 16 |
| $ 286.78 | 17 |
| $ 277.48 | 18 |
| $ 286.47 | 19 |
| $ 238.41 | 20 |
| $ 305.59 | 21 |
| $ 439.57 | 22 |
Table 3. List of MBEs for twenty two young patients.
Step 2: Sorting of the simulated list (Tables 4-6).
| Patient ID | Estimated MBE |
|---|---|
| 5 | $ 41.07 |
| 13 | $ 108.88 |
| 16 | $ 113.65 |
| 15 | $ 151.98 |
| 3 | $ 152.28 |
| 1 | $ 190.46 |
| 9 | $ 228.16 |
| 20 | $ 238.41 |
| 6 | $ 246.92 |
| 14 | $ 262.42 |
| 18 | $ 277.48 |
| 19 | $ 286.47 |
| 17 | $ 286.78 |
| 21 | $ 305.59 |
| 4 | $ 326.86 |
| 10 | $ 341.18 |
| 8 | $ 350.78 |
| 7 | $ 403.96 |
| 12 | $ 411.74 |
| 2 | $ 416.92 |
| 22 | $ 439.57 |
| 11 | $ 468.82 |
Table 4. Sorted List.
| Target MBE = $300 | ||
| Pick | 17, 21 | 296.1816 |
| Pick | 4, 19 | 306.6648 |
| Pick | 10, 18 | 302.169 |
| Pick | 8, 14 | 306.5975 |
| Pick | 7, 6 | 325.4419 |
| Pick | 12, 20 | 325.0744 |
| Pick | 2,9 | 322.5426 |
| Pick | 22, 1 | 315.0135 |
| Pick | 11, 3 | 310.5512 |
Table 5. Pairing of members.
| Difference from the Target | |
|---|---|
| -3.818375 | |
| 6.664776 | |
| 2.169009 | |
| 6.597526 | |
| 25.44189 | << |
| 25.07438 | << |
| 22.54261 | << |
| 15.0135 | <<< |
| 10.55122 | <<< |
Table 6. Calculation of difference from the target for each pair in the first round of pairing.
Conclusions
In this paper, it is proven that pairing members in a P2P network should be able to balance the payments to medical service providers.
Future work should be directed towards design and construction of the P2P Network for a test group of patients and service providers. We plan to use Distributed Ledger Technology (DLT) to implement Blockchian method to ensure accuracy and integration of payment transactions.
REFERENCES
- OECD. Health at a Glance - OECD Indicators. 2017.
- Cutler D, Richardson E. Your Money and Your Life: The Value of Health and What Affects It. Front Health Pol Res. 1999;2:99-132.
- Brook RH. The Role of Physicians in Controlling Medical Care Costs and Reducing Waste. American Medical Association, 2011;306:650-651.
- Newsom M, Fernandez B. Private Health Insurance Premiums and Rate. 2011.
- Collins SR, Radley DC. The Cost of Employer Insurance Is a Growing Burden for Middle-Income Families. 2018.
- Bose A. A Peer to Peer Healthcare Payment Platform. Cornell University. 2020.
- Grones G. Top 10 health insurance companies in the US. 2020.
- Feldstein PJ. National Health Insurance: Which Approach and Why? Health Pol Iss. 2019;36:585-602.
- Schollmeier R. A Definition of Peer-to-Peer Networking for the Classification of Peer-to-Peer Architectures and Applications. 2001.
- Andriopoulou FG, Birkos KD, Lymberopoulos DK. P2Care: A Dynamic Self-Organized Healthcare Network for Ubiquitous Healthcare Environment. 2013.
- Pirahandeh M, Kim D. Co-Designing an Intelligent Doctors-Colleagues-Patients Social Network. 2012.
- Bose A. Application of Generalized Elastic Coupon model in US Healthcare market and Development of "Pairing" Members Theorem.2018.
- Bose A. Data distribution database and method for data distribution and verification. US Patent. 2013.
- Agency for HealthCare Research and Quality. 2019.
- Bose A. Monte Carlo Simulator for Medical Benefit Expenses. 2020.
Citation: Bose A (2020) Healthcare without Health Insurance: A Peer to Peer Healthcare Payment Platform. Health Care Services 8: 257. doi: 10.35248/2375-4273.20.8.257
Copyright: © 2020 Bose A. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.