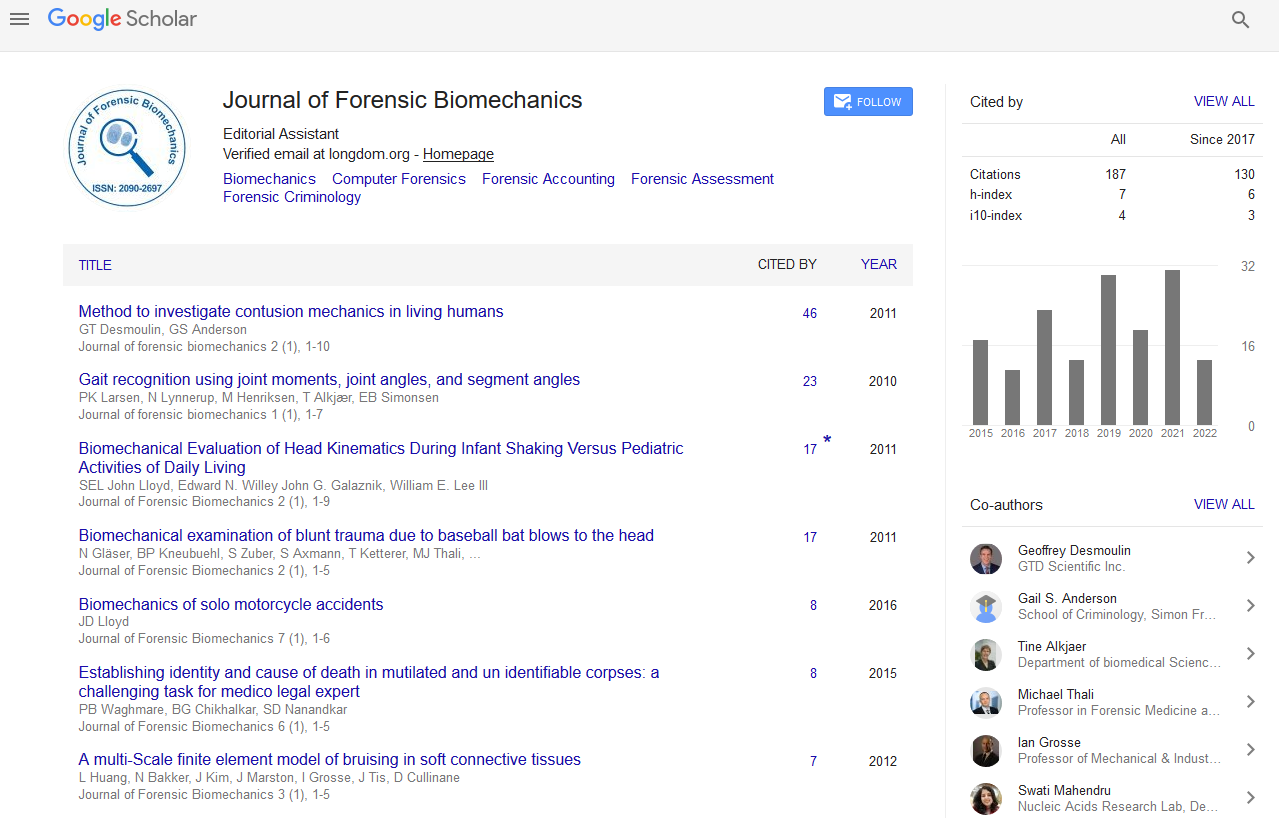
Indexed In
- Genamics JournalSeek
- SafetyLit
- Ulrich's Periodicals Directory
- RefSeek
- Hamdard University
- EBSCO A-Z
- Geneva Foundation for Medical Education and Research
- Euro Pub
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Research Article - (2022) Volume 13, Issue 6
Handcuff Pressure and Risk of Superficial Radial Nerve Injury
Geoffrey T Desmoulin1*, Olivia Hetland1, Benjamin W Hollins1 and Theodore E Milner1,22Department of Kinesiology and Physical Education, McGill University, Montreal, Canada
Received: 15-Oct-2022, Manuscript No. JFB-22-18378; Editor assigned: 19-Oct-2022, Pre QC No. JFB-22-18378 (PQ); Reviewed: 02-Nov-2022, QC No. JFB-22-18378; Revised: 10-Dec-2022, Manuscript No. JFB-22-18378 (R); Published: 18-Nov-2022, DOI: 10.35248/2090-2697.22.13.410
Abstract
Background: A number of cases of handcuff neuropathy have been reported in the literature. Specifically, when handcuffs remain fastened around the wrists for a prolonged period there is a risk that function of the superficial radial nerve can be compromised. Although cases of median and ulnar nerve injury have also been reported, they are much less frequent and are usually accompanied by injury to the superficial radial nerve.
Methods: We hypothesized that the pressure applied to the superficial radial nerve by tightened handcuffs could readily exceed nerve injury thresholds. To test our hypothesis, we created a physical model of the wrist and superficial radial nerve which allowed us to measure the pressure applied by tightened handcuffs. We tested two handcuff designs and compared the measured pressures to pressures known to produce loss of function of the rat tibial nerve, a nerve which is similar in diameter to the human superficial radial nerve.
Findings: We found that relatively low levels of force applied by tightened handcuffs can produce pressures which exceed nerve injury thresholds if sustained for sufficiently long time periods.
Interpretation: Our results suggest that precautions must be taken by law enforcement officers, when fastening handcuffs, to ensure that the force produced by tightened handcuffs remains below nerve injury thresholds, that the double locking mechanism is engaged and that detainees should be made aware that movements which increase the force applied to the superficial radial nerve, even periodically, can increase the risk of nerve injury.
Keywords
Handcuffs; Superficial radial nerve; Neuropathy; Physical models
INTRODUCTION
Neuropathy of the superficial radial nerve can occur when the nerve is compressed during procedures involving fastening of handcuffs around the wrists. Handcuffs are typically fastened between the base of the thumb and the distal end of the radius and between the pisiform bone and the distal end of the ulna. Since the superficial radial nerve passes across the gap between the distal end of the radius and the base of the thumb, it is subject to compression when the strands of a handcuff are tightened. A number of studies have documented neuropathy which can be attributed to prolonged handcuff pressure [1-9]. Although the ulnar and/or median nerve may also be affected, such instances are less common and are more likely the result of pressure caused by subsequent swelling of the wrist rather than the initial handcuff tightness [3,5-8].
Several studies have examined the neuropathic effects of prolonged pressure or force applied to a peripheral nerve and can, therefore, serve to establish thresholds for the risk of loss of superficial radial nerve function due to prolonged handcuff pressure. Szabo and Sharkey used the rat tibal nerve to model repetitive work-related nerve injury in humans by applying constant pressure of 30, 60 or 90 mm Hg to the nerve and measuring the compound action potential amplitude at 15 min intervals [10]. The rat tibial nerve is a good model for the human superficial radial nerve because it has a similar diameter [11,12]. Szabo and Sharkey found that constant pressure of 60 or 90 mm Hg resulted in a 50% reduction in nerve function after 1 h and complete loss of nerve function after 2.5 h [10]. Even constant pressure of 30 mm Hg reduced nerve function by 50% after 3.25 h. They also investigated the effect of 1 Hz cyclical variation in pressure between 0 to 30 mm Hg, 20 to 50 mm Hg and 30 to 60 mm Hg. Although there was relatively little loss of nerve function for the 0 to 30 mm Hg cycle, nerve function was reduced by 50% after 3 h for the 20 to 50 mm Hg cycle and complete loss of function after 4.5 h for the 30 to 60 mm Hg cycle.
Yoshii et al. investigated the effect of prolonged constant pressure of 40, 80 or 120 mm Hg on the function of rabbit sciatic nerve, which is approximately 3 mm in diameter [13,14]. Although 40 mm Hg produced no change in compound action potential amplitude after 30 min, applied pressures of 80 and 120 mm Hg resulted in approximately 20% and 30% declines in nerve function, respectively. When the nerve was allowed to recover by releasing pressure, compound action potential amplitude returned to within 5% of its pre-compression value after applied pressure of 80 mm Hg after 30 min, but remained almost 20% below its pre-compression value after applied pressure of 120 mm Hg.
Changes to handcuff design have been relatively minor over the past century. The basic design comprises double and singles semicircular strands which interlocks and tighten by engaging a ratchet mechanism. Once interlocked, the ratchet can be advanced to tighten the strands. However, the ratchet cannot be reversed, preventing the strands from loosening unless the strands are unlocked with a key. Once adequately tightened, the strands are normally locked in place by setting a pin, referred to as a doublelock, to prevent further tightening. Failure to set the double-lock, allows the ratchet to slip and risks additional tightening. Thus, pressure on the superficial radial nerve may arise from the initial tightening of the strands or from slipping of the ratchet if the double-lock is not engaged.
Given some recent changes to handcuff design, notably in the contour and smoothness of the strands, we determined to compare the risk of loss of superficial radial nerve function due to prolonged handcuff pressure with different handcuff designs. We hypothesized that the pressure applied to the superficial radial nerve by tightened handcuffs could readily exceed nerve injury thresholds and that strand smoothness would not modify the risk of neuropathy since the internal pressure would be related directly to the magnitude of the load. To test our hypothesis, we created models of the wrist with a fluid filled flexible tube positioned at the location of the superficial radial nerve. The tube served as a surrogate nerve and allowed us to measure the internal pressure when the handcuff was tightened or when a constant force was applied.
Methodology
Apparatus
Physical models were constructed to represent the wrist of a female and male, based on anthropometric data [15]. Each model consisted of two wooden dowels joined with a bolt, to simulate the radius and ulna. In addition to stabilizing the dowels, the bolt permitted adjustment of the separation distance. Dowels of 3.175 cm diameter, separated to create a width of 7 cm, were used to model the wrist of a male. Dowels of 2.54 cm diameter, separated to create a width of 5.5 cm, were used to model the wrist of a female. The wrist width, rather than the wrist thickness, was considered to be the critical dimension, since the relatively circular shape of the handcuff strands dictates that the pressure points are at the lateral and medial margins of the wrist, i.e. the wrist width is greater than its thickness. A silicone tube with an inside diameter of 1 mm and outside diameter of 2 mm was taped along the side of one of the dowels to serve as a surrogate for the superficial radial nerve (Figure 1). A small foam pad, approximately 5 mm thick was placed over the tube to ensure that the handcuff would not pinch off the tube as it was tightened or loaded. The tube was filled with mineral oil and connected to a pressure sensor (Focket 30 PSI, China). The mineral oil was pressurized by means of a syringe attached to a valve connected to the tube (Figure 1) prior to testing, such that all measurements were made as increases in pressure relative to the baseline of the pressurized tube. A series of tests were conducted at different baseline pressure levels which established that the change in tube pressure, produced by repeatedly applying the same load to the tube, did not vary with baseline pressure, i.e., there was a fixed relation between load and change in tube pressure. Therefore, no attempt was made to maintain the same baseline pressure during testing.

Figure 1: A) Handcuff models used in tests. B) Test setup for handcuff tightness tests showing wrist model, comprising wooden dowels and pressurized tube. C) Setup for handcuff loading tests showing cable from which weights were hung to apply pressure to the tube.
Two handcuff designs were compared (Figure 1A). One design was a standard design used by the majority of manufacturers. The model which was tested was the Smith and Wesson M-100. The second design involves a modification to the strand shape, creating a more oval contour and a smoother edge. The model which was tested was the ASP Ultra Plus.
Protocol
Three basic tests were performed to determine the tube pressure created by tightening or loading the handcuff. The first test involved incrementally increasing the handcuff tightness by one ratchet tooth until pressure first rose above baseline. Tube pressure measurements were then made for each additional advance of the ratchet, until the ratchet could not be advanced to the next tooth, i.e., the tightness limit had been reached. During this test, the dowels were clamped to a countertop using C-clamps (Figure 1B). Between each measurement, the handcuff was loosened. Tube pressure was measured continuously over a 4 s interval, beginning when the handcuff was loose and ending after the ratchet had been advanced to the desired tightness (Figure 2).

Figure 2: Tube pressure record during tightening of handcuff. Applied pressure was calculated as the difference between the mean pressure over the first 100 ms, prior to tightening the handcuff, and the mean pressure over final 500 ms, after the handcuffs had been tightened and pressure had stabilized, indicated by the vertical dashed lines. The difference in pressure for the record shown in the plot was 113 mm Hg.
The second test involved loading the handcuff with a series of weights. In this test the dowels were clamped in a vise so that the tube could be loaded vertically through the gravitational force applied by the weights (Figure 1C). In one condition, the dowels were oriented horizontally so that the load was applied perpendicular to the tube. In a second condition, the dowels were inclined downward at a 30° angle to create a slight tilt to the handcuff strands so that the load would be applied more along the edge of the strand rather than the center of the strand. The handcuff strands were engaged but loose such that pressure was applied to the tube by adding weight rather than by tightening the handcuff. A cable was passed through a handcuff link and weights were attached to the cable such that the handcuff applied pressure to the tube (Figure 1C). The weights produced forces of 10.57 N, 20.65 N, 30.59 N, 41.75 N, 51.72 N and 62.41 N. Tube pressure was measured continuously from before the weight was attached to the cable until the weight was hanging in a steady state over a 10 s interval.
In the third test, like the second, the handcuff strands were engaged but loose and the dowels were oriented horizontally. The handcuff was loaded with the 20.65 N weights then tilted and released, allowing it to rock back and forth without intervention for two cycles. This test was only performed with the male wrist model and was designed to simulate the variation in pressure when a detainee twisted the handcuffs. The test focused on the variation in tube pressure during oscillations rather than the steady state pressure for a constant load. Tube pressure was again measured continuously, beginning prior to the initial tilting of the handcuff and continuing until the completion of two oscillations.
Data acquisition
Tube pressure was acquired at a sample rate of 1000 Hz. All pressures are reported in mm Hg to allow for comparison with the animal studies on isolated nerves [10,13,16]. The first two tests were repeated 5 times and the third test was repeated 10 times. Prior to analysis, the pressure signal was digitally low-pass filtered using a fifth-order Butterworth filter with a cutoff frequency of 10 Hz, implemented in Matlab.
Analysis
For the first two tests, baseline tube pressure was computed as the average pressure during a 100 ms interval prior to tightening or loading the handcuff. Final steady state tube pressure after tightening or loading was computed as the average tube pressure during the final 500 ms of the sampling period (Figure 2). The mean and standard deviation of the change in tube pressure relative to baseline of the 5 trials for each condition were then computed. For loading tests, linear regression was also performed for the mean change in tube pressure relative to baseline as a function of load force. The slopes and intercepts for the two handcuff designs and the two wrist models were compared using a two-sided Student’s t-test.
For the third test, the handcuff was preloaded with the 20.65 N weights prior to the onset of recording. Baseline pressure was computed as the average pressure during a 100 ms interval prior to tilting the handcuff. Thus, it represented the pressure with the 20.65 N loads, rather than the unloaded tube pressure. The difference between the baseline and the average of the 3 tube pressure peaks were recorded for each trial (Figure 3). The values for the 10 trials conducted with each of the two handcuff designs were then compared using a two-sided Student’s t-test.

Figure 3: Tube pressure record during rocking motion after titling the handcuff when loaded with 20.65 N weights. Change in pressure was measured relative to mean pressure over 100 ms interval prior too tilting the handcuff, shown by dashed vertical lines. Dashed horizontal lines indicate pressure peaks during rocking, which were averaged to quantify the effect of twisting the handcuff.
Results
We found that the ratchet mechanism could only be advanced by one or two increments from the tightness at which tube pressure first began to increase above baseline until the handcuff was so tight that the ratchet could no longer be advanced by an additional increment. The mean recorded changes in tube pressure, relative to baseline (loose handcuff) for all handcuff tightness tests are shown in Figure 4. The strands of the Smith and Wesson handcuff had a smaller aperture than the ASP handcuff. Consequently, tightness limits were reached at 3 fewer ratchet increments than for the ASP handcuffs, for both the female and male wrist models. For both male and female wrist models with the ASP handcuffs and for the female wrist model with the Smith and Wesson handcuffs, it was possible to advance the ratchet by two increments beyond the strand position for which tube pressure first began to increase. In these cases, the increase in tube pressure was greater for the second increment than the first increment. In all cases, the mean tube pressure exceeded 30 mm Hg at the final ratchet increment and in 3 of the 4 cases it exceeded 60 mm Hg.

Figure 4: Mean and standard deviation of tube pressure created by tightening handcuffs. Numbers of handcuff strand ratchet increments relative to loose handcuffs are indicated on the horizontal axis. Left panels show results for Smith and Wesson handcuffs for the two wrist models and right panels show results for ASP handcuffs.
The fixed distance between adjacent ratchet teeth and the small number of ratchet increments between the minimum and maximum tightness that could be tested, limited the amount of information that could be derived. Furthermore, the tightness did not appear to be comparable for the two handcuff designs. To better compare the effect of handcuff design on nerve pressure, it was decided to load each handcuff with a series of weights from which a general relation could be derived between tube pressure and force applied by the handcuff. The relations between applied force and the tube pressure for the two handcuff designs and wrist models are shown in Figure 5. The relations are very similar. A statistical comparison was made between the handcuff designs and wrist models by computing linear regression coefficients, i.e. slope and intercept, for each handcuff design and wrist model and performing a two- sided Student’s t-test. The regression coefficients are listed in Table 1. No significant differences in the slopes or intercepts were found between the linear relations for the two handcuff designs for either the male or female wrist models.
| Orientation | Wrist model | Handcuff | Slope | Standard error | p-value | Intercept | Standard error | p-value |
|---|---|---|---|---|---|---|---|---|
| Horizontal | Female | ASP | 10.39 | 2.5 | 0.437 | 39.7 | 22.6 | 0.438 |
| S&W | 10.92 | 2.17 | 10.9 | 16.7 | ||||
| Horizontal | Male | ASP | 12.29 | 0.52 | 0.152 | 6.9 | 5.1 | 0.48 |
| S&W | 12.16 | 2.46 | 11 | 24.2 | ||||
| 30° | Female | ASP | 15.13 | 1.22 | 0.164 | 0.9 | 11.1 | 0.082 |
| S&W | 13.23 | 1.36 | 26.2 | 12.3 | ||||
| 30° | Male | ASP | 6.53 | 1.98 | 0.152 | 74 | 17.9 | 0.154 |
| S&W | 9.86 | 2.3 | 46 | 20.9 |
Table 1: Linear regression, pressure vs. force.

Figure 5: Comparison of tube pressure for loads applied to wrist models oriented horizontally. Mean pressure applied by Smith and Wesson handcuffs shown by triangles. Mean pressure applied by ASP handcuffs shown by circles. Error bars indicated standard deviation.
Given that the strands of the ASP handcuffs had a more rounded edge than the Smith and Wesson handcuffs, an additional test was conducted with the wrist models inclined at an angle of 30° with respect to horizontal such that the load was applied more towards the edge of the handcuff strand. The resulting relations between applied force and tube pressure are shown in Figure 6. Linear regression analysis again indicated that there was no statistically significant difference in the slopes of intercepts for the two handcuff designs.

Figure 6: Comparison of tube pressure for loads applied to wrist models oriented at 30° relative to horizontal. Mean pressure applied by Smith and Wesson handcuffs shown by triangles. Mean pressure applied by ASP handcuffs shown by circles. Error bars indicated standard deviation.
One final test was performed to simulate the effect of intermittently twisting the handcuffs during which the load would be expected to increase and decrease and the angle of the handcuff strand changed relative to the surface of the wrist. During these tests the handcuff was loaded with a weight of 20.65 N, tilted relative to the horizontal then released and allowed to oscillate on its own. The resulting change in tube pressure is shown in Figure 3. The tube pressure increased as the handcuff was tilted and then oscillated with decreasing amplitude for two cycles until the oscillation ended. For the 10 trials, the mean increase in peak tube pressure, relative to baseline, during the oscillations was 48.7 ± 2.3 mm Hg for the Smith and Wesson handcuffs and 45.4 ± 7.5 mm Hg for the ASP handcuffs. The values were not significantly different for the two handcuff designs.
Discussion
The objectives of our study were to determine the risk of injury to the superficial radial nerve posed by pressure applied to the nerve when handcuffs are fastened and manipulated and whether the design of the handcuff strands can affect the risk. Models for a male and a female wrist were constructed with a pressurized tube, of similar diameter to the nerve, placed in a position simulating the anatomical location of the superficial nerve relative to the radius. The results indicate that relatively low handcuff forces produce pressures which exceed thresholds for neuropathy if applied for prolonged periods and that handcuff strand design has little effect on the risk of nerve injury.
Numerous reports have documented the incidence of injury to the superficial radial nerve when handcuffs are clamped around the wrist over a prolonged period [1-9]. However, there has been no systematic investigation of the relation between force applied by handcuffs and the risk of injury to the superficial radial nerve. We assumed that the threshold for injury would be similar to that of the rat tibial nerve, which is similar in diameter to the human superficial radial nerve. Showed that constant pressure, as low as 30 mm Hg, applied to the rat tibial nerve could lead to a 50% decline in nerve function if applied for 3.25 h and that pressures of 60 and 90 mm Hg could lead to 50% loss of nerve function after 1 h. Studies conducted with the rabbit sciatic nerve suggested that higher pressures were required to produce similar loss of nerve function [13]. However, the rabbit sciatic nerve is approximately twice the diameter of the human superficial radial nerve and, therefore, has a more extensive intraneural vasculature, which would reduce its susceptibility to nerve injury [16]. Examined intraneural blood flow when pressure was applied to rabbit tibial nerves and found that compression of 20 to 30 mm Hg retarded venular blood flow. At 60 mm Hg there was complete ischemia of the compressed nerve segment in 9 of 15 nerves, and 70 mm Hg caused ischemia in all nerves but one, which was ischemic when compressed at 80 mm Hg. Thus, loss of nerve function due to prolonged pressure application is likely due to compromised intraneural blood flow.
Tube pressures of 60 mm Hg or greater were achieved at maximum handcuff tightness for both handcuff designs on the male wrist model and for one of the handcuff designs on the female wrist model, suggesting that tightening the handcuffs maximally would produce significant loss of superficial radial nerve function within an hour. Although general policies regarding detention in handcuffs dictate that handcuffs be removed within one hour, nerve damage could still occur within that time frame if the pressure is sufficiently high. Furthermore, situations arise in which detainees are restrained in handcuffs for periods exceeding one hour.
However, there were limitations to the initial tests of handcuff tightness, given that there was no objective measure of tightness and the pressure varied, depending on the size of the wrist model. Therefore, the tightness tests could not be generalized to an arbitrary wrist size. To circumvent this limitation, tests were conducted in which the load was controlled and the same load was applied with each handcuff design and each wrist model. When the load was controlled, no significant difference was found in the relation between applied force and tube pressure, which suggests that pressure applied to the superficial radial nerve by a handcuff, depends almost exclusively on handcuff tightness and that the shape of the handcuff strand is not a consequential factor.
All tests with controlled loads, demonstrated that loads above 20 N, a relatively small force, produced tube pressures greater than 60 mm Hg. In tests conducted with a male and female subject, we found that 20 N was approximately 20% of the maximum force which the female subject could produce and 10% of the maximum force which the male subject could produce when attempting to pull the wrists apart while handcuffed. Thus, there is a significant risk that even slightly over tightened handcuffs could produce superficial radial neuropathy if maintained over a prolonged period.
We found that simple rocking motion of the handcuff strand could increase tube pressure by over 45 mm Hg. Therefore, even if handcuffs produce no pressure on the superficial radial nerve when initially clamped around a detainee’s wrists, the pressure could increase above 45 mm Hg if the detainee attempts to twist the wrists in the handcuffs. Showed that cyclical compression of the rat tibial nerve between 0 and 30 mm Hg could produce 20% loss of nerve function after 3 h [10]. However, cyclical pressure between 20 and 50 mm Hg produced similar loss of nerve function after slightly more than 1 h and after less than 1 h for cyclical compression between 30 and 60 mm Hg. When prolonged for 3 h, cyclical compression between 20 and 50 mm Hg produced approximately 50% loss of nerve function, whereas cyclical compression between 30 and 60 mm Hg produced over 80% loss of nerve function.
Conclusion
Although over tightened handcuffs are a definite risk factor for superficial radial nerve injury, manipulation of the handcuffs by a detainee may pose an even greater risk. Given that twisting the wrists inside the handcuffs could produce inadvertent additional tightening of the handcuffs if the double-lock mechanism is not engaged, there is an obligation to ensure that the individual responsible for fastening the handcuffs is trained to appropriately limit the tightness of the handcuffs, e.g. to ensure that a finger can be inserted between the handcuff and the wrist, and that the detainee is made aware of the risk of nerve injury posed by struggling after handcuffs have been fastened around the wrists.
Declaration of Interests
1. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
2. The authors declare the following financial interests/personal relationships which may be considered as potential competing interests.
References
- Smith MS. Handcuff neuropathy. Ann Emerg Med. 1981;10(12):668.
- Levin RA, Felsenthal G. Handcuff neuropathy: Two unusual cases. Arch Phys Med Rehab. 1984;65(1):41-43.
[Google Scholar] [PubMed]
- Richmond PW, Fligelstone LJ, Lewis E. Injuries caused by handcuffs. BMJ. 1988;297(6641):111-112.
[Crossref] [Google Scholar] [PubMed]
- Scott TF, Yager JG, Gross JA. Handcuff neuropathy revisited. Muscle Nerve. 1989;12(3):219-220.
[Crossref] [Google Scholar] [PubMed]
- Stone DA, Laureno R. Handcuff neuropathies. Neurology. 1991;41(1):145-147.
[Crossref] [Google Scholar] [PubMed]
- Satkunam L, Zochodne DW. Bilateral ulnar handcuff neuropathies with segmental conduction block. Muscle Nerve. 1995;18(9):1021-1023.
[Crossref] [Google Scholar] [PubMed]
- Haddad FS, Goddard NJ, Kanvinde RN, Burke F. Complaints of pain after use of handcuffs should not be dismissed. BMJ. 1999;318(7175):55.
[Crossref] [Google Scholar] [PubMed]
- Grant AC, Cook AA. A prospective study of handcuff neuropathies. Muscle Nerve. 2000;23(6):933-938.
[Crossref] [Google Scholar] [PubMed]
- Chariot P, Ragot F, Authier F-J, Questel F, Diamant-Berger O. Focal neurological complications of handcuff application. J Forensic Sci. 2001;46(5):1124-1125.
[Crossref] [Google Scholar] [PubMed]
- Szabo RM, Sharkey NA. Response of peripheral nerve to cyclic compression in a laboratory rat model. Journal Orthop Res. 1993;11(6):828-833.
[Crossref] [Google Scholar] [PubMed]
- Bobkiewicz A, Cwykiel J, Siemionow M. Anatomic variations of brachial and lumbosacral plexus models in different rat strains. Microsurgery. 2017;37(4):327-333.
[Crossref] [Google Scholar] [PubMed]
- Visser LH. High-resolution sonography of the superficial radial nerve with two case reports. Muscle Nerve. 2009;39(3):392-395.
[Crossref] [Google Scholar] [PubMed]
- Yoshii Y, Nishiura Y, Terui N, Hara Y, Saijilafu, Ochiai N. The effects of repetitive compression on nerve conduction and blood flow in the rabbit sciatic nerve. J Hand Surg. 2010;35(4):269-278.
[Crossref] [Google Scholar] [PubMed]
- Shen J, Wang H-Q, Zhou C-P, Liang B-L. Magnetic resonance micro-neurography of rabbit sciatic nerve on a 1.5-T clinical MR system correlated with gross anatomy. Microsurgery. 2008;28(1):32-36.
[Crossref] [Google Scholar] [PubMed]
- Tilley AR. The Measure of Man and Woman: Human Factors in Design. Wiley. 2002.
- Rydevik B, Lundborg G, Bagge U. Effects of graded compression on intraneural blood flow. An in vivo study on rabbit tibial nerve. J Hand Surg Am. 1981;6(1):3-12.
[Crossref] [Google Scholar] [PubMed]
Citation: Desmoulin GT, Hetland O, Hollins BW, Milner TE (2022) Handcuff Pressure and Risk of Superficial Radial Nerve Injury. J Forensic Biomech. 13:410.
Copyright: © 2022 Desmoulin GT, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.