Indexed In
- Open J Gate
- Genamics JournalSeek
- Academic Keys
- JournalTOCs
- ResearchBible
- China National Knowledge Infrastructure (CNKI)
- Scimago
- Ulrich's Periodicals Directory
- Electronic Journals Library
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- SWB online catalog
- Virtual Library of Biology (vifabio)
- Publons
- MIAR
- Scientific Indexing Services (SIS)
- Euro Pub
- Google Scholar
Useful Links
Share This Page
Journal Flyer
Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Research Article - (2021) Volume 12, Issue 3
Effects of Nanoparticles on Non-Darcy Mixed Convective Heat Transfer in Nanofluids over a Shrinking and Stretching Wedge
Hassan Saad Abd Elaal El-dawy1* and Rama Subba Reddy Gorla22Department of Mechanical Engineering, Cleveland State University, Cleveland, USA
Received: 26-Feb-2021 Published: 19-Mar-2021, DOI: 10.35248/2157-7439.21.12.564
Abstract
In this work we studied the effect of nanoparticles on the velocity and heat transfer during the flow of nanofluid in Non- Darcy mixed convection, over a wedge, taking into account of shrinking and stretching of the surface. The governing partial differential equations are converted into ordinary differential equations by means of coordinate transformation. The transformed equations are solved by means of fourth order Runge Kutta method in conjunction with shooting method. The results for the velocity and temperature fields are presented graphically as well as in tabular form. Friction factor decreases with nanoparticle concentration whereas heat transfer rate increases with nanoparticle concentration.
Keywords
Nanoparticle; Nanofluid; Suction; Wedge; Shrinking; Stretching
Introduction
The efficiencies of thermal devices and systems are related to heat transfer rates which in turn depend on the thermal conductivity of the working fluids. Despite considerable previous research and development efforts on heat transfer enhancement, the demand is growing for more efficient and robust heat transfer fluids with significantly higher thermal conductivities than traditional ones. Nanofluids are engineered by suspending nanoparticles with average sizes below 100 nm in traditional heat transfer fluids such as water, oil, and ethylene glycol. Many interesting properties of nanofluids have been reported in the past decades. Nanofluids have better stability because of the larger surface-area-to-volume ratio of nanoparticles which overcome differences in density. Therefore, the exploitation
of nanofluids opens up the possibilities to improve the efficiency of thermal system while maintaining the existing footprint. Alternatively nanofluids can provide the same efficiency of the cooling system at smaller and lighter footprint as reduced inventory of heat transfer fluids. Eventually, improved cooling performance and lower manufacturing or operating cost in thermal system are the major advantage derived from the application of nanofluids.
Owing to this stimulating benefits, a large number of research in the scientific community are being carried out with the goal of realising various applications of nanofluids. Initial research focused mainly on thermal conductivity, only recently that subsequently researchers delved into other area of interest such as viscosity, specific heat, density, critical heat flux, heat transfer coefficient, entropy and wear resistance. In existing experimental works, nanofluids can be produced by two methods, namely the two-step process and the one-step process. In a typical two-step process, the nanoparticles are first produced in dry powder form and then mixed with the heat transfer fluids. However, these nanofluids are not stable even though the stability could be enhanced by pH control and surfactant addition. In the one-step process, the synthesis and dispersion of nanoparticles are done at the same time. These nanofluids have better stability due to the weakened Van der Waals force between nanoparticles. Nevertheless, the twostep process is always preferred by the majority of researchers owing to its low setup cost.
El-dawy et al. analyzed the flow of a nanofluid in the vicinity of stagnation point [1]. Unsteady Flow of a Nanofluid over a Shrinking/Stretching Porous Wedge was studied by El-dawy and Gorla [2]. Chemical reaction effects on non-Darcy mixed convective heat and mass transfer past a porous wedge were studied [3]. Influence of particulate thermophoresis on convection heat and mass transfer was considered by Jize Sui [4]. MHD boundarylayer flow of a micropolar fluid past a flat plate was considered [5]. El-dawy et al. studied the mixed convection in a nanofluid past a vertical plate embedded in a saturated porous medium [6]. Yih analyzed the MHD forced convection flow adjacent to a nonisothermal wedge [7]. Abu-Nada and Oztop studied the effect of inclination angle on natural convection in nanofluids [8]. In this paper, we study the effect of nanoparticles in nanofluids on the surface of a wedge taking into account of shrinking and stretching of the surface.
Mathematical analysis
We consider the steady, laminar mixed convective flow of a nanofluid over a wedge. The density variation and viscosity effects are taken into account in the momentum equation and Boussinesq approximation is made. Let the x-axis be taken along the wedge and the y axis normal to the surface of the wedge. We include suction or injection on the surface of the wedge. The governing equations within boundary layer approximation may be written as:
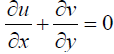 (1)
(1)
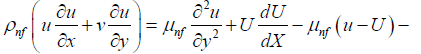
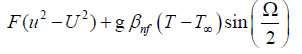 (2)
(2)
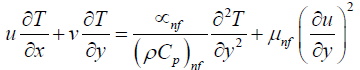 (3)
(3)
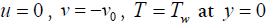 (4)
(4)
where u and v are the velocity components in the x and y directions, respectively, g is the acceleration due to gravity, ρf is the density of the fluid, ρs is the density of the nanoparticle; βnf is the coefficient thermal expansion ; T, Tw, and T∞ are the temperature of the fluid inside the thermal boundary layer, the plate temperature and the fluid temperature in the free stream, respectively; kf is the thermal conductivity of the fluid; ks is the thermal conductivity of the nanoparticle , μnf is the dynamic viscosity; Cpf is the specific heat of the fluid, Cps is the specific heat of the nanoparticle Ω is the angle of inclination of wedge, and F is (Forchheimer number).
Proceeding with the analysis, we define the following transformations:
 (5)
(5)
 (6)
(6)
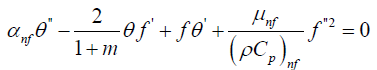 (7)
(7)
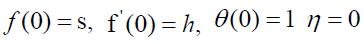
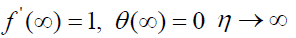 (8)
(8)
Numerical solution
The set of non- linear ordinary Eqs (6) and (7) with boundary conditions (8) have been solved by using the Runge Kutta-Gill method along shooting technique with variables h<0 is shrinking surface, h>0 is sretching surface
Results and Discussion
Demographic characteristics of the study population
The effect of nanoparticle on nanofluids, which, passed over a shrinking and stretching wedge. We see the results appear from the figures. Figure shows the effect of nanoparticle concentration on the velocity distribution within the boundary layer (Figure 1). We see from Figure 1 that as the nanoparticle concentration increases, in each case stretching and shrinking, the velocity decreases. Figure shows the effect of nanoparticle concentration on the temperature distribution within the boundary layer (Figure 2). We see from Figure 2 that as the nanoparticle concentration increases, in each case stretching and shrinking, the temperature increases.
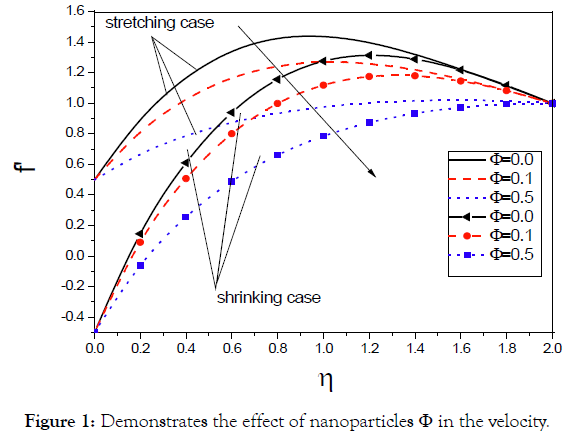
Figure 1: Demonstrates the effect of nanoparticles Φ in the velocity.
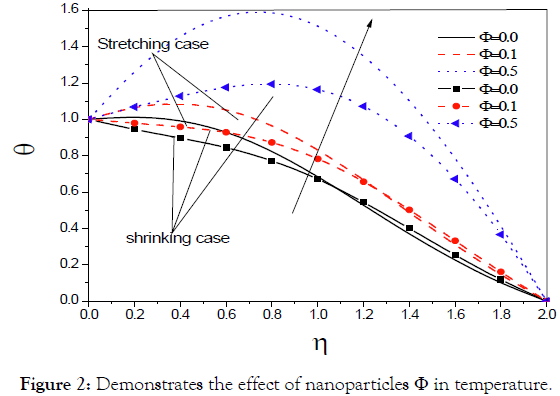
Figure 2: Demonstrates the effect of nanoparticles Φ in temperature.
Figure shows that as the suction parameter increases in each case, stretching and shrinking, the velocity increases (Figure 3). Figure shows that as the suction parameter increases in each case, stretching and shrinking, the temperature decreases (Figure 4). Figure shows the effect of wedge angle on velocity distribution (Figure 5). We notice that as the wedge angle increases, in each case stretching and shrinking, the velocity decreases. Figure shows the effect of wedge angle on temperature distribution (Figure 6). We notice that as the wedge angle increases, in each case stretching and shrinking, the temperature decreases.
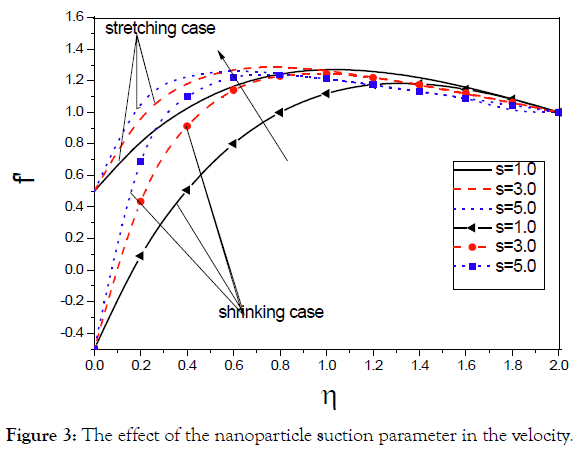
Figure 3: The effect of the nanoparticle suction parameter in the velocity.
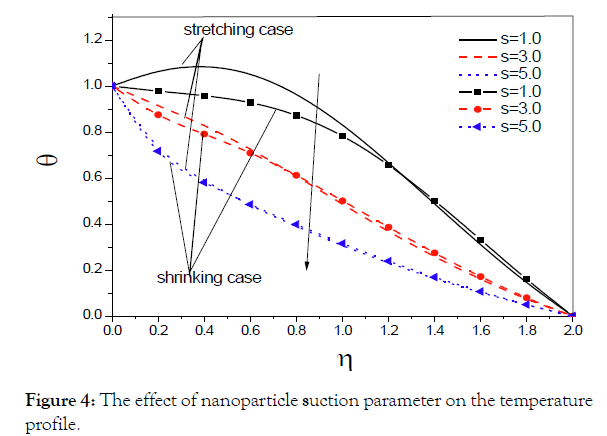
Figure 4: The effect of nanoparticle suction parameter on the temperature
profile.
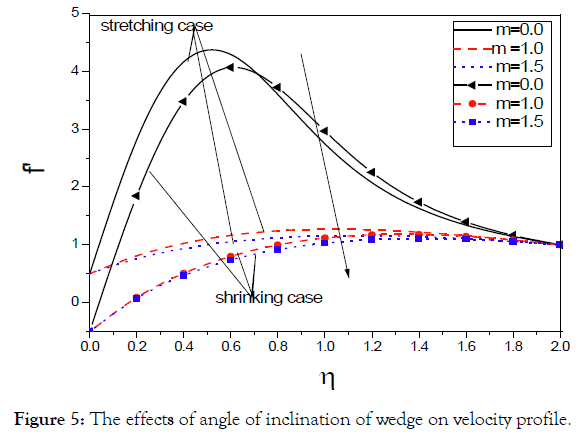
Figure 5: The effects of angle of inclination of wedge on velocity profile.
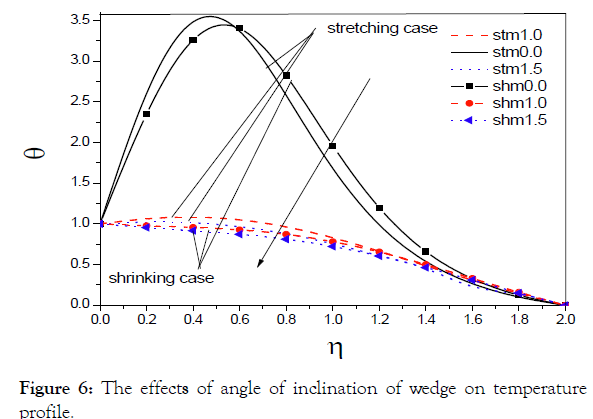
Figure 6: The effects of angle of inclination of wedge on temperature profile.
Conclusion
In this work we presented a boundary layer analysis to study the effects of nanoparticles on the behavior of fluid flow over shrinking and stretching wedge in non-Darcy medium. This research is expected to be useful for studying the movement of oil, gas, and water through the oil reservoir or the gas field, in the migration of groundwater and in the purification and purification of water. The friction factor decreases as the nanoparticle concentration increases whereas the heat transfer rate (Nusselt number) increases with nanoparticle concentration. The friction factor and heat transfer rate increase as the suction parameter increases. The friction factor decreases as the wedge angle increases whereas the heat transfer rate (Nusselt number) increases with wedge angle.
REFERENCES
- Bachok N, Ishak A, Pop I. Boundary layer stagnation-point flow toward a stretching/shrinking sheet in a nanofluid. J Heat Transfer. 2013;135(5): 054501.
- El-Dawy HA, Gorla RSR. Unsteady Flow of a Nanofluid Over a Shrinking/Stretching Porous Wedge Sheet in the Presence of Solar Radiation. J Nanofluids. 2018;7(6):1208-1216.
- Kandasamy R, Muhaimina I, Hashim B, Ruhaila A. Thermophoresis and chemical reaction effects on non-Darcy mixed convective heat and mass transfer past a porous wedge with variable viscosity in the presence of suction or injection. Nuclear Engineering and Design. 2008;238(10):2699-2705.
- Sui J, Zhao P, Cheng Z, Doi M. Influence of particulate thermophoresis on convection heat and mass transfer in a slip flow of a viscoelasticitybased micropolar fluid. Int J Heat Mass Transfer. 2018;119(1):40-51.
- Ishaka A, Nazara R, Pop I. MHD boundary-layer flow of a micropolar fluid past a wedge with constant wall heat Communications. Communications in Nonlinear Science and Numerical Simulation. 2009;14(1):109-118.
- Rosca NC, Roşca AV, Grosan T, Pop I. Mixed convection boundary layer flow past a vertical flat plate embedded in a non-Darcy porous medium saturated by a nanofluid. J Nanofluids. 2014;14(5):330-342.
- Yih KA. MHD forced convection flow adjacent to a non-isothermal wedge. Int Common Heat Mass Transfer 1999;26(6):819-827.
- Abu-Nada E, Oztop HF. Effect of inclination angle on natural convection in enclosures filled with Cu-water nanofluid. Int J Heat Fluid Flow. 2009;30(6):669-678.
Citation: El-dawy HSAE, Gorla RSR (2021) Effects of Nanoparticles on Non-Darcy Mixed Convective Heat Transfer in Nanofluids over a Shrinking and Stretching Wedge. J Nanomed Nanotech. 12: 559.
Copyright: © 2021 El-dawy HSAE, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.