Indexed In
- Open J Gate
- Genamics JournalSeek
- Ulrich's Periodicals Directory
- RefSeek
- Directory of Research Journal Indexing (DRJI)
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Proquest Summons
- Scholarsteer
- Publons
- Geneva Foundation for Medical Education and Research
- Euro Pub
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Research Article - (2019) Volume 9, Issue 2
Diffusion Control Factors Influenced the Ion Exchange between Sodium Counter Ions of Alginate and some Trivalent Metal Cations in the Sol-Gel Transition Process
Refat M Hassan*Received: 30-Apr-2019 Published: 24-May-2019
Abstract
The influence of diffusion controls on the rate of gel growth forming coordination biopolymer ionotropic spherical hydrogels resulting from ion exchange process of Na+ counter ions in alginate macromolecular chains by trivalent metal ions such as lanthanum (III)- and cerium (III) electrolyte solutions have been studied. The experimental observations indicated that the ion exchange processes in such sol-gel transformation were inherently stoichiometric processes. The influence of the nature of metal ion concentration of both alginate sol and metal ion electrolytes and temperature as well as the coordination geometry of the complexes formed have been examined. A mathematical approach of such factors which affect the gelation processes such as the mass, density and the radius of droplets of both alginate sol and formed metal-alginate hydrogels has been suggested. A tentative gelation mechanism consistent with the experimental results has been discussed.
Keywords
Coordination biopolymer; Ion exchange; Biomaterial hydrogels; Diffusion; Alginate
Introduction
In recent years, the hydrogel biomaterials were attracted a great attention owing to its wide and potential applications in biomedicine and tissue engineering such as blood anticoagulant, repairing wound dressing (nerves, cartilage, bones), kidney, adsorbent diapers, medical adhesive, binder in toothpaste, breast implant, surgical catheter as well as in sensors, biocatalysts in immobilization systems ,industrial textile and inhibitors of metal corrosion [1-3]. These polymeric biomaterials cover the targeted drug delivery to the gastrointestinal tract [2,3]. Alginate is a water-soluble anionic polyelectrolyte consists of D-mannuronic and L-guluronic acid units linked in β (1→4) position in a linear copolymer structure, bisorbent bones, medical adhesive, binder in toothpaste [4]. The monomers are arranged in a clockwise fashion around the macromolecular chains. Alginate shows a high affinity for chelation with polyvalent metal ions forming its corresponding coordination biopolymer complexes as well as inhibitors for metal corrosion [5-7] and protein crystallization screening [8,9]. The exchange process between the sodium counter ions, Na+, of alginate sol macromolecule and the polyvalent metal cations of the electrolyte solutions leads to the so-called sol-gel transformation or gelation process. These ionotropic hydrogels can be obtained in different shapes such as spheres (pellets), membranes (discs) or columns with various morphological structures depending on the apparatus used and the direction of diffusion of the inter diffused metal ions into the alginate sol for replacing the Na+ counter ions [10-12].
The effects of diffusion control on the sol-gel transformation processes for some divalent-metal alginate hydrogel complexes have been investigated earlier [13,14]. However, a lack of information still remains with respect to the diffusion controls with respect to that of the gelation processes between alginate sol and trivalent metal ions. Therefore, the role of diffusion controls in such a growth process remains unclear, not yet complete and poor understanding. This fact encouraged us to present the cited work with the aims of shedding further light on the influence of such diffusion controls on the sol-gel transformation process for trivalent-metal alginate coordinated biopolymer hydrogels in an attempt to compensate such recognized lack of information of the role of diffusion controls. Some mathematical approaches based on the physicochemical properties and geometrical configuration in those formed ionotropic hydrogel complexes were suggested for supporting the cited interpretations and discussion [15,16].
Materials and Methods
All materials used were of Analar (BDH) grade. Doubly distilled deionized water was used in all preparations. Sodium alginate used was Cica reagent (Canto Chem. Co.). Sodium alginate sols were prepared as described elsewhere by dissolving the requisite amounts of the alginate powder whilst stirring the solution vigorously and continuously to avoid the formation of lumps, which swell with difficulty [17-22]. The solutions were left aside to rest for 24 h to remove the air bubbles generated during mixing. The degree of substitution was found to be 4.34 mmolg-1 (0.95 mol-1). The measured viscosities using an Ubbelhode viscometer for were found to be 2.78 and 9.87 dl g-1 for the inherent and reduced viscosities, respectively, for 4% alginate sol in the water at 20°C.
The preparation and standardization of trivalent metal ion electrolyte solutions of different concentrations were performed as described elsewhere [23-26]. The temperature was controlled within ± 0.1°C.
Relaxation time measurements
A droplet of sodium alginate sol of known concentration was allowed to fall from a glass- syringe into a calibrated cylindrical tube of 2 cm width and 25 cm in length, containing the tested metal ion electrolyte solution of known concentration which was previously thermostated in a constant temperature air-path thermostat within ± 0.1°C. The time interval (Δτ) between the dropping and the moment at which the droplet starts to sink into the metal ion electrolyte solutions is recorded. This time interval denotes the relaxation time for gelation process between the alginate sol and the tested trivalent metal ion.
For each alginate sol and metal ion electrolyte, the same syringe was used as well as the distance from the tip of the syringe to the surface of electrolyte was kept fixed in order to maintain a nearly constant sol droplet size.
Surface Active Agents (SAA) were excluded in the cleaning of all lab-ware glasses, in order to avoid any complexity resulting from the effects of such SAA.
Acceleration of velocity measurements (dV/dt)
The time (t) for constant distances (Y) covered by the droplet while sinking into the electrolyte solution under the influence of the gravitational acceleration was recorded. The Y-t relations were plotted. From the obtained curves and by using the known graphical methods, the V-t (V=dY/dt) and (dV/dt)-V relations can be simply evaluated (where V is the velocity of the sinking of the droplet).
Unfortunately, the experimental runs using Al (III), Fe (III) and Cr (III) as trivalent metal ions in the droplet forms could not be controlled since the droplets obtained during the sol-gel transformation showed some flatness of the formed hydrogels, as well as the gels, were brittle in nature [27-34].
All experiments were prepared with different concentrations of the alginates sols and the metal ion electrolytes at various temperatures. The results used were an average of at least five experimental runs.
Results and Discussion
It was reported that the change of the droplet density dρ/dt can be taken as a measure of the rate constant of the gel-growth [23-34]. Therefore, the value (ρ1-ρ2)/ Δτ can be considered as a measure of this rate. Thus,
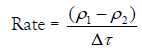 (1)
(1)
Where ρ1 denotes the density of electrolyte, ρ2 is the density of the alginate sol, and Δτ is the relaxation time.
When an alginate sol droplet comes in contact with a solution of metal ion electrolyte, a thin primary gel membrane is immediately formed around the surface of sol droplet [18,19]. This primary membrane will separate the sol droplet from the surrounding electrolyte which in turn prevents the alginate sol from dispersion outside. Since the density of droplet is smaller than that of the metal ion electrolyte, the droplet floats just below the surface of the electrolyte solution. A certain period of time is required for rearrangement of the internal structure of alginate macromolecular chains to a state nearly corresponds to the gel formation.
The macromolecular chains start to distribute themselves statically downward along the already formed membrane. When a steady state is established the sodium counter ions resulting from the dissociation of alginate sol start to migrate outward into the electrolyte solution. Simultaneously, a stoichiometric equivalent amount of the metal ions must go inward to occupy the places left by the sodium counter ions even though the counter ion mobilities and valencies of the two exchangeable ions are quite different [28,29]. The exchange process will finally lead to the sol-gel transformation phenomenon which takes place stoichiometrically as follows [30,31].
3 (Na-Alg)n + nM3+ = (M-Alg3)n + 3 (Na+ )n (2)
sol electrolyte gel electrolyte
Where Na-Alg is the sodium alginate substrate, M-Alg3 is the formed coordination biopolymer hydrogel and M is the metal ion.
As the exchange process proceeded, the density of the sol droplet is gradually increased. The increment in density is mainly due to the metal ion diffusion inside the sol droplet rather than the diffusion of the Na+ counter ions out toward the electrolyte solution. Therefore, Equation (1) may be simplified to the following relationship
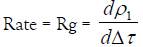 (3)
(3)
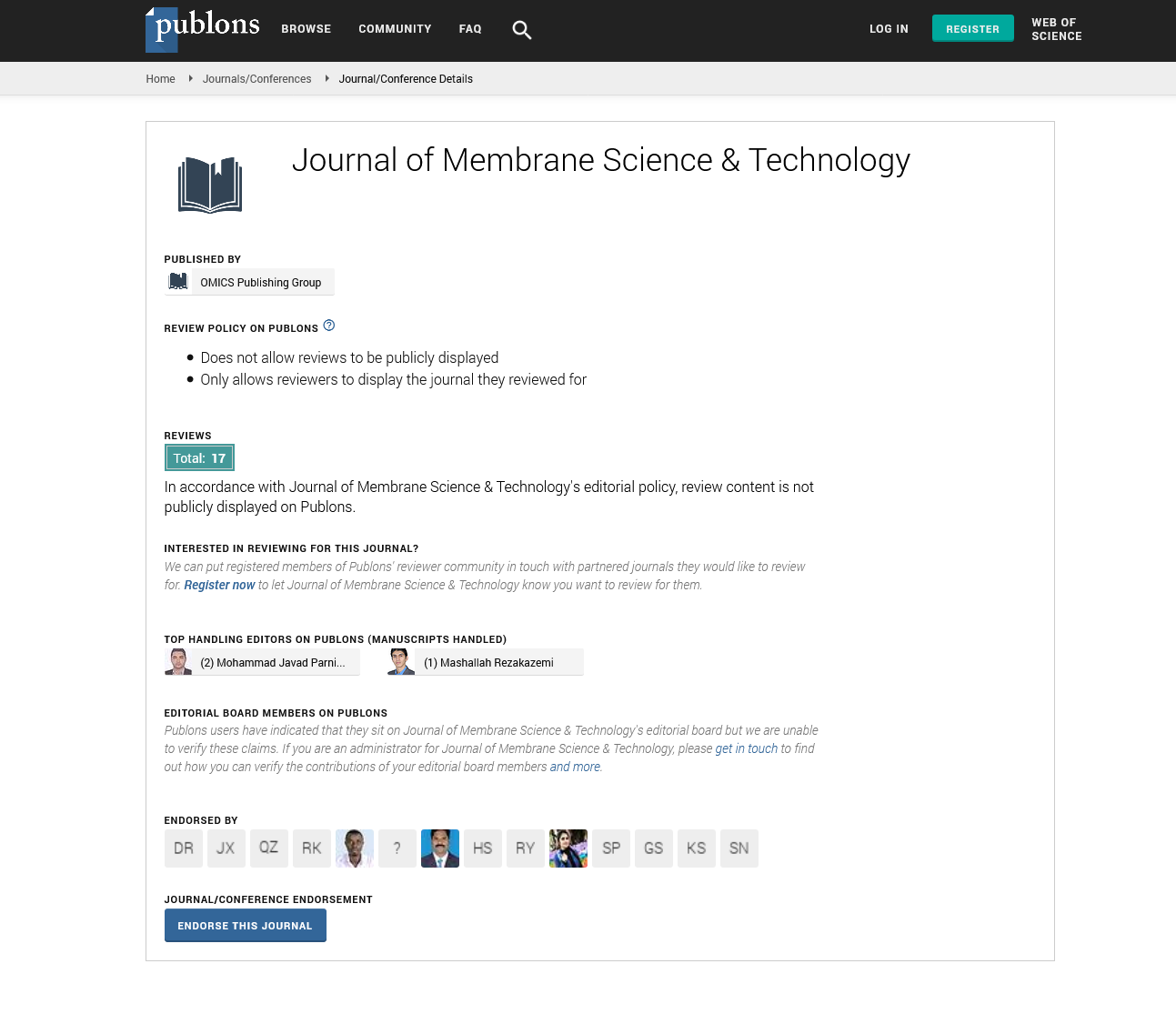
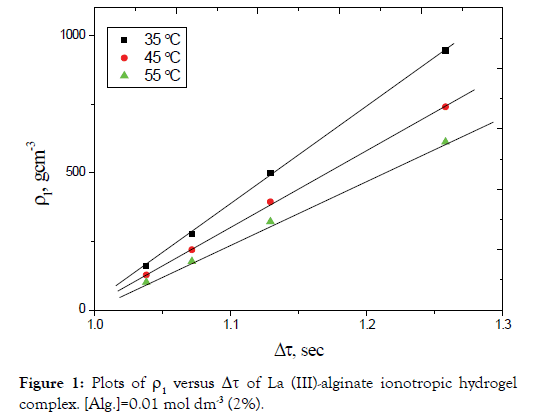
By plotting ρ1 versus Δτ for different electrolyte concentrations, straight lines were obtained as shown in Figures 1 and 2. The slopes of these lines are taken as a measure of the rate constants of gel growth (Rg). The values of Rg were calculated by the leastsquares method and are summarized in Table 1.
| Dt, sec | La(III) | Ce(III) | ||||
|---|---|---|---|---|---|---|
| 35°C | 45°C | 55°C | 35°C | 45°C | 55°C | |
| 945 | 740 | 612 | 919 | 745 | 625 | |
| 104 Rg, g cm-3s-1 | 2.8 | 3.95 | 4.18 | 2.58 | 3.17 | 3.76 |
Table 1: The relaxation time (ï„ï´) and rate of gel growth of some trivalent metal alginate hydrogel complexes. [Alg.]=0.01 mol dm-3 (2%).
Figure 1. Plots of ρ1 versus Δτ of La (III)-alginate ionotropic hydrogel complex. [Alg.]=0.01 mol dm-3 (2%).
Figure 2. Plots of ρ1 versus Δτ of Ce (III)-alginate ionotropic hydrogel complex. [Alg.]=0.01 mol dm-3 (2%).
The magnitude of the rate constants of gel-growth obtained in the present study was found to be in good agreement with that determined kinetically [34]. This result may confirm the validity of the suggested rate-law expression defined by Equation (3).
The rate of formation of the primary membrane was found to affect the rate constant of the gel-growth depending on the concentration of both alginate sol and the metal ion electrolyte. Such a rate is high in metal ion electrolyte solutions of lower concentrations rather than in higher ones due to the high mobility of metal ions in the former case. On the contrary, these rates are high in sols of higher concentrations rather than in lower ones owing to the presence of many exchange sites within the alginate macromolecular chains in the former sols in comparison to that in the latter ones [23,24] (Figures 2 and 3).
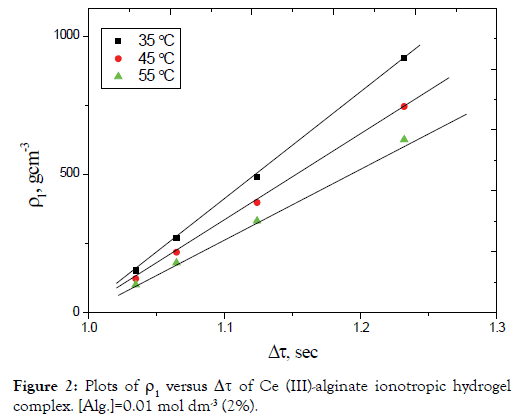
Figure 3. The acceleration-velocity relationship for a falling droplet (case I, II and III).
The pH of the electrolyte solution is known to affect the width of capillaries formed in these ionotropic gels. Increasing the pH of the electrolyte will increase the capillary width and, hence, increases the rate of exchange between the exchanging counter ions [10-13,23,24]. The net result is a decrease in the relaxation time period.
The formed coordination biopolymer metal-alginates of colloidal hydrogel forms were characterized with elastic modulus, clarity and fine network structure [34,32-39]. The geometrical configuration of these formed metal-complexes hydrogels may be represented by Scheme I [34,40]. These gels are ionotropic in nature as a result of the orientation of both the solvent molecules and the macromolecular chains of the alginate toward the interdiffused metal ions.
The kinetic parameters of gelation were calculated from the temperature dependence of the rate of gel-growth. Plots of ln Rg versus 1/T of Arrhenius equation gave good straight lines from whose slopes, the activation energies were obtained (E≠). Again, plots of 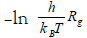 against 1/T of Eyring equation were found to be linear from whose slopes and intercepts the enthalpies and entropies of activation were obtained. These kinetic parameters were calculated using the least- squares method and are summarized in Table 2. The magnitude of Ea≠ may reflect the stability of these metal alginate ionotropic gel complexes. The values of activation energies observed in Table 3 indicated that the stability decreases in the order Ce(III)- ≥ La(III)-alginate complex in good agreement with that stated previously [34,41]. Moreover, the large negative values for the entropy of activations observed are not surprising. This may be attributed to the necessity of the small metal ions used to penetrate the spaces between the large carboxylate groups in order to bring them together through an egg-carton like structure via sort of bridge formation [13,40-45].
against 1/T of Eyring equation were found to be linear from whose slopes and intercepts the enthalpies and entropies of activation were obtained. These kinetic parameters were calculated using the least- squares method and are summarized in Table 2. The magnitude of Ea≠ may reflect the stability of these metal alginate ionotropic gel complexes. The values of activation energies observed in Table 3 indicated that the stability decreases in the order Ce(III)- ≥ La(III)-alginate complex in good agreement with that stated previously [34,41]. Moreover, the large negative values for the entropy of activations observed are not surprising. This may be attributed to the necessity of the small metal ions used to penetrate the spaces between the large carboxylate groups in order to bring them together through an egg-carton like structure via sort of bridge formation [13,40-45].
| V | La(III) | Ce(III) |
|---|---|---|
| 0.32 | 0.31 | |
| 2gr2 (ρ2'-ρ1)/9h | 0.47 | 0.42 |
Table 2: The values of V at 2gr2(ρ2'-ρ1)/9η of some trivalent metal alginate hydrogel complexes. [Alg.]=0.01 mol dm-3 (2%).
| Weight of droplet, g | La(III) | Ce(III) |
|---|---|---|
| 2.82 × 10-2 | 2.81 × 10-2 | |
| Volume of droplet, cm-3 | 2.50 × 10-2 | 2.50 × 10-2 |
| Density, g cm-3 | 1.13 | 1.12 |
| Radius, cm | 0.17 | 0.16 |
| % of water content | >97 | >97 |
Table 3: Some physical properties of some trivalent metal alginate hydrogel complexes. [Alg.]=0.01 mol dm-3 (2%).
After the relaxation time interval has elapsed, i.e. the density of the droplet exceeds that of the surrounding electrolyte, the droplet starts to sink into the electrolyte solution with an appreciable velocity (V).
In sol-gel transformation processes, the structural peculiarities and the hindrance results from the relative movements of the particles owing to the various interchain linkages may cause some shifts to take place very slowly [42]. Hence, the time necessary for the droplet to have surface properties distinctly different from those of the sol and its density will exceed that of the surrounding electrolyte may be termed as the relaxation time.
The nature of the metal ions; radius, volume and density of the droplet; concentration and pH of the electrolyte as well as the concentration and viscosity of the alginate sol were found to play an important role in the magnitude of Δτ [14-16,34]. Each metal alginate complex has a characteristic Δτ value. This value was found to decrease with increasing the concentration of alginate sol, whereas it increased with increasing the metal ion concentration. Again, the change of Δτ with changing the radius of metal ion (r') can be explained by the change in mass, size and radius (r) of the gel droplet depending on the tendency of the gel droplet for swelling or shrinking in aqueous solutions [14-16]. Since the physical properties such as the mass, density and ionic radius of both Ce (III) and La (III) are nearly equal [24], the relaxation time in these two hydrogel complexes is expected to be the same as was experimentally observed (Table 3). In addition, the values of Δτ were found to decrease with increasing temperature as shown in Table 1.
Moreover, the relaxation time can also be explained by the remarkable dependence of the velocity of acceleration upon the alginate sol concentrations which increase with increasing the concentration of the sol and vice versa.
It is believed that the densities of both the sol droplet and electrolyte are the only determining factors for the magnitude of the velocity of acceleration of sinking for the droplet into the electrolyte solution after the relaxation time has been elapsed [22]. The radius, mass, and gravitational forces play a role in such a sinking (Table 3). Therefore, a mathematical treatment involving all these factors has been developed. Let us, suggested that there are three forces acting on such spherically shaped alginate sol droplet. The first one being the weight of the droplet (F1↓)
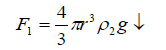 (4)
(4)
Where r is the radius of the droplet that depends on the radius of the metal ion (r') and g is the gravitational force. The second force is the Archimedean force (F2↑), thus,
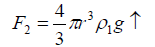 (5)
(5)
The third one is the dragging force (F3↑) which depends on the velocity of the falling droplet, i.e.,
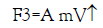 (6)
(6)
where m is the mass of the droplet and A is the proportional constant which depends on the viscosity of the medium and the radius of the falling droplet,
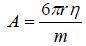 (7)
(7)
Where η denotes the viscosity of the electrolyte solution.
As the sol droplet gets in contact with the metal electrolyte solution, the droplet velocity is equal to zero and, hence, the dragging force (F3) can be omitted, i.e.,
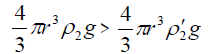 (8)
(8)
Therefore, the droplet floats just below the surface of electrolyte at the beginning.
When the density of the droplet (ρ2') exceeds that of the surrounding metal ion electrolyte as a result of the exchanging process between the two different metal counterions (i.e. >Δτ), the droplets start to sink into the electrolyte solution with an appreciable velocity. The behavior of sinking is controlled by the conditions
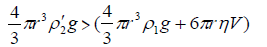 (9)
(9)
Equation (9) requires that the velocity of the droplet (V) should be less than the factor 2gr2 (ρ'2-ρ1)/9η, as is experimentally observed (Table 4).
| E≠a, KJ mol-1 | La(III) | Ce(III) |
|---|---|---|
| 17.95 (17.65) | 15.91 | |
| A, mol s-1 | 0.31 (-) | 0.13 |
| ΔH≠, KJ mol-1 | 15.31 (9.98) | 13.28 |
| ΔS≠, J mol-1 K-1 | -263.41 (-282.64) | -270.73 |
| Δ G≠, KJ J mol-1 | 93.80 (94.21) | 93.96 |
Table 4: The values of the activation parameters of some trivalent-metal alginate hydrogel complexes. [Alg.]=0.01 mol dm-3 (2%). The values between brackets were obtained kinetically [24].
In order to account for the effect of the diffusion controls on the acceleration of velocity, the following equation of motion is suggested
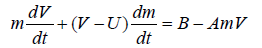 (10)
(10)
where U is the velocity of the reduced mass just after leaving the droplet to the electrolyte surface and B is constantly equal to [ g (2-ρ1)]/ ρ2.
Assuming that the reduced mass becomes immediately at rest after droplet leaving (U=0), hence Eq. (10) reduces to
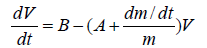 (11)
(11)
The analysis of Eq. (11) can be completely understood if we considered the following assumptions:
Case I
Assuming that both the mass and density of the droplet are constants during the gelation process (dm/dt=0), Eq. (11) leads to
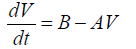 (12)
(12)
Where V=A/B(1-e-Bt) .
Equation (12) requires that the plots of dV/dt against V should be linear with a slope to (-A) and intercept on dV/dt axis equal to (B). This straight line may be represented by (a-b) line on the theoretical curve shown in Figure 3.
Case II
Assuming that the mass of the droplet remains constant while its density is subjected to change as a result of cross-linking results from the inter diffused metal ions as well as the orientation of the macromolecules and solvent molecules toward the chelated metal ion, then Equation (11) leads to Equation (12), with variables A and B. The term B increases by increasing ρ2` due to the decrease in r, while the term A is consequently decreased. The values of dV/ dt are increased when compared with that obtained in Case I.
On the other hand, if the droplet radius decreases with a continuous increase in its density, a behavior similar to that illustrated by the line (II) in Figure 3 is obtained. Moreover, if the decrease in the radius of the droplet occurs in a rhythmic manner, i.e. in a pulsed way then we will obtain the line (III), which coincides with the line (I) for the same interval time.
Case III
If the mass of the droplet decreases while its radius remains constant owing to the outward flux of water (dehydration), then the B term increases while the A term is decreased. Therefore, the term B–AV yields a decrease in dV/dt in Eq.(11). At the same time, the term dm/dt will increase in magnitude and possesses a negative sign.
The resultant of dV/dt will depend on whether or not the rate of (A-BV) decrease is greater than the rate of dm/dt increase. If dV/ dt<6ηr, then 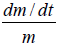 may even assume to be a negative value.
may even assume to be a negative value.
The acceleration of velocity can be determined from Y-t plots. Then the term dV/dt can be evaluated using the well-known graphical methods [32,35]. The results are summarized in Table 5.
| La (III) | Ce(III) | ||
|---|---|---|---|
| 102 V cm s-1 | 103 (dV/dt) | 102 V cm s-1 | 103 (dV/dt) |
| 0.27 | 4.4 | 0.27 | 2.6 |
| 0.4 | 6.6 | 0.4 | 3.15 |
| 0.53 | 6.55 | 0.52 | 3.25 |
| 0.66 | 13.2 | 0.65 | 6.4 |
| 0.79 | 6.45 | 0.78 | 4.23 |
| 0.92 | 6.5 | 0.91 | 6.3 |
| 1.05 | 6.4 | 1.03 | 6.3 |
| 1.18 | 6.35 | 1.16 | 6.3 |
Table 5: The values of V and dV/Dt of some trivalent metal alginate hydrogel complexes. [Alg]=0.01 mol dm-3 at 45°C.
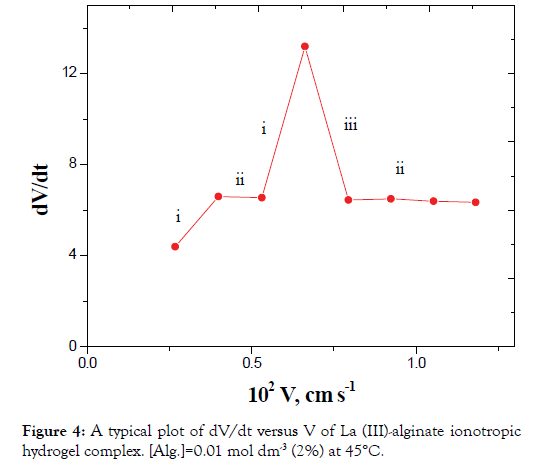
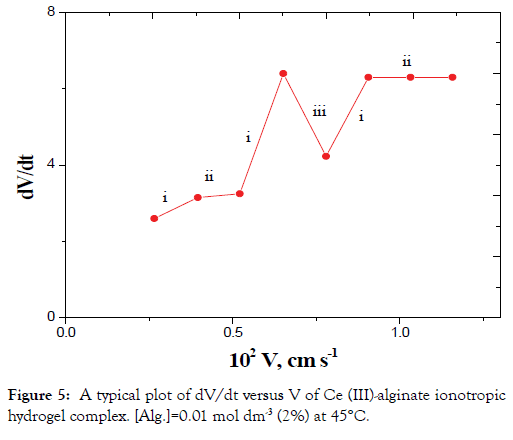
The plots of dV/dt versus V gave pulsed behavior as shown in Figures 4 and 5. The parts of (i) on the curves represent the sudden increase in acceleration of the velocity of the falling droplet due to a decrease in r with a corresponding increase in ρ2 without considerable change in m (Case II). This behavior can be attributed to the orientation of the solvent molecules and macromolecular chains toward the metal ions resulting from cross-linking.
Figure 4. A typical plot of dV/dt versus V of La (III)-alginate ionotropic hydrogel complex. [Alg.]=0.01 mol dm-3 (2%) at 45°C.
Figure 5. A typical plot of dV/dt versus V of Ce (III)-alginate ionotropic hydrogel complex. [Alg.]=0.01 mol dm-3 (2%) at 45°C.
The parts (ii) on the curves correspond to a simultaneous effect of the radius contraction, mass decrease and falling according to Stokes law (case I).
The parts (iii) on the curves represent the sudden decrease in acceleration of the velocity of the droplets. These parts represent the decrease in mass as discussed in case III with almost constant r and decrease of the ρ2 values.
In view of these interpretations and the experimental results, the gel growth is a rhythmic process in nature and this agreed very well with the behavior for other metal alginate gel complexes observed previously (Figures 3-6) [46-47].
Figure 6. Intermolecular Association; Scheme I: Chelation in trivalent metal ion-alginate hydrogel complexes.
Conclusion
When a sodium alginate sol is dropped into an electrolyte solution of polyvalent metal ion, a primary membrane is simultaneously formed around the droplet to give it a symmetrical spherical shape. The droplet will float just below the surface of electrolyte for a certain period of time (Δτ) for replacing the sodium counter ions of the alginate macromolecule by the polyvalent metal ion. This exchange process is called the sol-gel transformation. After a certain period of time (>Δτ), the droplet starts to sink into the electrolyte solution with appreciable velocity. Several factors were found to affect the rate of gel-growth in these droplets such as the relaxation time and velocity of acceleration under the influence of gravitational force. The experimental results reveal that the stability of the metal alginate complexes studied increases in the order La (III)<Ce (III)-alginates. A mathematical approach for examining the affecting factors have been presented and discussed.
Acknowledgment
The author would like to present his grateful acknowledgment with thanks to the Editor for his appreciated concern. Thanks are also due to Chemistry Department, Research Center for Materials Science, Nagoya University and Chemistry Department, Faculty of Applied Sciences, Umm Al-Qura University, Makkah Al- Mukarramah, the Saudi Arabia Kingdom for their continued cooperation and support of the scientific research.
REFERENCES
- Calo E, Khutoyanskly VV. Biomedical applications of hydrogels: A review of patent and commercial products. Eur Poly J. 2015;65:252-267.
- Muzzarelii AA. Chitin and chitosan for the repair of wounded skin, nerve, cartilage and bone. Carbohyd Poly. 2009;76:167-182.
- Giovagnoli S, Givanni L, Blasi P, Mancuso F, Schoubben A, Arato I, et al. Alginates in pharmaceutics and biomedicine: Is the future so bright. Curr Pharmac Design 21. 2015:4917-4935.
- Saha N, Saarai A, Ray N, Kilano T, Shasha P. Polymeric biomaterial based hydrogels for biomedical application. J Nanotech. 2011;2:85-90.
- Hassan RM, Zaafarany IA. Kinetics of corrosion inhibition of aluminum in acidic media by water-soluble natural polymeric pectates as anionic polyelectrolyte inhibitors. Materials. 2013;6:2436-2451.
- Lin Y. What’s happened over the last five years with high throughput protein crystallization screening? Expert Opin Drug Discov. 2018;13:691-695.
- Grey JL. Challenges and opportunities for few protein crystallization strategic in structure based drug design. Expert Opin Drug Discov. 2010;5:1039-1045.
- Lin Y, Bogdanov M, Lu S, Guan Z, Margolin W, Weiss JP, et al. The phospholipid repair system LpII/Aas in Gram-negative bacterial membrane envelope from host phospholipase A2 attack. J Biol Chem 2018;293:3386-3398.
- Hasanin MDS, Nayok AK (Eds). Alginate-based composite in drug delivery applications, in "Alginates verstile polymer in biomedical applications and therapeutics. Taylor and Francis Publishing Group. 2019:1-23.
- Whistler RL, Kirby KW. Compounds and behavior of polysaccharides. Z Physiol Chem. 1955;314:46.
- Fischer FG, Dorfel H. The polyuronic acids in brown algae. Z Physiol Chem. 1955;302:186-203.
- Rees DA. Polysaccharides gels: A molecular view. Chem Ind. 1972:630-636.
- Rees DA, Samuel JWB. The structure of alginic acid: Part VI. Minor feature and structural variation. J Chem Soc. 1967:2295-2298.
- Schweiger R. Acetyl pectates and their reactivity with polyvalent metal ions. J Org Chem. 1964;29:2973-2975.
- Smidsrod O. Molecular basis for some physical properties of alginates in the gel state. Faraday Discuss. 1964;57:263-274.
- Smidsrod O, Skjak-Brack G. Alginate as immobilization matrix for cells. Trends Biotechnol. 1990;8:71-78.
- Hassan RM, Wahdan MH, Hassan A. Kinetics and mechanism of sol-gel transformation on polyelectrolytes of nickel alginate ionotropic membranes. Eur Polym J. 1988;24:281-283.
- Hassan RM, El-Shatoury SA, Mousa MA. Kinetics and mechanism of sol-gel transformation on polyelectrolytes of capillary copper alginate ionotropic membranes. Eur Polym J. 1988;24:1173-1175.
- Hassan RM, Gobouri A, Zaafarany IA. Kinetics and mechanism of sol-gel transformation between sodium alginate anionic polyelectrolyte and some alkaline earth metal ions with formation of coordination biopolymer ionotropic polymembrane hydrogels of capillary structures. Advan Biosen Bioelect. 2013;2:47-56.
- Hassan RM, Makhlouf MTh, Summan AM, Awad A. Influence of frequency on specific conductance of polyelectrolyte gels with special correlation between strength of chelation and stability of divalent metal alginate ionotropic gels. Eur Polym J. 1989;25:993-996.
- Thiele H, Indreson G. Ionotropic gels of polyuronic acids. Part II. Degree of order. Koll Z. 1955;176:140-145.
- Thiele H, Hallich KH. Capillary structure in ionotropic gels. Koll Z. 1957;151:1-12.
- Thiele H. Ionotropic gels of polyuronic gels. Part III. Degree of order. Koll Z. 1962;182:24-30.
- Hassan RM, Makhlouf MTh, El-Shatoury SA. Alginate polyelectrolyte ionotropic gels. Part IX: Diffusion controls effects on the relaxation time of sol-gel transformation for transition divalent metal alginate ionotropic gel complexes. Coll Poly Sci. 1992;270:1237-1242.
- Khairou KS, Al-Gethami WM, Hassan RM. Diffusion controlled relaxation time and acceleration of velocity of sol-gel transformation of cross-linked metal alginate ionotropic gel complexes. Bull Polish Acad Sci Chem. 2003;51:207-220.
- Karagunduz A, Unal D. New method for evaluation of heavy metal binding to alginate beads using pH and conductivity data. Adsorption.2006;12:175-184.
- Vogel AI. Text book of quantitative inorganic analysis, 4th ed., Longmans, London. 1978;198.
- Hassan RM, Zaafarany IA, Gobouri AA, Tirkistani FA, Fawzy A, Takagi HD. Polymeric biomaterial hydrogels. II. Behavior of some coordination biopolymeric metal alginate ionotropic hydrogels in aqueous solutions. J Life Medicine. 2013;41-47.
- Awad A, El-Cheikh F, Shaker A. The diffusion control in sol-gel transformation. Coll Poly Sci. 1980;258:1244-1249.
- Awad A, El-Cheikh F, Shaker A. The diffusion control in sol-gel transformation. J Ind Chem Soc LV II. 1980;728-731.
- Haugh A, Smidsrod O. The effect of divalent metals on the properties of alginate solutions II. Comparison of different metal ions. Acta Chem Scand. 1965;19:341-351.
- Hellferich FG. Ion Exchange. McGraw-Hill, New York. 1962.
- Hassan RM. Influence of frequency on electrical properties of acid and trivalent metal alginate ionotropic gels. A correlation between strength of chelation and stability of polyelectrolyte gels. High Perf Poly. 1989;1:275-284.
- Hassan RM, Summan AM, Hassan MK, El-Shatoury SA. Kinetics and mechanism of sol-gel transformation on polyelectrolytes some transition metal ions especially cobalt alginate ionotropic membranes.Eur Poly J. 1989;25:1209-1212.
- Zaafarany IA. Kinetics of sol-gel transformation between some trivalent-and tetravalent-metal ions and sodium alginate anionic polyelectrolyte with formation of coordination biopolymeric structure polymembranes hydrogels of capillary structures. J Advancs Chem. 2013;3:133-142.
- Hassan RM, Awad A, Hassan A. Seperation of metal alginate gels to polymembranes with special evidence on the position of chelation in copper alginate complex. J Poly Sci Part A. 1991;29:1645-1648.
- Thiele H, Hallich K. Capillary Structure in Ionotropic Gels. Koll Z. 1957;151:1-12.
- Thiele H. Structure Formation by Ion Diffuse. Simplex Ionotropism. Z Naturforch. 1957;12:14B-23B.
- Thiele H, Anderson G. Ionotropic gels of polyuronic gels. Part III. Degree of order. Koll Z. 1962;76:140-145.
- Thiele H. Ordered coagulation and gel formation. Discuss Farad Soc. 1954;18:294-301.
- Hassan RM. Alginate polyelectrolyte ionotropic gels. XIII. Geometrical aspects for chelation in metal alginate complexes related to their physicochemical properties. Poly Int. 1993;31:81-86.
- Tirkistani FA, Hassan RM. Kinetics and mechanism of the non-isothermal decomposition of some cross-linked metal alginate complexes especially trivalent-metal alginate complexes. Orient J Chem. 2012;28:913-920.
- Lambe H. Mechanics for engineers and scientists, Pergamon Press, London. 1950.
- Hassan RM, Tirkistani FA, Zaafarany IA, Fawzy A, Khairy M, Iqbal S. Polymeric biomaterials hydrogels I. Behavior of some ionotropic cross-linked metal alginate hydrogels especially copper-alginate membranes in some organic solvents and buffer solutions. Advancs Biosci Biotechnol. 2012;2:845-854.
- Cotton FA, Wilkinson G. Advanced Inorganic Chemistry. 3rd Edn., John Wiley and Sons, New York. 1972.
- Laidler KJ. Chemical Kinetics, 2nd Edn., Tata McGraw-Hill, New Delhi. 1983.
- Awad A, El-Cheikh F, Hassan RM. Kinetics of sol-gel transformation especially ionotropic gels. Rev Roum Chimie. 1979;24:563-569.
Citation: Hassan RM (2019) Diffusion Control Factors Influenced the Ion Exchange between Sodium Counter Ions of Alginate and some Trivalent Metal Cations in the Sol-Gel Transition Process. J Membr Sci Technol 9:198.
Copyright: © 2019 Hassan RM. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.