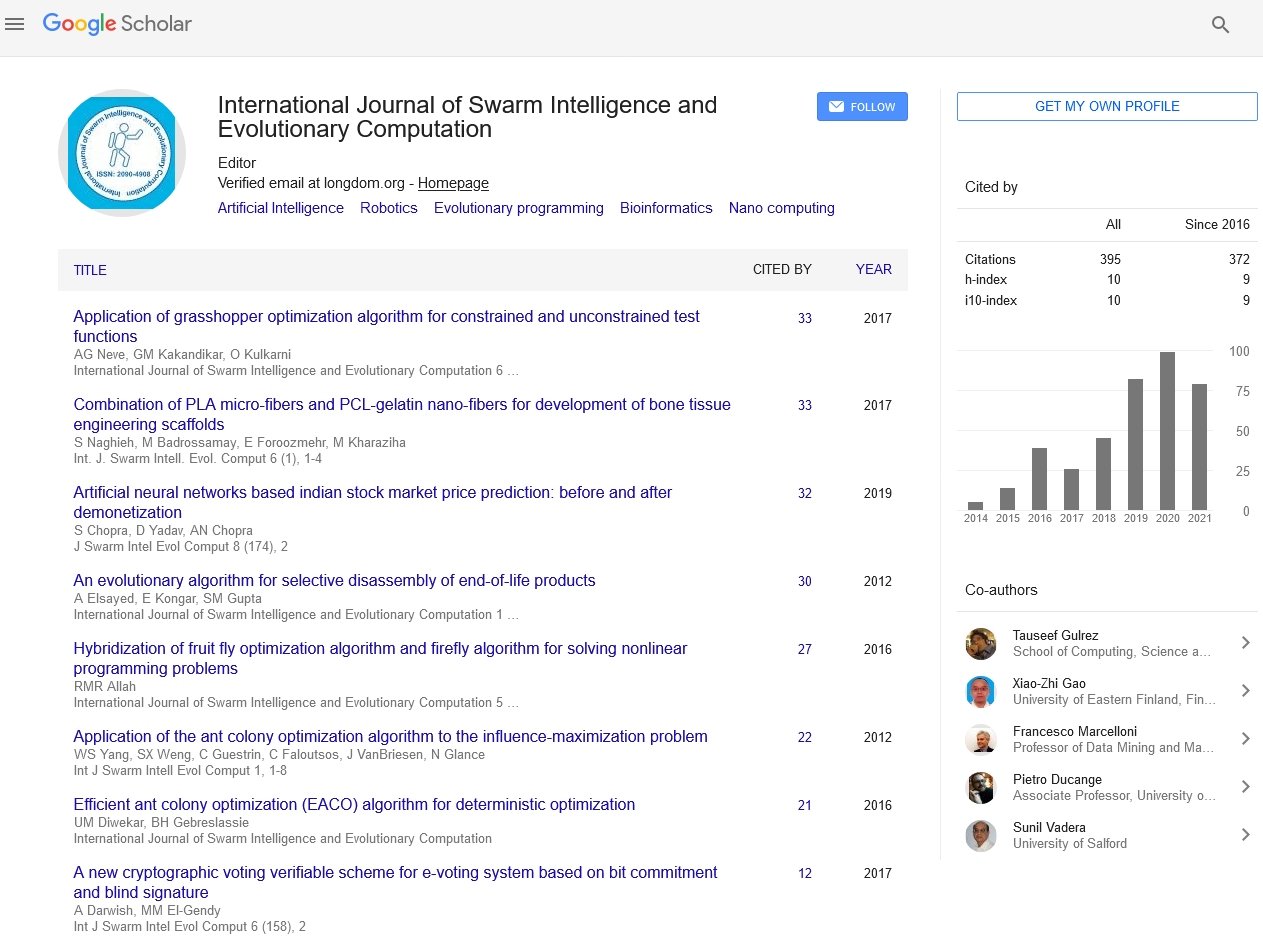
Indexed In
- Genamics JournalSeek
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Publons
- Euro Pub
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Review Article - (2022) Volume 11, Issue 7
Coupled Stochastic Chaos and Multifractal Turbulence in an Artificial Financial Market
Carlos Pedro Gonçalves*Received: 03-Jul-2022, Manuscript No. SIEC-22-17299; Editor assigned: 05-Jul-2022, Pre QC No. SIEC-22-17299(PQ); Reviewed: 22-Jul-2022, QC No. SIEC-22-17299; Revised: 02-Aug-2022, Manuscript No. SIEC-22-17299(R); Published: 12-Aug-2022, DOI: 10.35248/2090-4908.22.11.261
Abstract
A stochastic chaos model of adaptive financial speculative dynamics is introduced and shown to capture several key features of actual financial turbulence, including power law scaling in the squared logarithmic returns’ distribution, 1/f spectral signatures and multifractal scaling, the model is expanded to a multiple asset artificial financial market, leading to a coupled stochastic chaos model of financial speculative dynamics, showing evidence of macroscopic financial turbulence, with excess kurtosis, power law signatures, multifractal scaling at the mean field level as well as a relation between dynamical synchronization and financial volatility dynamics. The implications for financial theory and applications of coupled stochastic chaos models to model complex financial coevolutionary dynamics are addressed
Keywords
Stochastic chaos; Coupled nonlinear maps; Multifractal turbulence; Adaptive market hypothesis; Selforganized criticality; Co-evolutionary models
Introduction
We introduce a stochastic chaos model of adaptive financial speculative dynamics and show that it is able to capture several key features of actual financial turbulence, including power law scaling in the squared logarithmic returns’ distribution, 1/f spectral signatures in the squared logarithmic returns’ power spectrum and multifractal scaling, we show that these features are present both with and without noise coupling (that is, in the underlying deterministic chaos dynamics), but an increasing noise coupling tends to lead to an exponential rise in kurtosis and market turbulence.
The model is first addressed in a single asset framework and then expanded to a multiple asset artificial financial market, leading to a coupled stochastic chaos model of financial co-evolutionary speculative dynamics, showing evidence of macroscopic financial turbulence, with excess kurtosis both at the local asset level and at the mean field level, power law signatures, multifractal scaling both at the local asset level and at the mean field level as well as a relation between dynamical inter-asset synchronization and financial volatility dynamics. The implications for financial theory and applications of coupled stochastic chaos models to finance are also addressed.
In section 2, we provide for the background to the financial turbulence modelling problem and main references linked to the complexity paradigm underlying the research on power law signatures and multifractal scaling in finance, this section reviews the main foundations for the nonlinear adaptive market model studied in sections 3 and 4.
In section 3, we review Bachelier’s theory of speculation and revise it by introducing and studying a single asset stochastic chaos model for the financial returns’ dynamics with adaptive speculator dynamics consistent with the Adaptive Market Hypothesis (AMH), showing that it is already capable of producing the main features of financial turbulence, including power law signatures and multifractal scaling, both without the noise coupling (deterministic chaos) and with the noise coupling (stochastic chaos). In section 4, we expand the model to a multiple asset framework introducing a speculator driven artificial financial market and in section 5, we review the model’s main findings including the sources of turbulence and the main patterns associated with macroscopic inter-asset synchronization and financial volatility dynamics.
The focus on speculation allows us to work the financial theory from its foundations with few assumptions revision, showing that a speculator-driven market with adaptive dynamics, where speculative build-ups are followed by market correction, coupled with a dynamical volatility associated with the size of speculators’ impact on the financial returns is already capable of leading to turbulent financial dynamics, power law signatures and multifractal chaos, as well as a dynamical relation between inter-asset synchronization and risk.
Turbulence and Complexity in Financial Returns Dynamics
Bachelier’s theory of speculation assumed that financial speculators process a maximal diversity of information in such a way that they operate independently from each other and randomly so, compensating for each other’s moves leading to a final Gaussian structure for financial price dynamics and a random walk for price dynamics in discrete time with the Brownian motion being the continuous time limit model, this model was subsequently changed to a lognormal model of price dynamics with the assumption behind the speculative behavior holding nonetheless and the Gaussian structure assumed for the logarithmic returns leading to the Geometric Random Walk (GRW) model of price dynamics and the geometric Brownian motion as its continuous time limit [1-4].
This theory fails, however, in accounting for actual financial time series turbulence, which shows evidence of power law scaling and long memory in volatility observables such as the squared logarithmic returns of both individual assets and stock market indices, multifractal signatures and, even, evidence of some form of stochastic chaos dynamics, with chaotic signatures surfacing in different studies [5-15]. Since a financial system involves multiple assets, considering this evidence raises the plausibility of the hypothesis for the presence of stochastic networked chaos associated with financial dynamics as the underlying source for the emergent turbulence signatures as a form of chaos-induced selforganized criticality.
Indeed, power law scaling in statistical distributions of dynamical variables and in power spectra have been identified as hallmarks of a type of dynamics called Self-Organized Criticality (SOC) [16- 19]. In the financial markets, these SOC signatures are associated with logarithmic returns volatility dynamics, which ranges in a continuous scale.
While “pile of sand” models were initially proposed by Bak, Tang, and Wiesenfeld as a basic model for SOC, the possibility of SOC associated with chaotic signals, that is, signals coming from chaotic dynamics that do not generate a white noise spectrum but rather 1/f power spectra and power law decay in signals probability distributions was raised by Chang regarding magnetic turbulence in the dynamics of the Earth’s magnetotail, in this case, the SOC included also multifractal scaling. A link also between 1/f spectra and chaos in nonlinear dynamical systems was researched by Handel, who provided for a “1/f noise criterion for chaos in nonlinear systems” with consequences for turbulence modelling, strengthening the possibility of chaos as a source of SOC [20].
The existence of chaotic maps that can lead to power law signatures in chaotic signals’ densities and power spectra (1/f chaos) as well as exhibiting multifractal signatures opens up the possibility of chaos as another possible source of SOC with implications for finance with chaos being shown to lead to all the hallmarks of SOC in applications of coupled chaotic maps to financial economics as well as in applications of coupled chaotic maps to neuroscience and turbulence modelling [21].
In the present work, we introduce a multiple asset artificial financial market based on coupled nonlinear maps of noisy chaotic oscillators that is able to capture the above main features of financial turbulence including the main power law signatures and multifractal scaling that characterize the SOC signatures in finance. The model is based on a revision of Bachelier’s main assumption that speculators operate independently as uncorrelated individuals, forming beliefs on a diversity of information that leads to a probabilistic balancing of the reasons for buying and selling, instead, we build a nonlinear model for the formation of speculative trends and subsequent market corrections with a nonlinear volatility feedback, following Lo’s Adaptive Market Hypothesis (AMH), which applies Complex Adaptive Systems (CAS) science to financial markets, in this way, by revising Bachelier’s original assumption, under Lo’s AMH framework, we consider a collective nonlinear adaptive dynamics by speculators that can lead to speculative buildups driving market upwards or downwards, trends that are broken by market corrective movements, coevolving with market volatility, in a coupled multiple asset artificial financial market [22].
Microscopic financial modelling based on the construction of artificial financial markets provides for a way to study how foundational assumptions regarding investor behavior, investment strategies and financial microstructure can influence financial market dynamics, especially in an attempt to provide for a theoretical underpinning on financial market turbulence markers and key features [23-26]. This approach, which has characterized the complexity approach to economics contrasts with stochastic process approaches that provide for top-down probabilistic models of financial price dynamics, often making unrealistic assumptions in order to obtain analytical tractability.
Coupled chaos models, in turn, offer a bridge between the two approaches. These models were introduced to provide for a framework on which to study dynamics of spatially extended systems with a large number of degrees of freedom, providing for a conceptual basis on which to study networks of chaotic oscillators and pattern formation as well as being powerful conceptual tools in complex systems modelling [27-31]. Networked chaotic maps, which include, as two major models, Coupled Map Lattices (CMLs) and Globally Coupled Maps (GCMs), are advantageous in dealing with networked complex systems where the basic dynamical nodes behave as chaotic oscillators, in this context, this leads to the research field of high dimensional chaos which shows specific features that distinguish it from a basic stochastic process, including complex emergent patterns with a high effectiveness in addressing networked dynamical systems and turbulence.
From a financial standpoint, artificial financial markets comprised of networks of chaotic oscillators, such as the one we study here, provide for a basis on which to address multiple assets’ dynamics [32]. Indeed, in financial markets, one does not have a single asset framework, which means that multiple asset linkages need to be taken into account, especially in portfolio risk considerations as well as in the study of emergent macroscopic turbulent financial dynamics observed in financial indices which show that turbulence risk is not erased by portfolio construction.
Furthermore, financial evidence favors that inter-asset correlations are dynamical, rather than fixed as assumed in portfolio theory, resulting from complex synchronization patterns between different assets’ financial returns, in particular, in periods of high volatility as well as in events such as market crashes this synchronization seems to occur and reduce the effect of risk diversification from portfolio investment.
In this way, coupled chaos models provide for a way in which to approach a multi-asset financial turbulence and complex synchronization dynamics in financial markets, these models were applied in to the construction of an artificial economy with a coupled financial market where direct competitors operating in a market for goods also have their shares traded in the financial market, this economy was modelled with both deterministic coupled chaotic maps and with stochastic coupled chaotic maps with different investor types and coevolving investor dynamics, already showing evidence of multifractal turbulence in financial market dynamics and a joint macroscopically far-from-equilibrium economic dynamics, illustrating the effectiveness of coupled chaos models in multiple asset microscopic financial modeling [33].
In the current work, we take advantage of coupled chaos to study the most basic financial assumption revision around the financial theory of speculation, by studying a basic adaptive speculation dynamics, under Lo’s AMH, in a multiple asset market characterized by coupled stochastic chaotic maps, with a feedback between speculator impact on logarithmic returns and volatility, leading to a complex coevolutionary dynamics between speculation and volatility risk in a multiple asset market.
As stressed, deterministic chaos and stochastic chaos are not mutually exclusive, so that one may have a noisy nonlinear system that would behave as a deterministic chaotic oscillator if the noise was removed, such a system may exhibit sensitive dependence upon initial conditions that can amplify noise-related fluctuations, it can also lead to the noise-induced order phenomenon [34].
Stochastic chaotic maps, in turn, allow one to model open chaotic systems where there is a coupling to high-dimensional noise, which makes them effective models for dealing with complex adaptive dynamics which include endogenous responses with sensitive dependence to initial conditions and complex responses to external noise. Non-trivial dynamics occur when such coupling is introduced, as we will be seeing in the current work in the financial application context.
By extending the single stochastic chaotic map to the coupled maps’ context, we are led to a coupled stochastic chaos model, the spatial coupling associated with coupled chaotic maps also involves, in this case, a complex nonlinear co-evolutionary dynamics with respect to the noise itself, leading to another level in networked chaos theory, with relevance for complex systems modelling. In the current article we will compare the coupled stochastic chaotic map with the coupled deterministic map model and also research how microscopic noise can affect the coupled market dynamics in regards to inter-asset synchronization dynamics.
Single Asset Model and an Adaptive Theory of Speculation
As reviewed in the previous section, the foundational mathematical model of financial price dynamics was introduced by Bachelier, who proposed a theory of speculation which assumed a driving Gaussian independent and identically distributed noise term, justified on account of speculation being associated with a maximal diversity of information in such a way that speculators operated independently from each other and randomly, compensating for each other’s moves leading to the final Gaussian structure as a limit distribution.
The model was eventually corrected to account for nonnegative prices, leading to the lognormal probability model for financial price dynamics, the Geometric Random Walk model (in discrete time) (GRW) and the Geometric Brownian Motion (in continuous time) (GBM). The main behavioral assumptions underlying speculative dynamics in financial markets assumed by Bachelier were still valid for the justification of the GRW and GBM models, namely, that speculators operate independently and randomly so, in this way forming beliefs on a diversity of information that leads to a probabilistic balancing of the reasons for buying and selling, so that speculators’ impact on the market’s logarithmic returns should be probabilistically modelled by a Gaussian distribution, centered around a mean.
Formally, in discrete time, this leads to a model of price fluctuations such that the price of a financial asset is described by the equations:

where r0 is an average returns rate, σ is a fixed volatility parameter and x(t) is an Independent and Identically Distributed (IID) Gaussian noise term x(t) ~ N(0,1) , which incorporates the speculation impact on financial returns and corresponds to a speculation impact variable, the size of this impact being determined by the scale factor set by the fixed volatility parameter.
The problem with this model, as reviewed in the previous section, is that it does not capture actual market dynamics, more specifically, it does not capture financial market turbulence, which is empirically observed in actual financial returns, a point that was stressed by Mandelbrot, and which included the identification of volatility clustering, excess kurtosis, nonlinear dynamics, power law decay in the distribution of squared logarithmic returns and multifractal scaling in financial data, these findings influenced, as reviewed in the previous section, the complexity approaches to financial theory and the linked econophysics research lines to search for possible sources of the turbulence and multifractal scaling.
Indeed the GRW/GBW models do not produce the volatility clustering, the high price jumps and even speculative bubbles and crashes. Volatility clustering, nonlinear dynamics, speculative bubbles and crashes presuppose a collective dynamics that is not consistent with Bachelier’s hypothesis of speculators randomly trading in an independent way.
The fluctuations that include volatility clustering, high price jumps, bubbles and crashes as well as excess kurtosis with respect to the Gaussian distribution, along with the evidence of multifractal scaling and long memory in the squared returns, as well as power law decay in the distribution of the squared returns imply the presence of some type of underlying nonlinear dynamics associated with financial trading in which the speculation impact variable and volatility may be coupled, with volatility being a time variant variable .
Returning to Bachelier’s original proposal and looking at speculative dynamics, the turbulence signatures reviewed above indicate the need for a revision of the assumption that speculators operate independently as uncorrelated individuals forming beliefs on a diversity of information that leads to a probabilistic balancing of the reasons for buying and selling. Instead, the formation of speculative trends and market corrections, including the possibility of formation of speculative bubbles and crashes, is more consistent with Lo’s Adaptive Market Hypothesis (AMH), under which the market is assumed to work as a Complex Adaptive System (CAS) and should be modelled as such [22].
Revising Bachelier’s original assumption, under Lo’s AMH framework, one needs to consider a collective nonlinear adaptive dynamics by speculators that can lead to speculative buildups driving market upwards or downwards, trends that are broken by market corrective movements, this coevolutionary dynamics is also present in business cycle models that include accelerator with adaptive components that lead to a reversal in an upward or downward trend, an example of which is the cubic model addressed in a macroeconomic context which includes cyclical buildups and contra-cyclical adaptive responses and can lead to chaotic dynamics in the business cycle [35].
However, the cubic map model of business cycles, while able to capture buildups and corrective market movements is insufficient, we need to consider the link between the speculative trends and market corrections with the processing of risk, that is, we need to include the impact in volatility of the speculative dynamics as well as a possible feedback from volatility on speculative dynamics, the application of the cubic map in a multi-asset market also needs to transition from a decoupled to a coupled nonlinear map. In the present section, however, we address the single asset model, studying its properties and, then, expand it to a multi-asset framework building an artificial financial market where N companies’ shares are traded on the market, leading to a globally coupled nonlinear model, indeed, to better study the coupled model, we need to study first the properties of the single asset model.
In the single asset model, we revise the logarithmic returns equation replacing equation (2) with the following:

In this case, we get a time varying volatility σ (t)multiplied by x(t)which, keeping with Bachelier’s root, is the main dynamical variable for the impact of speculation on financial returns, the speculation impact variable, in turn, coincides with the volatility adjusted excess returns for the trading round:

In this way, while, in the GRW, there is a fixed impact size of speculation on the financial logarithmic returns, given by a fixed volatility parameter σ , in equation (3) this impact size is time varying. This correction is common in time varying volatility models including the Generalized Autoregressive Conditional Heteroskedasticity (GARCH) models [5]. There are two possible assumptions, one is that σ (t) is independent of the speculation impact dynamical variable, the second is a dependence of σ (t) upon that dynamical variable, as assumed, for instance, in heteroskedasticity models like the GARCH models, these models, however, show a cutoff in the memory, not capturing the power law signatures and multifractal scaling as stressed.
From a theoretical standpoint, the dependence of σ (t) on x(t) means that the speculative dynamics not only affects returns through the main speculation impact variable x(t) , but it also affects the dynamical volatility variable σ (t) which, in turn, determines the size of the speculation impact on logarithmic returns, this is especially linked to trading volume and market orders which lead to a time-varying impact of the speculation impact variable x(t) on the logarithmic returns. In turn, it is reasonable to assume that there is a processing of volatility risk by speculators which may lead to a feedback from the volatility variable to the speculation impact variable, a feedback that, as per equation (4), affects each trading round’s volatility adjusted excess returns. To capture this coevolutionary dynamics we need a coupled nonlinear map that works with this feedback.
The model that we study is a stochastic nonlinear dynamical model, x(t) where incorporates speculative trend reinforcement dynamics and market correction dynamics, which is consistent with the AMH when applied to a speculator-driven market, the volatility variable is, in turn, given by a fixed scale factor multiplied by a second dynamical variable that contains an autoregressive component but that also depends upon x(t) . Below are the single asset main equations, which we now analyze from a financial standpoint.

where w(t) is uniform IID noise w(t) ~U(−1,1) and x(t)∈[−1,1].
In order to explain the model and understand its dynamics from
a financial standpoint, let us consider first the special case where
b1 = 0 and l = 0, in this case, there is no stochastic component, and
the dynamics for the speculation impact variable is given by the
cubic map  which incorporates speculative trend
and self-correction cycles leading to cyclical and contra-cyclical
adaptive responses and exhibits chaotic dynamics. The volatility
is, in this case, driven by the chaotic dynamics of the speculation
impact variable x(t) with no feedback to x(t) . An example of the
map for b0 = 3 is shown in Figure 1.
which incorporates speculative trend
and self-correction cycles leading to cyclical and contra-cyclical
adaptive responses and exhibits chaotic dynamics. The volatility
is, in this case, driven by the chaotic dynamics of the speculation
impact variable x(t) with no feedback to x(t) . An example of the
map for b0 = 3 is shown in Figure 1.

Figure 1: Cubic map for b0 = 3 .
To understand the map’s dynamics from a financial standpoint we need to consider the map’s two inflection points:

Given the two inflection points, we can analyze the different
regions of values for the map. The first two relevant regions are  , these are trend reinforcing
regions, in the sense that if the value of x(t −1) is negative then
so will be the value of x(t) , with x(t) decreasing with x(t −1)until
the minimum is reached at x− , likewise, for
, these are trend reinforcing
regions, in the sense that if the value of x(t −1) is negative then
so will be the value of x(t) , with x(t) decreasing with x(t −1)until
the minimum is reached at x− , likewise, for  is
positive and grows with x(t −1) until the maximum is reached at
x− , given the dependence of the returns on x(t) , as per equation
(3), this means that the financial returns are driven by the trend
reinforcing dynamics, in these two regions.
is
positive and grows with x(t −1) until the maximum is reached at
x− , given the dependence of the returns on x(t) , as per equation
(3), this means that the financial returns are driven by the trend
reinforcing dynamics, in these two regions.
For the region  we get a market reversal dynamics,
such that x(t) grows with decreasing x(t – 1) and decreases with
increasing x(t–1) which incorporates a trend reversal dynamics, a trend reversal profile is also obtained for
we get a market reversal dynamics,
such that x(t) grows with decreasing x(t – 1) and decreases with
increasing x(t–1) which incorporates a trend reversal dynamics, a trend reversal profile is also obtained for  . Finally, when x(t −1) = 0 so is x(t), that is, x(t −1) = 0 is a fixed point of the map.
. Finally, when x(t −1) = 0 so is x(t), that is, x(t −1) = 0 is a fixed point of the map.
In Figure 2, we show a simulation of the financial returns, with , b0 = 3 illustrating how the single asset model can already generate turbulent market dynamics without any external noise term.

Figure 2: Simulated logarithmic returns r(t) (left) and time varying
volatility s (t) (right), 100,000 iterations after 10,000 iterations
removed for transients, uniformly randomly chosen initial conditions,
The emergence of the usual turbulence markers, including volatility clustering (volatility bursts) and large jumps in the returns, can be seen in the model’s simulation. Thus, the model shows how financial turbulence can emerge endogenously under a basic speculation reinforcement and correction dynamics. There are various power law signatures associated with the generated financial series in regards to volatility risk and tail risk for Figure 2’s simulation.
First of all, the estimated Fisher’s kurtosis for Figure 2 simulation is 19.766319, with zero kurtosis being the reference for a Gaussian distribution, and the Jarque-Bera test of normality applied to the financial returns gives a test statistic of 162778.780642 and a p-value of 0.0, which means that there is a statistically significant deviation from the Gaussian distribution due to excess kurtosis, which is one of the stylized points of actual financial markets.
Therefore, when we depart from the assumption of randomly independently trading speculators to include speculation collective trends and market correction associated with a theory of speculation dynamics as an adaptive dynamics, a theory that is consistent with Lo’s AMH, then, we find that the basic nonlinear dynamics associated with this speculation adaptive dynamics, and its nonlinear impact in volatility, can lead to a chaotically driven volatility and endogenously generate excess kurtosis.
However, excess kurtosis is not the only marker in financial market turbulence, another marker is the power law decay of the statistical distribution of squared logarithmic returns r2 (t) , which are used as an observable measure of financial volatility, such a power law decay is linked to a fractal structure in the distribution of the squared logarithmic returns and is one of the markers of SOC in the financial markets dynamics, as reviewed in the previous section.
In this case, we find that the squared returns for Figure 2’s simulation exhibit evidence of a power law scaling in their statistical distribution; this is shown in Figure 3 (left) which is a plot of the histogram with the logarithm of the bin centers versus the logarithm of the relative frequencies. In Figure 3 (right), we also show the log-log plot of the histogram for the time-varying volatility , which also shows a convergence to power law decay. These are not, however, the only power law signatures, indeed, the power spectrum of the volatility variable also shows a power law decay with increasing frequencies (Figure 4), another feature of SOC.

Figure 3: Histograms calculated for the squared returns r2 (t) (left) and s (t) (right), plotted on a doubly logarithmic scale for the class centers versus frequencies, calculated on Figure 2’s simulation.

Figure 4: Power spectrum of the volatility variable s (t) from Figure 2’s simulation.
The simulation illustrated in Figures 2-4 provides an example of the registered SOC features in finance reviewed in the previous section, the simulation also produces as we will now see emergent multifractal signatures in the returns signal.
While power law signatures are consistent with actual financial turbulence, this turbulence has also shown evidence of multifractal scaling, which led Mandelbrot to propose that financial turbulence has an underlying multifractal dynamic. Indeed, one of the peculiar traits of financial returns is the emergence of longmemory in market observable volatility measures like the squared returns, which could point to a unifractal scaling associated with this measure, Mandelbrot, however, identified the presence of multifractal scaling rather than a unifractal process in financial data, a feature that was further confirmed by different authors and that points to the financial market operating as a nonlinear dynamical system with multifractal scaling.
The presence of multifractal scaling can be analyzed through different methods; the method we use here is Multifractal Detrended Fluctuation Analysis (MFDFA) with polynomial fitting [36]. Due to its implications in terms of interpretability regarding algorithmic financial risk measurement over different investment horizons, a point that we will return to as we review this method. In the MFDFA, given a time series with T data points, we can calculate the cumulative sums, for t=1,2,…,T:

Where is the sample average taken over the T periods.
The second step is to section the data into non overlapping
segments of length s , leading to  segments [36].
Since the dataset size is not always a multiple of the segment’s
length one needs to discard the last data points and then apply the
same procedure but to the first data points leading to
segments [36].
Since the dataset size is not always a multiple of the segment’s
length one needs to discard the last data points and then apply the
same procedure but to the first data points leading to ![]() segments
[36] to which one fits a polynomial
segments
[36] to which one fits a polynomial  of order
of order  and calculates the
difference of the data to the polynomial fit leading to the variance
function:
and calculates the
difference of the data to the polynomial fit leading to the variance
function:

From a financial standpoint, polynomial fitting to different segments of a series captures an important point which is the ability for basic trend following algorithms to capture information in data.
Now a q-th order fluctuation function can be extracted by averaging over the variance functions values evaluated for each length s interval, leading to:

If the data exhibits power law correlations, these can be uncovered
by studying the log-log plot of  with respect to S , studying the
presence of power law scaling of the form:
with respect to S , studying the
presence of power law scaling of the form:

where h(q) are the generalized Hurst exponents.
If the data is monofractal, these exponents will be fixed, all parallel lines in the log-log plot have the same slope or at least will not vary much with respect to the series’ main scaling so that h(q) will either all coincide with each other or, at least, fluctuate in a small interval around the true scaling exponent which is the Hurst exponent or Hurst index H. Multifractal dynamics is visible in the power law scaling exhibiting different slopes in the log-log plot, and a generalized Hurst exponent scaling over a wider rage. Linked to generalized Hurst exponents are the scaling exponents:

The above algorithm is the MFDFA with polynomial fitting. Using the squared returns as a basic volatility measure and the source signal for the above multifractal analysis, the analysis up to the calculation of the variance function provides for a relevant financial point. First of all, the cumulative deviations provide for a sum of deviations between the squared returns over an investment period t and the average sample volatility measured in terms of the mean squared returns over the T sample periods:

Large cumulative deviations are expected to occur in turbulent periods associated with volatility clustering and large price jumps. A prediction of these cumulative deviations provides for an attempt at anticipating transformations in volatility risk, in this sense, the polynomial fitting can be seen as a basic benchmark algorithm for predicting cumulative deviations over transaction horizons, with these transaction horizons being defined in terms of the size s of the sample segments.
Now, in this case, the variance function, described in equation (13) provides for a measure of dispersion with respect to the predicted cumulative deviations in volatility risk and is, in itself, a risk measure associated with market volatility in each segment.
The q-th order fluctuation function, in turn, when calculated for the squared returns provides for a risk measure calculated for the original squared returns signal over different scales defined by the order, in this sense, the link between multifractal scaling signatures and market volatility risk are captured in the MFDFA analysis, with polynomial fitting operating as a basic benchmark for a volatility risk trend following algorithm that uses the squared returns as a reference for dynamical volatility measurement.
In Figure 5, we show the plot of the estimated fluctuation function, the corresponding generalized Hurst exponents, the scaling exponents and the histogram of the generalized Hurst exponents calculated for the squared returns r2 (t) of Figure 2’s simulation.

Figure 5: Estimated fluctuation function (top left), generalized Hurst exponents (bottom left), scaling exponents (top right), histogram of the generalized Hurst exponents (bottom right), calculated for the squared returns of figure 2’s simulation.
As shown in Figure 5, there is a power law scaling at different lags, characterized by different slopes in the log-log plot of the fluctuation function, a point that is further reinforced by the histograms, indicating that the squared returns series is not monofractal, instead exhibiting different slopes, therefore different exponents, this can be further confirmed by looking at the generalized Hurst exponents. In the plot of the exponents versus the order (Figure 5 bottom left) the exponents rise exponentially from negative orders to positive orders, achieving a peak at positive order and then decreasing. The histogram, while showing a dominance of lower exponents, also shows a rise for higher exponents.
Now, this dynamics was generated for the model without the volatility feedback on the speculation impact variable, that is, with b1 = 0 and also without the noise coupling, before proceeding to the multi-asset model, we need to consider the impact of the volatility feedback and of the noise coupling. We begin by addressing the volatility feedback with no noise and then study the effects of noise coupling, which lead to a stochastic chaos model of adaptive speculation dynamics.
From a financial standpoint, the volatility feedback is justified, in the sense that volatility may impact trading decisions and speculative movements, in the case of the present model, with no noise coupling, the volatility feedback leads to the following dynamical equation for the speculation impact variable:

We have a weighted average between the cubic map, in which the cube of the speculation impact variable appears with a negative factor, and a volatility modulated term that results from the product of σ (t−1) and x3 (t−1) , the higher the volatility the greater the positive impact of x3 (t−1) . This term is trend reinforcing with respect to speculative dynamics and accelerates both for negative and positive values of x(t−1)with a greater impact depending upon the volatility σ (t−1) .
In this sense, there is a weighted average between the adaptive dynamics associated with speculative trends formation and market corrections with trend reversal, which is incorporated in the cubic map, with an associated weight of 1− b1 , and a speculative trend reinforcing term which is associated with the volatility modulated impact of x3 (t−1) , with an associated wight of b1 .
While, at first sight it might seem that this would lead to a greater volatility, the actual effect is that the market becomes less volatile, which means that the volatility feedback ends up operating as a turbulence dampener; this is linked to the impact of the coupling on the bifurcations structure of x(t) . Indeed, as is shown in Figure 6, the effect of increasing volatility coupling is a progressive shift of the bifurcation plot to the right, both for positive and negative initial conditions, since the two are plotted in Figure 6. As a consequence of the shift, the chaos region of the cubic map becomes progressively smaller until all chaos is suppressed.

Figure 6: Bifurcation plots for x(t) , b0 from 0 to 3, for different values of b1 . x(0) Randomly chosen with uniform distribution in (0,1) with bifurcations plotted along with its symmetric −x(0) also plotted, 
The chaos suppression is not the only relevant point, the dependence on the sign of the initial value and its implication for the financial dynamics is also relevant. Indeed, in Figure 7, we show two bifurcation diagrams for x(t) , zooming in on the chaos region; the top diagram is for b1= 0 the bottom is for b1 = 0.1.

Figure 7:Bifurcation plots for x(t) with varying b0 from
2 to 3, for b1 = 0 (top) and 1 b = 0.1 (bottom). In blue is
represented a positive initial condition, in red it’s symmetric, 
The diagrams represent in blue color the value of a positive initial condition and in red its symmetric, the diagrams show that if the initial condition is positive the period doubling route to chaos leads to a wide region of chaotic fluctuations for x(t) , interrupted by periodic windows, fluctuating in a positive values band, which means that the returns will only be positive. For the symmetric initial condition, which is negative, the period doubling route to chaos leads to a mirror image of chaotic fluctuations, in this case, fluctuating in a negative values band, which means that the returns will only be negative. There is a threshold, however, for the cubic map’s parameter b0 beyond which the two initial conditions’ regions of fluctuations overlap, leading to a fluctuation over both positive and negative values x(t) of for both initial conditions.
As the volatility coupling parameter is increased, the progressive translation to the right of the bifurcations structure leads to a reduction of this region. There is a point of increasing values of the volatility coupling parameter beyond which the bifurcations of x(t) lead to a complete separation between the two regions which means that the negative initial condition will lead only to negative returns and the positive initial condition will lead only to positive returns. Thus, from a financial standpoint the volatility feedback on the speculation impact variable x(t) cannot be too large in order to lead to positive and negative fluctuations.
Another point about the coupling is that the bifurcation structure of the volatility gets displaced to the right in tandem x(t) with ’s bifurcations, as shown in Figure 8 where the dynamics of ln(σ (t)) are plotted for different values of b0 obtained from the same data as Figure 7, which plots the volatility variable in logarithmic scale for a better visualization.

Figure 8: Bifurcation structure for ln(s (t)) obtained from Figure 7’s computation, the purple color results from the coincidence of the blue (positive) and red (negative) initial conditions.
The displacement of the bifurcation structure to the right is again
visible, the reason for this displacement and reduction of the
regions of chaos is due to the fact that as the volatility coupling
increases (increase of b1 ) the bifurcations of x(t) conserve the
basic structure but are delayed, leading to the displacement to the
right effect, with a reduction of the chaotic region, in the volatility
variable, the consequence is a reduction in the fluctuations of u(t) and, hence, of  , which means that the market will show
a reduction in turbulence, this can be seen in Figure 8.
, which means that the market will show
a reduction in turbulence, this can be seen in Figure 8.
Now, the presence of noise leads to a stochastic chaos model, with two effects on x(t) , one is that, for a sufficiently high noise coupling, periodic windows are destroyed, the second is that the superposition of the negative and positive initial conditions fluctuations starts at lower values of the parameter b0 as is shown in Figure 9.

Figure 9: Bifurcation plots for x(t) with varying b0 from 1.6 to 3, for l = 0.01, 0.025 and 0.05. In blue is
represented a positive initial condition, in red its symmetric,
The impact of noise on the financial returns dynamics is, in turn, nontrivial, in the case of a leptokurtic turbulent market dynamics, we find that the noise tends, initially, to reduce the kurtosis but as the noise coupling is increased the kurtosis starts to increase exponentially, this is illustrated in Figure 10, with b1 = 0.1, and 2.9 b0 = , in the Figure it is shown the average kurtosis for 100 simulations of 100,000 steps each, after 10,000 initial steps being dropped for transients, and each initial condition being randomly chosen with uniform distribution over the variable’s fluctuation range ((-1,1) for x(t) and (0,1) for u(t) ). A large enough noise coupling can produce an explosive behavior and lead to overflow divergence.

Figure 10: Average kurtosis obtained with l ranging from 0 to 0.12
in steps of 0.01, in each case the average kurtosis values for the
returns’ distribution were obtained for 100 simulations with random
uniformly chosen initial conditions, each simulation comprised of
100,000 iterations, after 10,000 iterations dropped for transients, 
Also, the average value of the kurtosis in repeated simulations rises exponentially with b0 approaching 3, as is shown in Figure 11 for a noise coupling l=0.07, where we find the presence of three dynamical regimes, a platykurtic regime, a leptokurtic regime with kurtosis rising with b0 , leading to markets with increasingly turbulent returns, and a transition between the two regimes which is nearly Gaussian on average.

Figure 11: Average kurtosis obtained for b0 ranging from 2.61 to
3 in steps of 0.001, in each case the average kurtosis values for the
returns’ distribution were obtained for 100 simulations with random
uniformly chosen initial conditions, each simulation comprised of
100,000 iterations, after 10,000 iterations dropped for transients, 
In this case, the GRW’s Gaussian dynamics is recovered with adjustment of the parameter b0 , but it depends upon the initial conditions, thus, for instance, while 2.64152 b0 = led to a close to an average kurtosis estimate of 0.000217 in 100 simulations with the same parameter set as that of Figure 11, which is close to the normal distribution for the logarithmic returns, the maximum kurtosis obtained in the 100 simulations was 0.319141 and the minimum was -0.103179, which is a wide range of values.
A key parameter that sets the scale for the volatility fluctuations is v3 , which is associated with the interaction term between the previous round’s volatility dynamical component u(t −1) and the round’s speculation impact variable, indeed, if we increase beyond a certain level we get the usual market turbulence with the power law scaling markers and multifractal signatures and a too high value of may lead to very high jumps or even a blow up in the computations, especially with rising noise levels. The values for which this divergence occurs depends upon the parameter o b , thus, for instance, we already obtain blow up dynamics and overflow errors for b0 =3 , v3 =1.9 and a noise level l equal to 0.08.
The kurtosis scales exponentially with v3 , as illustrated in Figure 12 for different values of the parameter both without and with different noise coupling levels.

Figure 12: Average kurtosis obtained for l=0, 0.05, 0.1, v3 ranging
from 0 to 2 in steps of 0.1, the average kurtosis values for the
returns’ distribution were obtained for 100 simulations with random
uniformly chosen initial conditions, each simulation comprised of
100,000 iterations, after 10,000 iterations dropped for transients, 

As shown in Figure 12, the dynamics can, again, be classified in three regimes, the platykurtic regime, the leptokurtic regime and a transition between both which leads to nearly Gaussian dynamics with the Fisher’s kurtosis transitioning from negative to positive and from a non-turbulent market to a progressively more turbulent market.
The Gaussian structure, which recovers the Gaussian assumption of the GRW model is thus also present in this case as a transitional regime between the platykurtic and the leptokurtic power law scaling volatility, contrasting, however, with the previously analyzed mesokurtic transition that occurs with a variation of b0 , this transition occurs with smaller dispersion, indeed, as an illustration, for the same parameters as in Figure 12, when v3 =1.1651, in 100 simulations with initial conditions randomly chosen, each time, with uniform distribution over the variables’ fluctuation ranges (-1,1) for and (0,1) for x(t) , we got an average kurtosis for u(t) the returns of 0.001035, a maximum p-value of 0.999661 for the Jarque-Bera normality test applied to the returns distribution and a minimum p-value of 0.013193, which is not statistically significant at the 1% significance level, showing the predominance of the Gaussian as a transition distribution between the platykurtic and the leptokurtic turbulent regime.
In Figure 13, we show a simulation of the returns with v3 =1.1651 , zero noise coupling, and the remaining parameters as those of Figure 12.

Figure 13: Logarithmic returns obtained from a 100,000 iterations
simulation of the single asset model after 10,000 iterations removed
for transients, uniformly randomly chosen initial conditions, 
The estimated Jarque-Bera test statistic, for Figure 13 data is 0.515714 and the p-value is 0.772706, which means that we get an approximately Gaussian distribution for the financial returns, in this case, however, we do not have the standard GRW driven by Gaussian IID noise, even though the returns do follow a Gaussian distribution, indeed, rather than IID noise, the system’s dynamics are being driven by a deterministic chaotic attractor as shown in Figure 14, which resembles Cheshire Cat’s smile, this structure we will show, will be key to understand the source of turbulence in the returns.

Figure 14: Attractor for the speculation versus volatility variable obtained from a 200,000 iterations simulation with the same parameters and initial conditions as Figure 13’s simulation.
In Figure 15, we show another attractor, in this case for b0 =3 and v3 =1.31, which leads to an approximately Gaussian distribution for the logarithmic returns, with a Jarque-Bera test statistic value of 2.698160 and a p-value of 0.259479. Again, we have the smile structure.

Figure 15: Attractor for the speculation versus volatility variable
obtained from a 200,000 iterations simulation, after 10,000 iterations
removed for transients, uniformly randomly chosen initial conditions, 
These two examples, while leading to shapes that have a few differences, both share the general shape of a smile, such that, for intermediate values of x(t) , the volatility parameter σ (t) is smaller, increasing as x(t) tends to its maximum and to its minimum values. The seed for the observed turbulence lies here, since, as v3 is increased, this attractor shape is distorted with the intermediate level contracting and the extremes expanding in volatility values, which leads to the returns jumps and laminar phases. This contraction is illustrated in Figure 16, where we increase the values of v3to the turbulence region.

Figure 16: Attractors for the speculation versus volatility variable
obtained from 200,000 iterations simulations of the single asset model,
after 10,000 iterations removed for transients, with the same initial
conditions as in Figure 14, with v3 = 2 (left) and v3 = 2.2 (right), 
Figure 16 shows the compression of the attractor’s middle section with the high volatility dispersion in the extremes, in the case of Figure 16(right), we get an estimated sample kurtosis of 37.032034, a Jarque-Bera test statistic of 40042650.407619 and a p-value of 0.0.
While the rise in the parameter v2 also leads to a rise in kurtosis, its effect is a rescaling of the attractor with a smaller impact in the volatility, not leading to the turbulence features in the returns, as shown in Figure 16, this is because the rise in the parameter v3 leads to a sharp compression of the middle section, and expands the extremes leading to the jumps, the compression reinforces laminar phases while the expansion reinforces the large jumps.
Now, the effect of the noise coupling on the leptokurtic turbulent regime is also the reduction of the middle section with the expansion of the extremes, which explains the volatility amplification shown in Figure 10. This effect is illustrated in Figure 17. In this sense, of the two parameters associated with the dependence of the volatility variable σ i (t) = c.ui (t) on the speculation impact variable x(t) , v3 is a key parameter in setting the scale for excess kurtosis and turbulence, another relevant parameter is v1 .

Figure 17: Attractors for the speculation versus volatility variable
without noise and with 0.1 noise coupling, from a 200,000
iterations simulation, after 10,000 iterations removed for
transients and random uniformly chosen initial conditions, 
Table 1 illustrates the impact of rising v1 for two values of b0 showing the rise in average kurtosis from rising values of v1
| v1 | b0 = 2.9 | b0 = 3 |
|---|---|---|
| 0 | 0.77413 | 0.607 |
| 0.05 | 1.04309 | 0.86239 |
| 0.1 | 1.45656 | 1.28795 |
| 0.15 | 2.16738 | 1.9362 |
| 0.2 | 3.56075 | 3.25828 |
Table 1: Average kurtosis obtained for rising values of v1 , b0 = 2.9
and b0 = 3 , and 100 simulations each with random uniformly chosen
initial conditions, 100,000 iterations, after 10,000 iterations dropped for
transients, 
The v1 parameter is related to an autoregressive volatility component, in this case, the autoregressive component leads to a rise in the Fisher’s kurtosis. In the next section, we will also see the relevance of the parameter v1 in setting the impact of the autoregressive component in u(t) ’s dynamics and influencing the kurtosis with impact on the financial returns’ mean field. Having addressed the single asset’s main features, we now introduce the multi-asset market and study the effects of global coupling.
Multiple Asset Model
Considering a market comprised of N companies operating in the same industry with traded common stocks, we transition to a multiasset artificial financial market, in this case, we need to include a global coupling in the speculative dynamics. Globally coupled maps constitute the simplest example of a network of chaotic elements exhibiting a dynamic many-to-many relation; it is also a useful model in social, economic and financial applications of chaos theory.
In the present case, since we are dealing with a market of N competing companies, the global coupling is sound and, in our model, it is associated with common industry-wide speculative dynamics, implying multi-asset positions and portfolio reconfigurations as well as expressing common collective factors affecting an industry’s shares’ values, reflected in collective speculative motions. In the chaotic regime, the global coupling of chaotic oscillators introduces a tension between microscopic chaotic divergence and macroscopic mean field driven synchronization.
Extending from the single asset model, each company’s logarithmic returns are characterized by the dynamical equation:

for , with the speculation impact variable now characterized by the globally coupled nonlinear map:

Due to the dependence of the time varying volatility component xi (t) upon ui (t) which follows a globally coupled nonlinear map with mean field coupling, the volatility dynamics will be nonlinearly affected by the mean field, by way of the squared value of xi (t) . The map g(xi (t-1)) is the single asset map studied in the previous section, which incorporates an asset specific stochastic chaos dynamics, the mean field coupling, in turn, decomposes as follows:

Therefore, we have a deterministic component for a globally coupled map of N chaotic oscillators plus a factor that depends upon the sum of N independent and identically distributed uniform noise terms, this means that, at the “microscopic” level (the market for the company’s shares), there is the local stochastic chaos driver given by the noisy nonlinear map g which has a weight of 1−ε but the speculative dynamics also depends upon a collective dynamics associated with the market for the N companies’ shares, this coupling also includes a deterministic and noisy component and incorporates industry-wide common speculative trading actions, which also affect volatility through xi2 (t) , leading to a complex feedback network between local speculative dynamics, volatility dynamics and the industry-wide speculative motions, with both local speculation impact variables and volatility affecting the speculation impact variable mean field and the speculation impact variable mean field, in turn, affecting each local speculation impact variable and volatility.
To characterize the global financial dynamics we will analyze another mean field, which is the logarithmic returns’ mean field, corresponding to the average of the logarithmic returns at each trading round, allowing us to characterize the mean returns dynamics:

Considering first a noise free market, with l=0, which leads to a standard deterministic globally coupled network of chaotic oscillators, in Figure 18, we show a simulation of the mean field for the logarithmic returns with no global coupling and small global coupling.

Figure 18: Simulated returns mean field for N = 10 companies,
no global coupling (left) and global coupling of 0.01 (right),
100,000 iterations shown, after 10,000 initial iterations removed
for transients, the same randomly chosen initial conditions
on the left were used on the right for comparison purposes, 
With no global coupling the market exhibits large swings in prices but no turbulence markers (Figure 18 (left)), with a small coupling of just 0.01, the mean field dynamics changes to the usual turbulent market dynamics, with jumps at multiple scales (Figure 18 (right)), the kurtosis in this case goes from 0.409493 (Figure 18 (left)) to 70.084854 (Figure 18 (right)).
In the first case, the squared value of the logarithmic returns mean field’s distribution does not exhibit a power law decay, decaying faster than the power law Figure 19, in the second case we find the presence of the usual power law decay (Figure 19 (right)) with the fitted slope of -2.988916 and an R2 = 0.979940 , also exhibiting multifractal signatures (Figure 20). The transition to turbulence can be explained at the single asset level, indeed, at the company level, for a randomly chosen company, when ε = 0 , the simulation parameters lead to the attractor for the local speculation and volatility variables shown in Figure 21 left, however, when the attractor is changed to the one shown in Figure 21 right, which shows a number of features that explain the turbulence.

Figure 19: Histograms calculated for the squared value of the logarithmic returns’ mean field of Figure 18 with no global coupling (left) and 0.01 global coupling (right), plotted on a doubly logarithmic scale for the class centers versus frequencies, calculated on Figure 18’s simulations.

Figure 20: Fluctuation function (left), generalized Hurst exponents (right) estimated on Figure 18 (right)’s simulation data for the squared value of the logarithmic returns’ mean field.

Figure 21: Attractors for the speculation versus volatility variable of a local randomly chosen company, in Figure 18’s simulation, the left figure shows the dynamics without global coupling and the figure on the right shows the dynamics with 0.01 coupling.
First, there is, at the company level, the compression of the
fluctuation region with a concentration of volatility fluctuations,
which account for laminar periods, then, there are two divergence
bands, one neari  and another one at the extremes of xi (t ) , these two regions show that the market can jump in volatility
for intermediate values of the speculation impact variable and for
extreme values of the speculation impact variable. Once more,
a compression of the chaotic attractor with divergence bands is
shown to be the source of the turbulent dynamics.
and another one at the extremes of xi (t ) , these two regions show that the market can jump in volatility
for intermediate values of the speculation impact variable and for
extreme values of the speculation impact variable. Once more,
a compression of the chaotic attractor with divergence bands is
shown to be the source of the turbulent dynamics.
While low coupling can lead to turbulence, high coupling can recover the initial attractor, for instance, a 0.55 coupling is enough to recover the uncoupled attractor shown in Figure 21, leading locally to the same attractor shape as in Figure 21(left), this is the case for higher global coupling values with no noise. With noise coupling, however, turbulence resurfaces as shown in Figure 22, for a noise coupling of 0.025 and a global coupling of 0.55, the estimated sample kurtosis for the mean field of the logarithmic returns is of 375.406009, showing an excess kurtosis.

Figure 22: Simulated returns mean field for N = 10 companies, with 100,000
iterations shown, after 10,000 initial iterations removed for transients, 
While, in the above case, the increase in global coupling between companies’ trading recovers and reinforces the initial attractor, with noise coupling being the source of turbulence, this is not always the case, namely, for other parameters, higher global coupling does not recover the initial dynamics and can lead to turbulence, this occurs in Figure 23, where we simulate the external noise free market with b1 = 0.1, v3 = 2.1, no noise coupling and the remaining parameters as those of Figure 18, we find, in this case, a clear difference as a consequence of high coupling, where high coupling, instead of recovering the non-turbulent attractor, leads to global financial returns turbulence and changes the squared value of the logarithmic returns’ mean field’s distribution to a power law scaling distribution, with an estimated slope of -3.537517 and an R2 of 0.990442, without any noise coupling involved.

Figure 23: Simulated returns mean field for N=10 and respective
histograms for its squared value with class centers plotted versus
the relative frequencies plotted in log-log scale, e = 0 (left),
e = 0.7 (right), 100,000 iterations shown, after 10,000 initial
iterations removed for transients, the same randomly chosen initial
conditions on the left were used on the right for comparison, 
We also find a difference in the multifractal spectra associated with Figure 23’s simulations, while, in both cases, there is evidence of multifractal scaling for the squared value of the logarithmic returns’ mean field, for the 0.7 coupling we get a wider range of slopes in the fluctuation function, while the zero coupling exhibits more parallel lines, as shown in Figure 24. With the zero coupling there is an increasing sigmoid curve in the generalized Hölder exponents, while the 0.7 coupling leads to a decrease for higher lags (Figure 24 in the right).

Figure 24: Fluctuation functions and generalized Hurst exponents estimated on Figure 23’s simulation data for the squared value of the logarithmic returns’ mean field.
Low versus high global coupling, in this last case, also affects the dynamics with respect to the parameter v2 , with low coupling leading to a fluctuation of the kurtosis around 3 with increasing values of v2 , while for high coupling we get higher kurtosis values and an exponential increase in this kurtosis with increasing values of v2 , as illustrated in Table 2, therefore, the sensitivity profile to the parameter v2 can change for different combinations of parameters.
| v2 | ε = 0.01 | ε = 0.7 |
|---|---|---|
| 0.01 | 6.04217 | 17.3715 |
| 0.02 | 2.31133 | 18.0164 |
| 0.03 | 2.99802 | 22.9131 |
| 0.04 | 3.74571 | 45.201 |
| 0.05 | 3.64901 | 58.8756 |
Table 2: Sample kurtosis for different values of v2 , ε = 0.01 and ε = 0.7 , with the remaining parameters and initial conditions equal to Figure 23.
The autoregressive parameter also plays a key role in setting the scale for turbulence, similarly to v3 , indeed, increasing values of the parameter leads to an exponential rise in kurtosis, especially as the parameter approaches the value 0.2, as illustrated in Table 3, for N=10 companies and N=1000 companies. Of notice, for a high coupling, which is characteristic of markets for shares in companies in the same industry, more companies does reduce the kurtosis with respect to less companies the profile is similar with the estimated kurtosis value when N=1000 surpassing by far that of N=10, when v1 = 0.2 , this means that turbulence, in this case, is not necessarily reduced by increase in market size in terms of number of companies. The number of companies does, however, affect the synchronization dynamics as we will now show.
| v1 | N =10 | N =1000 |
|---|---|---|
| 0 | 2.1811 | 2.13888 |
| 0.05 | 3.80407 | 2.92959 |
| 0.1 | 4.65971 | 4.67501 |
| 0.15 | 10.628 | 7.36895 |
| 0.2 | 45.201 | 137.744 |
Table 3: Sample kurtosis for different values of v1 , v2 = 0.04 , ε = 0.7 , with the remaining parameters equal to Figure 23.
When dealing with a multi-asset market, the issue of dynamical synchronization is a key problem, in this case, we find a relation between synchronization in assets’ returns, the financial turbulence and the number of companies, with implications for financial diversification. If we calculate the market standard deviation of the financial returns for the N companies at each interaction, we get the series of standard deviations that measure the dispersion of the N companies’ returns at each trading round, the lower the value of this indicator is, the higher is the synchronization in financial fluctuations:

For high coupling, we find that this standard deviation is not only low, which means that we have a high synchronization, it fluctuates in dispersion bands, as exemplified in Figure 25 where the market standard deviation around the mean returns is plotted, for a high coupling zero noise case with 10 companies, to plot this series we used a scatterplot, which makes the fluctuation bands visible, these fluctuation bands increase with the number of companies, as shown in Figure 25 (right), where the number of companies is increased to 100, therefore the market size, in this case, matters since it increases the number of fluctuation bands for the standard deviation of the financial returns around the mean field.
The presence of noise breaks down the bands and increases the standard deviation interval, the resulting dynamics leads to a tension between the global coupling, the underlying chaotic dynamics and the stochastic component, in this way, while the chaotic dynamics with the spatial coupling produces a band structure, with high synchronization, the activation of the stochastic component is incorporated in the market dynamics in a way that produces greater deviations from synchronization, feeding into the chaotic component, in this way, without noise, the high coupling may reduce the effect of diversification on portfolio risk due to the high market synchronization.
While noise might seem to benefit to some degree diversification leading to divergence between the different assets, the nonlinear coupling extends to the noise itself which is also incorporated in the local chaotic dynamics through the speculation impact variable’s mean field coupling and fed back into that mean field’s dynamics, in the case of low noise this leads to a positive relation between synchronization and periods of high volatility risk, indeed, for low values of l, while the stochastic component leads to higher deviations in each trading round between the market dynamics for the different companies, the diversification effect is lost in high volatility periods, as illustrated in Figure 26.

Figure 25: Time series scatterplots of the dynamics of sd(t) , for N =10 (left)
and N =100 (right), 100,000 iterations in each case after 10,000 initial iterations
removed for transients, uniformly randomly chosen initial conditions, 
When l is small there is a skew occurring in trading rounds with high mean field volatility measured by the squared value of the returns mean field, in this way, high volatility and large price jumps tend to occur with low inter-asset dispersion (high interasset synchronization), that is, the market tends become collectively volatile in the high volatility events, reducing the portfolio diversification effect (Figure 26 in the left), on the other hand, as shown in Figure 26 (right), for a high enough value of l, the dynamics is reversed, the higher jumps occur for the cases where there is more inter-asset dispersion, despite the fact that the asset dispersion is low, which means that these jumps occur for higher inter-asset dispersion moments, this is the scenario where some large jumps move the market upwards or downwards with a few stocks as market movers for which the size of the speculation impact on the market is higher, a similar profile is shown in Figure 27, for another parameter setting.

Figure 26: Scatterplots for sv(t) versus the squared value of
the returns mean field, N=100, 100,000 iterations, after 10,000
initial iterations removed for transients, l = 0.001 (left) and
l = 0.05 (right), the randomly chosen initial conditions used
in the left simulation were the same as those used in the right, 
Considering the above results, the stochastic chaos model shows how collective speculative dynamics can lead to macroscopic turbulence, including a time varying synchronization between different company’s stock market returns so that the effects of diversification can be lost in the periods of higher price jumps where the mean value of the logarithmic returns shows the highest jumps, as well as another profile where the noise impact level leads to a few stock movers driving the market’s mean returns, a phenomenon that is linked with differing transaction volumes and thus differentiated size of speculator impact on different company’s shares. The profile depends upon the noise level. However, as is illustrated in Figure 27, while generally characterized by the second profile, the largest jump, which in this case was a market loss of around 0.33 in the logarithmic returns mean field, occurred due to synchronization with a lower dispersion value, which means that the two profiles may coexist and are not mutually exclusive. In both profiles macroscopic losses can occur and lead to high portfolio level losses.

Figure 27: Scatterplots for sv(t) versus the squared value of the returns
mean field, N=100, 100,000 iterations, after 10,000 initial iterations
removed for transients, uniformly randomly chosen initial conditions, 
Discussion and Conclusion
Bachelier’s theory of speculation assumed that speculators trade randomly and independently from each other, averaging out. In the GRW model this assumption and general theory still holds but for a Gaussian distribution associated with the speculation impact on logarithmic returns, leading to a lognormal distribution of prices. In the GRW model, Bachelier’s theory supports a fixed volatility, with the volatility parameter setting the scale for a speculation impact variable as an IID Gaussian noise term affecting logarithmic returns. Instead, financial markets show evidence of power law signatures, nonlinear dependences and even chaos signatures, as well as multifractal scaling, characteristic of some form of chaos induced SOC.
In this work, following Lo’s AMH, we departed from Bachelier’s main assumption that speculators operate independently from each other, addressing speculators as having an adaptive behavior with collective self-correcting dynamics, in this case, we showed that a basic feedback dynamics of speculative trends and market corrective motions incorporated in a cubic map model coupled with a changing volatility variable is enough to lead to the main financial turbulence features, in a single and multiple asset setting.
We showed that, for this adaptive speculative dynamics, the market exhibits different dynamical behaviors, including nonturbulent platykurtic regime and a turbulent leptokurtic regime for a wide parameter range with features of chaos induced SOC with multifractal scaling for the logarithmic returns, the lognormal regime showing up as a transitional regime in the simulated market dynamics for specific parameters.
The turbulence is explained in the model by a distortion of the financial returns versus volatility attractor, which shows a volatility compression for the middle values of the speculation impact variable and a divergence in volatility at the extremes, this distortion coupled with the speculative trend formation and subsequent market corrective dynamics explain the alternation between laminar periods and turbulent periods characterized by high clustering volatility and price jumps.
In the artificial financial market with multiple assets and globally coupled stochastic chaos, we also found that global speculative dynamics are capable of producing macroscopic turbulence with SOC signatures and nontrivial dynamical synchronization patterns with higher volatility periods and price jumps occurring in high synchronization periods as well as possible stock movers driving the market upwards or downwards possibly leading to large portfolio gains or even losses with volatility rising for greater inter-asset dispersion, both these dynamical profiles can occur in a same simulation and both these dynamics will feedback into the local speculative dynamics through the mean field.
More research into artificial financial markets taking advantage of coupled nonlinear maps, connecting complex adaptive financial speculation dynamics with multiple asset types, as well as investor types, is relevant in order to produce possible explanatory frameworks to understand financial risk dynamics and sufficient conditions with which complex turbulent patterns can arise, as well as providing new tools and insights into portfolio management and financial risk management.
REFERENCES
- Bachelier L. Théorie de la spéculation. InAnnales scientifiques de l'École normale supérieure. 1900;17:21-86.
- Mandelbrot BB, Fisher A, Calvet L. A Multifractal Model of Asset Returns. Cowles Foundation Discussion Papers. 1997:1164.
- Mandelbrot BB. The variation of certain speculative prices. InFractals and scaling in finance. Springer. 1997:371-418.
- Mandelbrot BB, Hudson RL. The (Mis)behaviour of Markets: a Fractal View of Risk, Ruin and Reward. Basic Books. 2004.
- Voit J. The Statistical Mechanics of Financial Markets. Springer. 2001.
- Calvet L, Fisher A. Multifractality in asset returns: theory and evidence. Rev Econ Stat. 2002;84(3):381-406.
- Gonçalves CP. Financial Turbulence, Business Cycles and Intrinsic Time in an Artificial Economy. Algor Fin. 2011;1(2):141-156.
- Gonçalves CP. Quantum Financial Economics Risk and Returns. Jour Syst Sci Complex. 2013;26(2):187-200.
- Jiang Z-Q, Xie W-J, Zhou W-X, Sornette D. Multifractal analysis of financial markets: a review. Rep Prog Phys. 2019;82(12):125901.
[Crossref],[Google Scholar],[Pubmed]
- Shao Y-H, X H, Liu Y-L, Xu H-C. Multifractal Behavior of Cryptocurrencies Before and During COVID-19. Fractals. 2021;29(6):2150132.
- Araújo FHA, Fernandes LHS. Multifractal Detrended Fluctuations Analysis for IBOVESPA Assets. Fractals. 2021;29(7):2150183.
[Google Scholar], [Crossref]
- Chen P. A Random Walk or Color Chaos on the Stock Market? Time-Frequency Analysis of S&P Indexes. Stud Nonlinear Dyn Econom. 1996;1(2):87–103.
- Abbaszadeh MR, Nooghabi MJ and Rounaghi MM. Using Lyapunov’s method for analysing of chaotic behaviour on financial time series data: a case study on Tehran stock exchange. NAR. 2020;2(3):297–308.
- Song X, Niu D, and Zhang Y. The Chaotic Attractor Analysis of DJIA Based on Manifold Embedding and Laplacian Eigenmaps. Math Probl Eng. 2016;8087178.
- Vogl M and Roetzel PG. Chaoticity Versus Stochasticity in Financial Markets: Are Daily S&P 500 Return Dynamics Chaotic? Commun Nonlinear Sci Numer. 2022;108:106218.
- Bak P, Tang C, Wiesenfeld K. Self-Organized Criticality: An Explanation of 1/f Noise. Phys Rev Lett. 1987;59(4):381-384.
[Crossref],[Google Scholar],[Pubmed]
- Bak P, Paczuski M. Complexity, contingency, and criticality. Proc Natl Acad Sci.1995;92(15):6680-6696.
[Crossref],[Google Scholar],[Pubmed]
- Girardi-Schappo M. Brain criticality beyond avalanches: open problems and how to approach them. J. Phys. Complex. 2021;2:031003.
- Chang T. Self-organized criticality, multi-fractal spectra, sporadic localized reconnections and intermittent turbulence in the magnetotail. Phys Plasmas. 1999;6(11):4137-4145.
[Crossref], [Google Scholar]
- Handel PH. 1/f Noise Criterion for Chaos in Nonlinear Systems. Noise in Physical Systems and 1/f Fluctuations. IOS Press. 1992:151-157.
- Kaneko K, Tsuda I. Complex Systems: Chaos and Beyond: Chaos and Beyond: A Constructive Approach With Applications in Life Sciences. Springer Science & Business Media. 2001.
- Lo A. The Adaptive Markets Hypothesis. J Portf Manag. 2004;30(5):15-29.
[Crossref], [Google Scholar],
- Palmer RG, Arthur WB, Holland JH, LeBaron B. An artificial stock market. Artif Life Robot. 1999;3(1):27-31.
- Lux T, Marchesi M. Scaling and Criticality in a Stochastic Multiagent Model of a Financial Market. Nature. 1999;397:498-500.
[Crossref], [Google Scholar]
- Farmer JD. Market force, ecology and evolution. Ind Corp Change. 2002;11(5):895-953.
- Schredelseker K, Hauser F. Complexity and Artificial Markets. Springer.2008.
- Kaneko K. Spatiotemporal intermittency in coupled map lattices. Prog Theor Phys. 1985;74(5):1033-1044.
- Kaneko K. Spatiotemporal chaos in one-and two-dimensional coupled map lattices. Physica D. 1989;37(1-3):60-82.
- Kaneko K. Clustering, coding, switching, hierarchical ordering, and control in a network of chaotic elements. Physica D. 1990;41(2):137-172.
[Crossref], [Google Scholar]
- Kaneko K. Globally coupled circle maps. Physica D. 1991;54(1-2):5-19.
[Crossref], [Google Scholar]
- Kaneko K, Ikegami T. Homeochaos: dynamics stability of a symbiotic network with population dynamics and evolving mutation rates. Physica. D. 1992;56(4):406-429.
[Crossref], [Google Scholar]
- Lavin JF, Valle MA, Magner NS. A Network-Based Approach to Study Returns Synchronization of Stocks: The Case of Global Equity Markets. Complexity. 2021;7676457.
[Crossref], [Google Scholar]
- Gonçalves CP. Multifractal Financial Chaos in an Artificial Economy. 2010.
- Frey M, Simiu E. Deterministic and Stochastic Chaos. Comp Stoch Mech. 1993:195-216.
- Puu T. Nonlinear Economic Dynamics. Springer. 1997.
- LR Gorjão, Hassana G, Kurths J, Witthauta D. MFDFA: Efficient multifractal detrended fluctuation analysis in python. Comp Phys Commun. 2022;273:108254.
[Crossref], [Google Scholar]
Citation: Gonçalves CP (2022) Coupled Stochastic Chaos and Multifractal Turbulence in an Artificial Financial Market. Int J Swarm Evol Comput. 11:261
Copyright: © 2022 Gonçalves CP. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.