Journal of Bacteriology & Parasitology

Analytics of Contagion in Inhomogeneous Random Social Networks

Hurd TR^* Department of Mathematics, McMaster University, Hamilton, Canada
^*Correspondence: Hurd TR, Department of Mathematics, McMaster University, Hamilton, Canada, Email:

Received: 12-Feb-2021 Published: 05-Mar-2021, DOI: 10.35248/2155-9597.21.12.391

Description

The IRSN framework of \cite{HURD2020} has the following basic elements and assumptions many variations of the basic template are possible.

1. Individuals are distinguished by their type T ∈ [M]:={1,2...,M} and by their disease status. As in conventional SIR ordinary differential equation (SIR-ODE) models, disease status is represented by compartments including “susceptible (S)”, “infective (I)” and others. The framework focusses on tracking the random subset S(t|T) of type T susceptible individuals at the end of day t, and similarly I(t|T),...,etc.

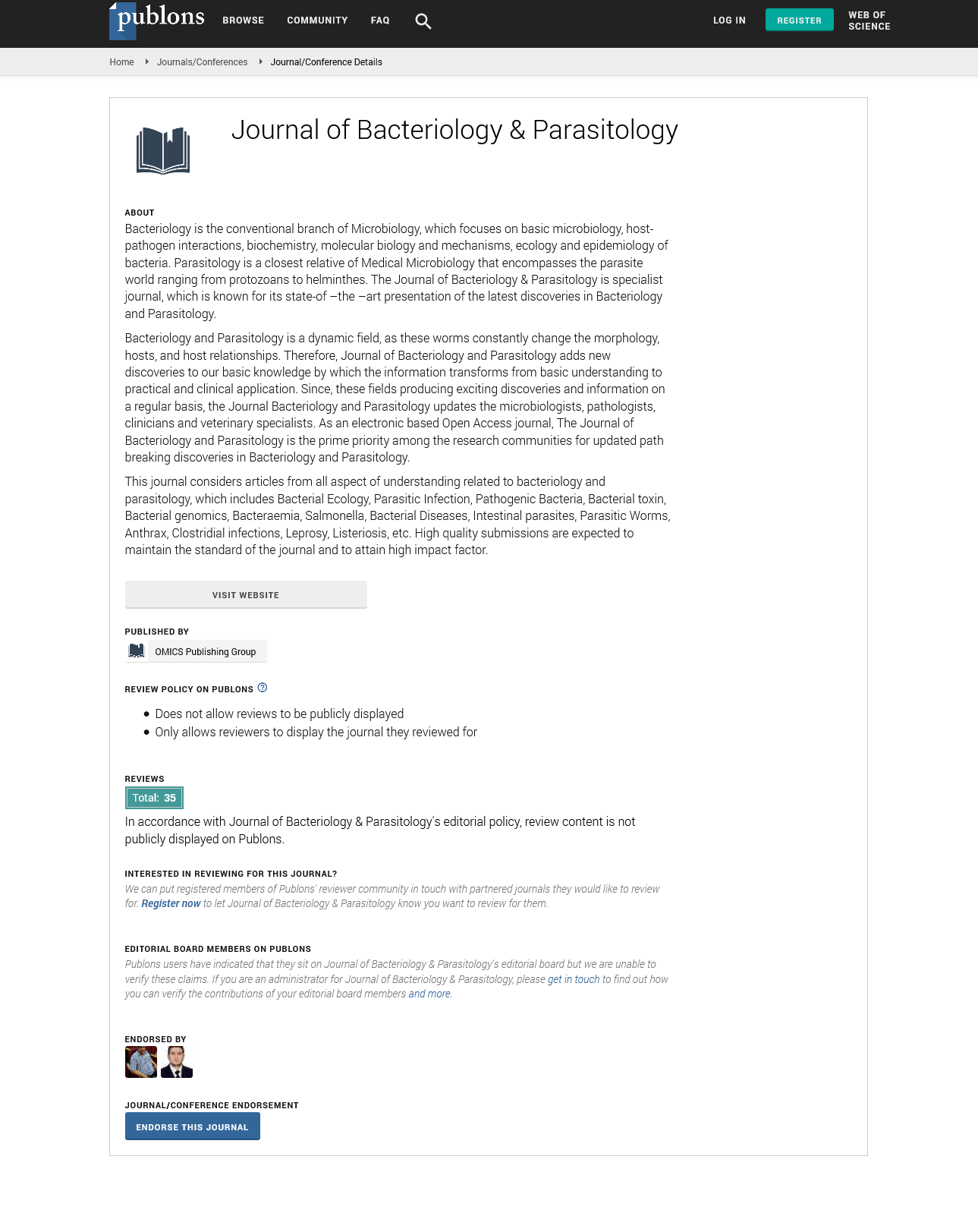
2. An individual v ∈ S (t|T) will become infected (or “exposed”) by the end of day t 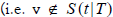if the threshold condition 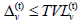holds, where 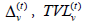are the immune buffer of v and the total viral load accumulated by v from all social encounters with infectives on day t. Between-compartment transmission follows a discrete-time analogue of usual assumptions made in SIRODE models.

3. The social network structure on the population is assumed to be an inhomogeneous random graph that is fixed over time, with connection probabilities calibrated to existing demographic data. A person’s Total Viral Load (TVL) each day is the sum of random viral doses received through their infectious contacts, which are a random subset of their social contacts.

4. Random elements are updated daily, and include immune buffers, daily social encounters, viral doses exchanged during infectious contacts. Agent-based methods are used to motivate the specific IRSN rules that determine their joint probability distributions over time.

The key element of the IRSN is the threshold infection assumption, which encodes a dose-response mechanism. The main technical result of the IRSN model, called the mixed infection cascade mapping, provides recursive equations for the various compartment probabilities s(t |T) := P(v∈S(t |T)),i(t | T) := P(v∈I(t | T)) etc. proved under a certain large N or “mean-field” type approximation. 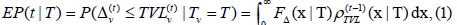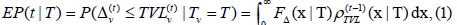At its core is a formula for the conditional exposure probabilityIs the prescribed distribution function of a type T buffer; the density of TVL is given by an inverse Fourier transform 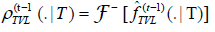where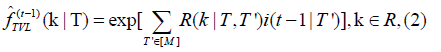

Here R is a constant [M, M] matrix-valued function that encodes average total viral load encountered by type T susceptibles per type T’ infective. Validating the threshold infection assumption requires investigating models of in-host viral dynamics as reviewed in Perelson and Ke, an active area of immunology [2]. A consequence of (1) is that in the specific setting where immune buffers are exponentially distributed random variables, the IRSN model becomes a discrete time approximation of the analogous continuous time ODE model [1]. Thus the IRSN framework provides a direct derivation of any SIR-ODE model from a more fundamental agent-based model. However, immune buffers may take other distributions, in some cases leading to discernible deviations from SIR-ODE models. In a typical computer implementation using the discrete Fourier transform with grid size Nfft ∼2⁸, computational time of the mixed infection cascade mapping is dominated by computing (1). This amounts to O ( Nfft × M²) flops and O ( Nfft × M) exponentiations per discrete time step, which is in practice similar to the speed of the comparable SIR-ODE model.

Several important contagion effects are characteristic of real epidemics and agent-based models such as the IRSN, but do not fit easily into conventional well-mixed SIR-ODE models. The so-called frailty bias or susceptibility bias refers to the fact that during an outbreak, the average characteristics of the susceptible population evolve, because frail individuals are likely to succumb to the disease before robust individuals. The effect of social bubbles, where people seek to reduce their exposure probability by restricting their daily contacts to a small group, is similarly captured easily in agentbased models such as the IRSN, but not in ODE models.

Incorporating more refined data into IRSN models is facilitated by two operations that increase the resolving power of the framework. Disaggregation, that is, building a model that splits types into subtypes with the aim to resolve finer features, is desirable when data indicates that these variations are significant, and can lead to better predictions of focussed policy interventions. Aggregation creates a new model by combining two or more submodels, for example, building a model for Canada by merging models for each of its provinces and territories. This requires only the additional information of the cross-border traffic. Both ways to extend models are compatible with the architecture of the IRSN framework. If we consider IRSNs as multilayer networks, as reviewed in Kivelä et al. by allowing edge variables to become multidimensional, the key elements still fit together, and in particular equations similar to (1), (2) continue to hold [3]. The extra dimensions may represent a diversity of features, such as different viral strains, the tissue within the host where infection occurs, or the different settings such as schools, workspaces and households where infectious contacts may occur.

The IRSN framework provides a concise and flexible microscopic foundation that underpins, explains and can replace, SIR-ODE models. Designing IRSN models requires one to adopt the viewpoints of different types of people, as in agent-based modelling. They can be built starting from any SIR template for disease status compartments, then combined with behavioural assumptions for individuals that can be validated by similar criteria used for agentbased models. In versions of the IRSN model where the large N approximation is valid, the resultant mixed infection cascade mapping is easy to program, fast to compute even with thousands of types, providing a bridge in complexity between microscopic agent-based models and macroscopic SIR-ODE models.

REFERENCES

1. Hurd TR. Covid-19: Analytics of contagion on inhomogeneous random social networks. Infect Dis Model. 2020;6(1):75-90.
2. Perelson AS, Ke R. Mechanistic modelling of SARS-COV-2 and other infectious diseases and the effects of therapeutics. Clin Pharmacol Ther. 2020;41(2):9-17.
3. Kivelä M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA. Multilayer networks. J Complex Networks. 2014;2(3):203–271.