Journal of Clinical Research & Bioethics

Advancing Dose-Finding Trials: A Review of the Modified Huber Loss Function for Continual Reassessment Methods

Fangfang Jiang^1,2, Emine O. Bayman^1,2 and Gideon K. D. Zamba^{1,3* 1}Department of Biostatistics, University of Iowa, Iowa City, IA, United States of America
²Department of Biostatistics, Clinical Trials Statistical and Data Management Center, University of Iowa, Iowa City, IA, United States of America
³The Holden Comprehensive Cancer Center, Iowa City, IA, United States of America
^*Correspondence: Gideon K. D. Zamba, Department of Biostatistics, University of Iowa, Iowa City, IA, United States of America, Email:

Received: 13-Jun-2024, Manuscript No. JCRB-24-25992; Editor assigned: 17-Jun-2024, Pre QC No. JCRB-24-25992 (PQ); Reviewed: 01-Jul-2024, QC No. JCRB-24-25992 (R); Revised: 09-Jul-2024, Manuscript No. JCRB-24-25992 (R); Published: 18-Jul-2024, DOI: 10.35248/2155-9627.24.S20.001

Introduction

Dose-Finding (DF) trials, in Phase I clinical trials, have been fraught with challenges in striking the balance between inducing response/activity and minimizing toxicity. The Traditional Escalation Rule (TER), also known as the “3+3” design, while easy to implement, has been criticized for ignoring accumulated information on z dose-toxicity. Continual Reassessment Methods (CRM), which use a sequential update scheme, address the shortcomings of TER by assuming a structure on a dose-toxicity curve and employing a Bayesian framework to re-evaluate the dose-toxicity profile and make decisions as the trial observations accumulate.

The standard CRM creates an identifiability dilemma as it focuses only on the point estimate of the mean posterior probability of Dose-Limiting Toxicity (DLT) at dose d_i, i.e., π_β(d_i), while disregarding the uncertainties about the distribution of π_β(d_i).

Literature Review

As the need to improve clinical trial methods to ensure a quick evaluation of the Maximum Tolerated Dose (MTD) becomes urgent, adapting DF trials to new contingencies is equally important. To address this issue, Zhang et al., proposed a decision making framework based on loss functions, specifically the Generalized Modified Huber Loss Function (GMHLF) in a fully Bayesian decision-making on DF trials with fewer patients than standard methods [1].

Role of loss functions

Although loss functions are critical for determining DLT in CRMs, they have not yet received enough attention in clinical trials. Several loss functions, such as absolute error loss and quadratic loss, have been commonly used in early-phase clinical trials. These loss functions penalize deviations from the target more severely as the deviation increases. This feature can lead to dose decisions being heavily influenced by extreme departures from a target dose. Toxicity Interval Loss Function (TILF) has been used in fully Bayesian decision-based CRM. Rather than penalizing deviations from a target dose level (i.e, considering the influence of extreme departures), TILF assigns different penalties based on pre-defined toxicity probability intervals for π_β(d_i) [2,3]. It has been documented that TILF can lead to unstable estimates of DLT, especially when doses are concentrated at a single level [4].

The paper by Zhang et al., emphasizes the importance of loss functions and seeks to use the Huber Loss Function (HLF) in fully Bayesian decision-based CRM to better manage extreme departures from a target dose in DF trials. HLF applies a quadratic loss function for data points in the neighborhood of the target dose and transitions to an absolute loss beyond this vicinity [5]. The authors retain these properties and assign more steep penalties for extreme departures. This is especially critical in early-phase clinical trials where the sample size is often small, and a few extreme actions must be carefully considered due to their significant impact on dose determination.

Additionally, Zhang et al., discuss the GMHLF, which allows for unequal penalties for under-dosing and overdosing in DF trials. It should be noted that it is critical for clinicians to understand these methods as GMHLF requires a pre-specified tolerance level k to control the neighborhood around the target dose level. In the absence of clinical expert opinions, Zhang et al., recommend 1.5sd ≤ k 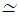2sd as an appropriate tolerance level, where sd is the standard deviation of the standardized dose candidates. If the dose candidates do not reflect the entire picture of dose-toxicity profile, are we truly advancing the CRMs, or are we stuck in a methodological stalemate by introducing tolerance level k? In the simulations to determine the optimal choices of k, Zhang et al., propose three scenarios for the distribution of true probabilities of DLT at dose d_ibut the range between the minimum probability and the maximum probability is at least 0.4. This ignores the impact of concentrated dose levels that may have close DLT levels. Thus, the choices of k determined by their simulations might not perform well under other dose-toxicity conditions. Clearly, determining the acceptable neighborhood of the target dose level is an unfinished but important task in GMHLF.

Performance evaluation of GMHLF

The authors consider three different dose-toxicity profiles to evaluate the efficacy and accuracy of their approach: Oneparameter logistic model, the two-parameter logistic model, and the one-parameter power model [6,7]. The target DLT for both the one-and two-parameter logistic models is set at 30% and five dose candidates are evaluated. In contrast, for the one-parameter power model, the target DLT is set at 25% and six dose candidates are assessed. The maximum sample size is set at 36, and the patients enter the trial in groups of three. Under these settings, six competing DF algorithms are compared:

1. TER

2. Point estimate from standard CRM

3. Decision rule based on TILF

4. Bayesian Optimal Interval Design (BOIN) [8]

5. Optimal design in Paoletti, O’Quigley, and Maccario [9]

6. Method based on GMHLF.

BOIN uses a Bayesian decision-theoretic framework and aims to minimize the probability of incorrect decisions to escalate or deescalate the dose. Optimal design is a theoretical benchmark of no practical use that provides a reference upper bound to the performance of any realistic method. An algorithm for implementing GMHLF can be found in Zhang et al., [1]. Four operating characteristics are used to evaluate the performance of algorithms:

1. The proportion of patients treated at MTD

2. The proportion of correct recommendations of MTD

3. The average sample size needed for the trial to recommend the MTD, and, specific to TER

4. The proportion of patients developing DLT.

Under both one and two parameter logistic models, across all the scenarios, the TER fails to locate the MTD as it tends to be lured to the less toxic dose level than the MTD. Zhang et al., refer to this as a “trigger-happy” tendency. Since their study requires that the doses enter the trial starting from the lowest dose level, we are uncertain whether this tendency is caused by the order of entry. But such requirement is understandable as DF trials typically start with the lowest dose to minimize exposure to toxic doses. The same tendency occurs sometimes with TILF. However, GMHLF provides a promising performance. It selects the true MTDs with higher accuracy and assigns a higher proportion of patients to MTDs consistently, which is satisfactory in terms of operating characteristics. Besides, GMHLF performs as well as, if not better than, CRM choices based on point estimates.

Under a one-parameter power model, TER is still unable to find the MTD, while GMHLF tends to perform as well as BOIN with fewer sample sizes on average. This efficiency plays an important role in clinical trials, such as cancer trials, where accrual, retention, and compliance are at stake.

But can we take a leaf out of our book and focus only on the operating characteristics of the algorithms at the true MTD? What if GMHLF appears to accurately recommend a true MTD on average, but the patient is at high risk of being assigned to a more toxic dose level sometimes? More investigations on the robustness are still needed.

Zhang et al., also apply GMHLF to data on the gemcitabine trial which originally used TER in the Phase I clinical trial. Like the simulations, GMHLF requires fewer patients to determine the MTD than TER. In this trial, GMHLF was able to cut the number of patients to half. TILF shows a “trigger-happy” tendency. The poor performance of BOIN reveals the limitations of TER-like algorithms in finding MTDs as they do not have the flexibility to jump or readjust to a working model when there are too many candidate doses [10].

Discussion

Allowing a random starting dose, especially when the dose spectrum has multiple dose levels, seems to be a good choice for testing the robustness of GMHLF. Will this require more patients or less to locate MTDs? Will it increase the chances of a patient being assigned to an MTD? Will it inadvertently expose patients to more toxic dose levels? These issues present an attractive direction for future research. Besides, the authors provide formulas for asymmetric GMHLFs which treat the under-dosing and overdosing unequally. However, the simulations only involve symmetric GMHLFs while the performance of asymmetric GMHLFs is unknown and requires further study.

It is undoubtedly a challenge to make findings based on such complex statistical methods understandable to non-statistician practitioners. It would be beneficial to develop an interactive, user-friendly R Shiny App, in addition to the R software package mentioned by the authors, to raise the benefits of this new approach in clinical applications.

Conclusion

GMHLF not only selects the MTD consistently but also reduces the average number of patients needed to reach the MTD. This helps minimize the exposure of patients to futile/harmful dose levels. By modifying the tolerance level and penalty pattern over under-dosing and overdosing, Zhang et al., offer flexibility to GMHLF to be fine-tuned to the nature of the drug being tested. In conclusion, what is the best way to locate the MTD? The authors suggest considering various loss functions or implementing multiple DF algorithms jointly before settling on MTD. The challenge, therefore, switches to effectively synthesizing the results of different algorithms. Balancing these results requires careful consideration of each algorithm's objective and contribution to the overall decision making.

References

1. Zhang L, Bayman EO, Zamba KD. A modified Huber loss function for continual reassessment methods in clinical trials. Seq Anal. 2024;43(1):28-48.

   [Crossref] [Google Scholar]

2. Ji Y, Li Y, Nebiyou Bekele B. Dose-finding in phase I clinical trials based on toxicity probability intervals. Clin Trials. 2007;4(3):235-244.

   [Crossref] [Google Scholar] [Pubmed]  

3. Neuenschwander B, Branson M, Gsponer T. Critical aspects of the Bayesian approach to phase I cancer trials. Stat Med. 2008;27(13):2420-2439.

   [Crossref] [Google Scholar] [Pubmed]  

4. Paoletti X, Kramar A. A comparison of model choices for the continual reassessment method in phase I cancer trials. Stat Med. 2009;28(24):3012-3028.

   [Crossref] [Google Scholar] [Pubmed]  

5. Huber PJ. Robust Estimation of a Location Parameter. Ann Math Statist. 1964;35(1):73-101.

   [Crossref] [Google Scholar]

6. Berry SM, Carlin BP, Lee JJ, Muller P. Bayesian adaptive methods for clinical trials. CRC press. 2010.

   [Google Scholar]

7. Lee SM, Cheung YK. Model calibration in the continual reassessment method. Clin Trials. 2009;6(3):227-238.

   [Crossref] [Google Scholar] [Pubmed]

8. Liu S, Yuan Y. Bayesian optimal interval designs for phase I clinical trials. J R Stat Soc., C: Appl Stat. 2015:507-523.

   [Crossref] [Google Scholar]

9. Paoletti X, O'Quigley J, Maccario J. Design efficiency in dose finding studies. Comput Stat Data Anal. 2004;45(2):197-214.

   [Crossref] [Google Scholar]  

10. Abbruzzese JL, Grunewald R, Weeks EA, Gravel D, Adams T, Nowak B, et al. A phase I clinical, plasma, and cellular pharmacology study of gemcitabine. J Clin Oncol. 1991;9(3):491-498.

    [Crossref] [Google Scholar] [Pubmed]