International Journal of Swarm Intelligence and Evolutionary Computation

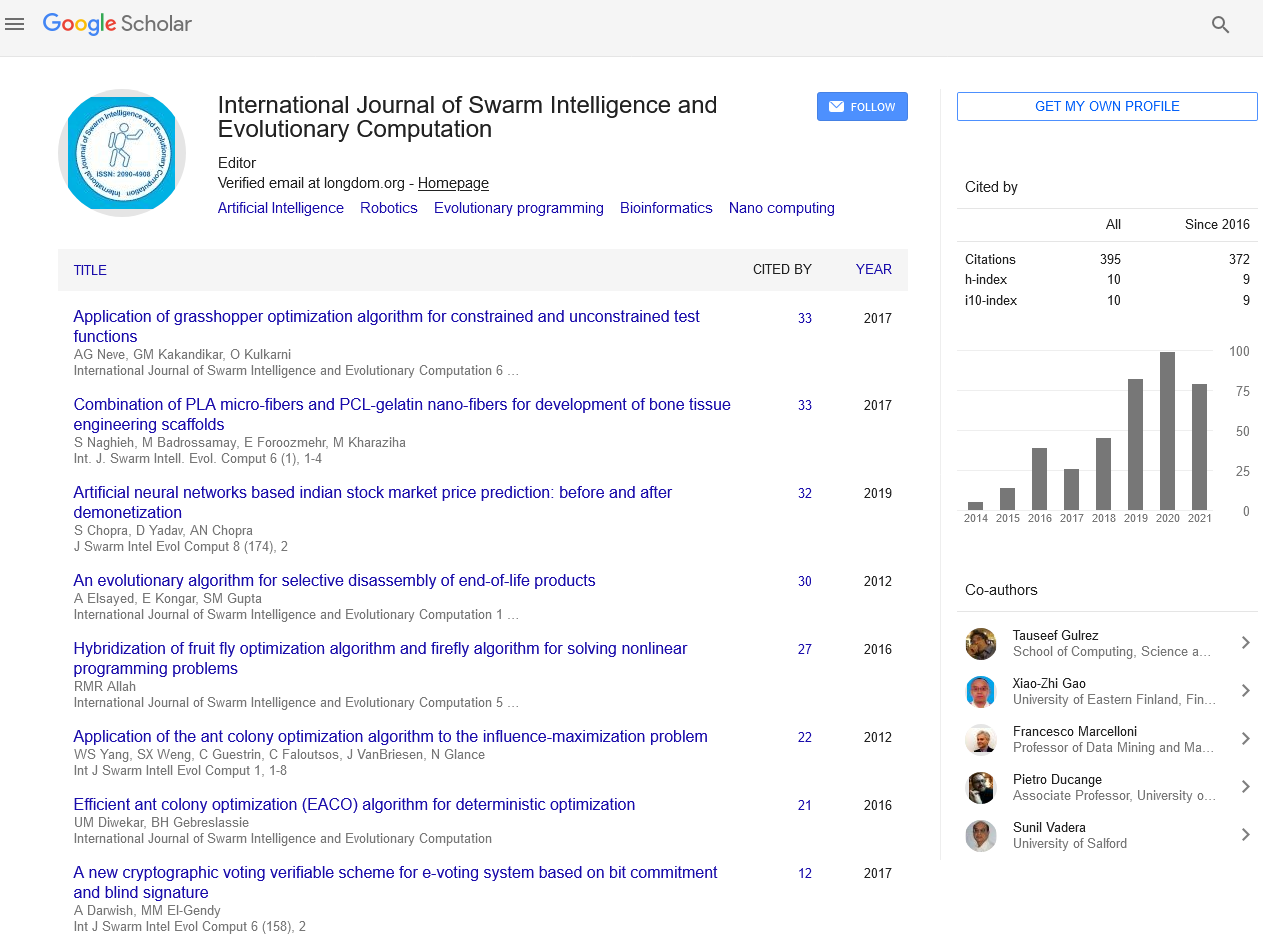
Abstract

Stochastic Chaotic Network Vector Fields

Carlos Pedro Gonçalves*

The present work addresses stochastic chaotic dynamics in network vector fields described by coupled stochastic differential equations, expanding on stochastic chaos in coupled map lattices. We study the example of a network with local coupling and ring topology with the vector field dynamics at each node being described by locally coupled stochastic differential equations given by the stochastic Lorenz system, the resulting local dynamics, mean field dynamics and synchronization
patterns are researched for different coupling strengths and network sizes, showing the presence of a relation to the Lorenz chaotic attractor as well as multifractal scaling in the field dynamics and multifractal phase transitions. The relevance of the results for the research on the synergetics of complex systems and networked  computation is addressed.

Published Date: 2025-02-24; Received Date: 2025-01-22